基于二维激光测距仪的三维模型配准研究

梅 强，吴怀宇

（武汉科技大学 信息科学与工程学院，湖北 武汉 430081）

在移动机器人领域，环境建模与运动规划都是机器人实现智能性的具体表现。其中环境建模是一个非常复杂和耗时的问题。因为这项研究涉及一些基本的科学问题。而本文将介绍自主移动机器人的控制和二维激光测距仪结合电机云台生成三维点云，然后通过多方位的三维点云在同一个坐标系统中建立一个大致的场景。

激光测距仪雷达以其精度高、测距速度、快获取信息直观等优点在军事、民用和航空等领域得到了越来越多的应用。有些团队用二维激光测距仪建立三维环境。如zhao[1]等人使用了两个二维测距仪来获取三维数据。一个激光扫描仪水平安装，另一个垂直安装。通过当前的机器人机器人位姿将其转换为一个三维点。还有一些团队跟本文采取方法一样。Unchter和Surmann[2]，蔡自兴和邹小兵[3]采用精度转动云台与2-D扫描的激激光测距传感器，设计并实现了非结构化环境下移动机器人识别感知系统，该系统可分析地面的平坦性和判断移动机器人的障碍区域和可行区域，为移动机器人导航过程中的路径规划与环境建模提供支持。

在三维重建过程中，数据配准自动化程度决定了三维重建过程的自动化程度，数据配准结果也在很大程度上决定了三维模型重建精度。数据配准过程分为：粗配准、精度配准和全局配准[4]。最常见的粗配准方法是基于物体的球谐函数、高阶矩不变量。基于随机采样的几何哈希技术的配准方法也十分常见。将这种算法应用于三维数据配准中，并考虑到了误差的对速度影响。利用了仿射不变量来约束候选样本数量，极大地加快了配准的速度。

1 三维点云信息获取

在测量距离时，通过测量激光从发出到接受所经历的时间来计算出物体到激光测距仪的距离。本文采用二维激光配合旋转电机的方法获取三维空间点云数据，实现三维场景构建。通过10 s左右的时间内完成一次从下到上，从右到左的完整扫描，获取竖直方向100°区域、平面方向180°区域内的一组大约361×500的三维激光点云数据。

如图1所示，为三维激光测距系统的参数坐标关系图，ρ作为激光发射点到被测物体的距离；θ为扫描方向的水平偏向角度；φ为云台旋转角度，从而得到以云台旋转轴为坐标中心的三维激光参数（ρ，θ，φ）。再通过参数标定获取平台参数（a，b，z）然后由式（1）计算机器人当前位姿场景数据（x，y，z）通过里程计获取当前位姿Px，Py，Pθ，由式（2）计算得到三维场景的全（X，Y，Z）[5]。如图2所示，为二维激光和云台结合的三维点阵效果图。

图1 三维激光测距系统参数坐标关系图Fig.1 Coordinate diagram of 3D laser ranging system

图2 三维点阵Fig.2 3D point cloud array

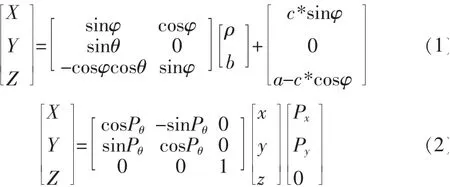
2 多平面特征提取

机抽样一致性RANSAC算法并不是用所有的初始值去估计模型参数的算法，而是满足可行条件的尽量少的初始数据。并使用一致数据集去扩大它，这是一种寻找模型去拟合数据的思想。

2.1 拟合直线段端点的定权算法

本文提出的算法直接拟合平面所属的拟合直线段集合中每个拟合直线段的端点数据进行拟合平面参数。可将拟合直线段端点的定权问题转化到二维空间中进行讨论。并认为同一条扫描线中共面的扫描点的精度相同且相互独立，根据间接平差法的原理并考虑本文所采用的直线拟合公式，可知拟合直线方程公式中两系数的协因数阵为

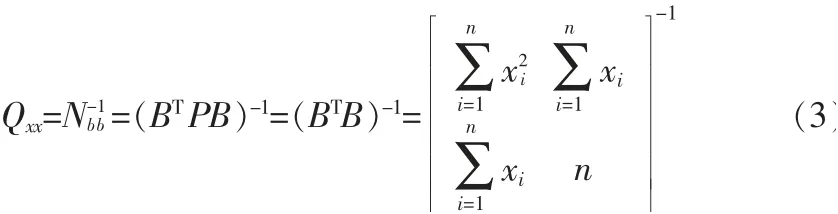
拟合直线段端点的坐标为拟合直线段系数的参数，写成矩阵形式如式（4）：

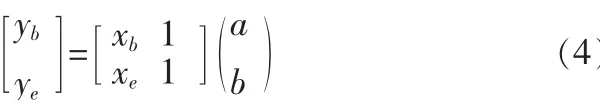
其中，（xe，xb）（xb，yb）分别为拟合直线段的两段点。根据误差传播律，向量（yb，ye）T的协因数阵为：

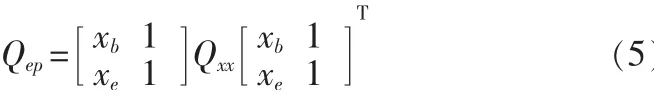
就拟合直线段集合而言，各条拟合直线段可认为相互独立。因此，整个拟合直线段集合集中所有拟合直线段点的协因数阵（此矩阵对角线上元素不为零，其余元素为零）为：

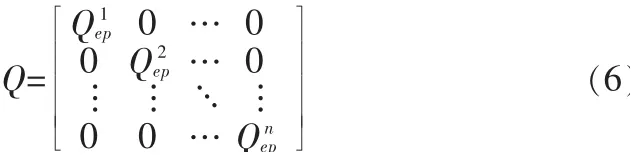
式中：Qiep为拟合直线段集合中第i条拟合段两端点的协因数阵；n为拟合直线段集合中拟合直线段的数量。采用分块矩阵逆算法对Q阵求逆，即可得到所需的权阵。

2.2 利用拟合直线段端点计算拟合平面

一个三维平面通过两种方式就可模拟出来。第一种可以用不共线的3个三维点（p1，p2，p3∈R3）计算出穿过这3个点的平面ax+by+cz+d=0的参数；第2种是通过一个三维点和通过这个点的平面法向量（p1，n且‖n‖=1，p1，n∈R3）也可以计算出这个平面的参数。通过以下步骤来提取平面[8]：

1）在初始点云中随机选择3个点，直接计算平面ax+by+cz=0，然后再计算点云至生成平面的距离di=|axi+byi+czi+d|。

2）选择阈值t，若di≤ε则认为是内点，统计得出此平面内点的个数。

3）如果这个平面的内点数超过了一个作者设计的极致数（比如50个点），那么就确定这个平面是存在的且记录下来。再用同样的方法迭代其他的平面。如果这个平面内点不能超过极致数，这个平面就不存在且不记录下来。同样再重复第一步骤迭代提取平面。

阈值的选择很重要，在判断内点的时候如果选择过小的阈值会放弃选择的内点，而选择过大的阈值则可能将异常点误判为内点。

3 ICP算法配准

Besl和Mikay所介绍的迭代最近点法ICP是从测量点集中确认对应的最近点点集后，运用和所提出的严密解算过程重新计算最近点点集；迭代计算直到目标函数值不变化，停止迭代过程。Besl和Mikay用以下7个参数向量作为旋转和平移的表示方法：

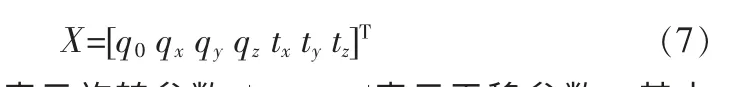
[q0，qx，qy，qz]表示旋转参数，tx，ty，tz」表示平移参数。其中选择参数满足约束条件为：根据迭代初值X0，计算新点集Pi

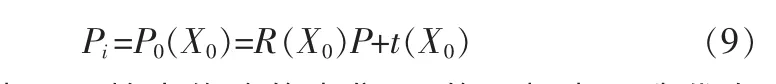
其中Pi表示原始未修改的点集，Pi的下标表示迭代次数，参数向量X的初始值为：

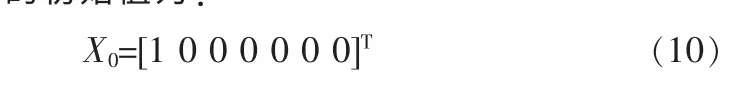
ICP处理过程如下：

1）由点集Pk中的点，搜索曲面S上相应最近点点集Prk；

2）计算两个点集的重心位置坐标，并进行点集中心化生成新的点集，并确定正定矩阵N。

3）根据[16]计算最大特征向量等价于残差平方和最小时旋转矩阵R。其中旋转矩阵R：

4）在旋转矩阵R被确定后，由平移向量t仅仅是两个点集的重心差异，可以通过两个坐标中的重心点和旋转矩阵确定。

4）通过迭代的思想用参数向量Xk+1、R、t生成一个新的点集Rk+1；

5）当距离平方和的变化小于预设的阈值τ时就停止迭代，停止迭代的判断准则为fk－fk+1＜τ。

4 四点算法配准

在ICP算法的基础之上加入限制约束条件。对ICP算法计算前随机提取有规律的四点进行迭代。使全局配准具有较好的鲁棒性，在原始数据有外点，噪声较大时也能获得较好的初值。对应点搜索步骤如下：

1）点集中随机选择一个平面上的4个点a，b，c，d计算交点e，以及比例和距离d1＝‖a－b‖；d2＝‖c－d‖，保证鲁棒性a，b，c，d 4点两两的距离大于一定值，如图3所示。

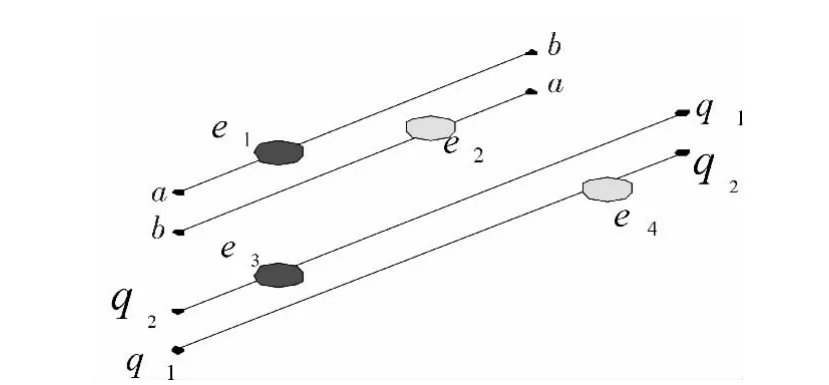
图3 获取四点距离及其比例Fig.3 The proportions and distances of four points

2）在Q点集中。找出所有可能的点对，使距离分别等于d1和d2，并将这对集合分别保存在集合A和B中，其中qa，qb，qc，qd分别是a，b，c，d点可能的对应点，如图4所示。

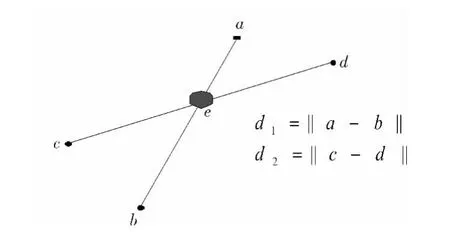
图4 可能存在的对应点Fig.4 The corresponding possible point

3）分别计算集合和中的每一对点映射相交点e1＝qa+r1（qa－qd），e2＝qc+r2（qc－qd），如图5所示。

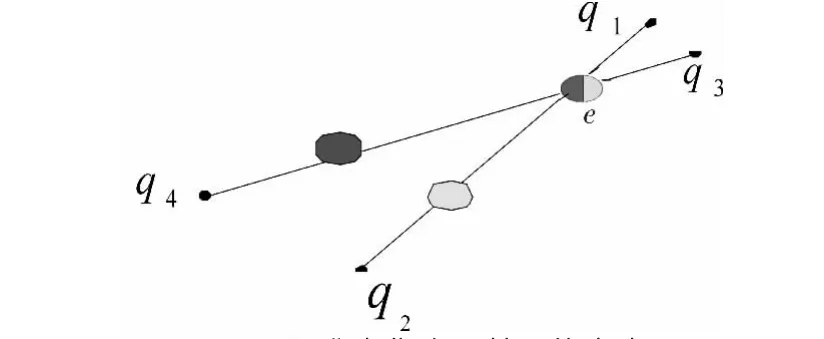
图5 配准点集合及其可能交点Fig.5 Registering collection and possible intersections

4）如果e1≈e2，则qa，qb，qc，qd对应点就确定了。其中需找相同交点可以采用KD－Tree来加速。

5 实验结果与分析

本文开发了配准软件的图形界面，基于OpenGL技术进行三维点云数据的人机交互显示，使用C++开发语言。选择使用的VCGlibrary开源函数库，提供了大量的三维数据处理的函数模块，给算法实现减少了很多编码工作量，使得研究工作能更多地专注于算法思想上。

本文将四点算法和传统进行比较分析。如图6（a）（c），随着高斯噪音和异常点比例的加强，评估误差（马尔科夫误差）会有明显不一样。在低高斯噪音和低异常点比例的良好条件下二者算法的配准精确度相差不多。而在高噪音和高异常点比例的不利条件下时四点算法精确度明显好于RANSAC。如图6（b）随着重叠区域的比例变小，四点算法的精确度也优于传统RANSAC。同时在计算的速度上面四点算法也优于传统RANSAC，如图6（d）。

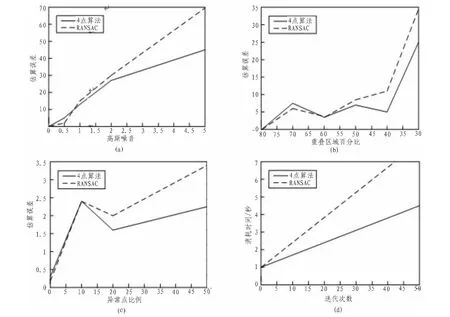
图6 （a，b，c，d）四点算法和传统算法指标参数比较Fig.6 Parameters comparsion of four points algoritnm and traditional RANSAC algorithm

下面是经过展现的效果图。图7是通过提取平面特征后再经过四点算法配准后得到的三维配准图。

图7（a）为两个激光扫描图初始配准图；7（b）图为经过5次迭代后的配准图；图7（c）为经过25次配准迭代后的配准图。

图7 配准实验图Fig.7 The registration rendering

6 结束语

通过三维激光和转动云台得到三维点阵，并用四点算法进行粗配准。经实验验证，该算法计算量小且能正确的配准三维模型。完全满足移动机器人实时性和准确性的要求。

本文只考虑了两视角间三维点云数据的配准问题，并没有考虑多视角间的全局数据配准。而后续工作将可以基于这个方向发展。可以加入ICP算法精确配准加以完善。可以根据文献[6－7]实现根据不同的数据集，自动选择采样方法，以增加配准的自动化程度和鲁棒性。

[1]Zhao H，Shibasaki R.Reconstructing textured CAD model of urban environment using vechile-borne laser range scanners and line cameras[J].Lecture Notes in Computer Science，2001，34（5）：284－295.

[2]Nuchter A，Surman H，Hertzberg J.Automatic model refinement for 3D reconstruction with mobile robots[C]//Proceedings of the Fourth International Conference on 3－D Digital Imaging and Modeling，2003：394－401.

[3]邹小兵，蔡自兴，于金霞.基于激光测距的移动机器人3－D环境感知系统设计[J].高技术通讯，2005，15（9）：38－43.ZOU Xiao-bing，CAI Zi-xing，YU Jin-xia.Mobile robot based on laser ranging 3－D context-aware system design[J].Chinese High Technology Letters，2005，15（9）：38－43.

[4]Cecilia.C and Chen.R.Segmentation and registration for 3D modeling of large-scale urban scenes[D].City University of New York：Chen.R，2007.

[5]陈杭.移动机器人三维环境建模与自主运动规划[D].大连：大连理工大学，2009.

[6]Gelfand N.，Ikemoto L.，Rusinkiewicz S，et al.Geometrically stable sampling for the ICP algorithm[C].Proceedings of the Fourth International Conference on 3D Digital Imaging and Modeling，2003：260－267.

[7]Lee B U，Kim C M，Park R H.An orientation reliability matrix for The iterative closest point algorithm[J].IEEE Tansactions on PAMI，2000，22（10）：1205－1208.

[8]赵录刚，吴成柯.基于随机抽样一致性的多平面区域检测算法[J].计算机应用，2008，28（r2）：154－157.ZHAO Lu-gang，WU Cheng-ke.Multi－plane region detection algorithm based on random sampling consistency[J].Journal of Computer Applications，2008，28（2）：154－157.