GPS天线相位中心变化精确检测试验研究

陈 涛 胡志刚 李 陶

1)地壳运动监测工程研究中心，北京 100036

2)中国地震局地质研究所，北京 100029

3)武汉大学卫星导航定位技术研究中心，武汉 430072

0 引言

全球定位系统(Global Positioning System，简写为GPS)的基本工作原理是测量已知位置的卫星到地面点之间的距离，然后通过解算多颗卫星的数据得到地面点的精确坐标。目前，GPS观测数据已被广泛应用于地球动力学研究和高精度地壳形变监测(刘经南等，1999)。在进行高精度GPS观测时，地面观测点的天线相位中心(天线接收卫星信号的电气中心)与天线机械几何中心并不完全一致，因此需要进行天线相位中心校正。目前，绝大多数天线相位中心的校正参数都是由国际导航定位服务(International GNSS Service，简写为IGS)或者第三方提供。在公布的天线改正模型中，相同型号同批次出厂的GPS接收机天线相位的中心偏差水平分量基本一致。不同型号的接收机天线差别较大，水平方向的误差达mm级，垂直分量的误差甚至为cm级(李晓波等，2012)。因此，天线相位中心稳定性检测已被列为中国大陆构造环境监测网络(简称陆态网络)流动观测前必须检验的项目之一。

天线相位中心对测量结果的影响可分为天线相位中心偏差(Phase Center Offset，简写为PCO)和天线相位中心变化(Phase Center Variations，简写为PCV)两部分。其中，PCO是指天线相位中心与几何中心之间的偏差。虽然理论上天线电气中心应与天线的几何中心一致，但由于制造水平、信号入射方向、高度角等原因，天线相位中心与几何中心之间会存在一定偏差。PCV是指天线平均相位中心与瞬时相位中心之间的变化，其主要受信号仰角影响，而非信号的方位角。几乎所有的高精度GPS测量天线，其相位中心方向图都是关于方位角对称。除此之外，接收机天线整流罩以及不同载波工作频率也会对天线相位中心变化产生一定影响(国家测绘局，1995)。

任何特定天线的PCO都具有一定的稳定性，即呈现系统误差的特性。相比之下，PCV的精确校正较为复杂，目前使用的主要方法包括微波暗室测量法(Rothacher，2001;高伟，2004)，相对现场定位法(Schmid et al.，2005)和测量机器人标定法(张成军，2010;Dach et al.，2011)。1994年提出的微波暗室测量法能够精确测定天线的相位中心，但需建设专门的微波暗室，且设备昂贵复杂，不易维护，测量费用较高，难于推广。相对现场定位法是通过多台接收机联合同步观测，得到相对PCV参数。由于参考天线相对于被测天线的PCV较小，可以对其拟合求得卫星在各高度角时的PCV值。实验证明，经PCV改正后的双差载波相位数据的标准偏差＜1cm(李晓波等，2012)。从1996年6月30日起，IGS各个分析中心开始使用相对相位中心改正模型(Aloi et al.，2005)。但事实上参考天线的绝对PCV并不是0，并且还存在现场操作条件制约等缺陷，因此该方法计算得到的PCV往往会产生系统误差。Schmitz等(2002)讨论了相对定位技术的弊端，提出利用自动测量机器人的绝对现场校准来进行天线相位中心标定。

基于精密机器人的现场标定法的优点非常明显，首先该方法可以给出绝对标定值，消除了参考天线的相位中心影响，同时，有效减弱了多路径效应，观测值覆盖整个天线半球，可获得从0°～90°高度角范围的PCV，且考虑了PCV随方位角的变化。而且，精密机器人方法可以重复观测数千次，最大限度地消除了多路径效应，可以更精确地定义相位中心的位置，这对于确定高分辨率和高精确度的PCV模型非常必要。同时，利用精密机器人完成1次标定仅需几个小时，且其测量的相位中心变化值与微波暗室测量结果相吻合，能够达到1mm的精度(Montenbruck et al.，2009)。自2011年11月6日之后，IGS开始使用由波茨坦地学中心(Helmholtz-Centre Potsdam-German Research Centre for Geosciences，简写为GFZ)和慕尼黑工业大学(Technische Universitaet München，简写为TUM)提供的绝对天线相位中心改正模型来代替相对相位中心改正模型。截止目前，IGS所提供的最新的天线相位中心改正模型中，有大约70%的接收机天线都是由测量机器人校准后得到(李晓波等，2012)。

1 方法模型

1.1 相位中心改正模型

天线相位中心的改正模型包括PCO改正和PCV改正两部分(李晓波等，2012)，本文主要参照胡志刚等(2011)提出的天线相位中心改正模型，设天线相位偏差PCO的矢量为a，卫星与接收机之间的矢量为r0，那么天线相位中心的改正模型可表述为

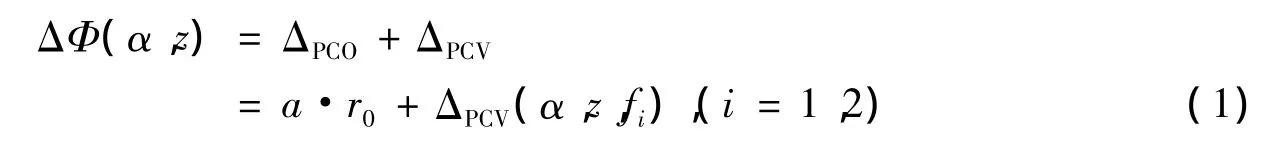
式(1)中，α，z，fi分别为方位角、天顶距或高度角以及所接收的载波信号频率，ΔPCV(α，z，fi)为与方位角、高度角和频率有关的改正函数。

利用公式(1)，自由选取PCO矢量，并保证与其对应的PCV满足自洽关系，即可实现瞬时相位中心到天线参考点的相位伪距近似改正。

1.2 PCV计算方法

PCV计算方法一般都采用一个相对于天线参考系在水平方向和垂直方向都连续的周期函数来模拟与卫星方位角和高度角相关的PCV。例如，Rothacher等(1995，2001)使用球谐函数来模拟PCV，该方法虽然具备较好的物理意义，但是缺点是所需要估计的系数较多，计算量较大。另一种方法是利用分段线性函数来描述与方位角和高度角有关的PCV(Schmid et al.，2005;胡志刚等，2011)，即假设PCV模型由不同的网格点构成，每个格网均由4个待求PCV点组成。如图1所示，PCV在格网待求点A，B具有相同的高度角(z1)和不同的方位角(α1和α2)，同样C，D也具有相同的高度角(z2)和不同的方位角(α1和α2);而A，D两点具有不同的高度角(z1和z2)和相同的方位角(α1)，同样B，C两点也具有不同的高度角(z1和z2)和相同的方位角(α2)。假设观测时刻的高度角(z)和方位角(α)均位于ABCD所限定的网格内，则P点的PCV值可由线性内插的方法得到:

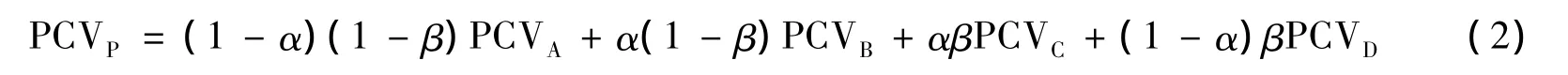
其中，α =(a－a1)/(a2－a1)，β =(z－z1)/(z2－z1)。

前人研究表明，采用球谐函数法和分段线性函数这2种方法计算得到的PCV值差别并不大，但分段线性函数法相对更易于实现(Schmid et al.，2005;胡志刚等，2011)。因此，本研究采用5°×5°网格点进行线性分段计算，当建立天线参考系后，假设公式(1)中的PCO相对于天线参考系是固定不变的，则PCO的值可以通过参数估算得出，随后将其作为强约束条件，计算得到PCV。

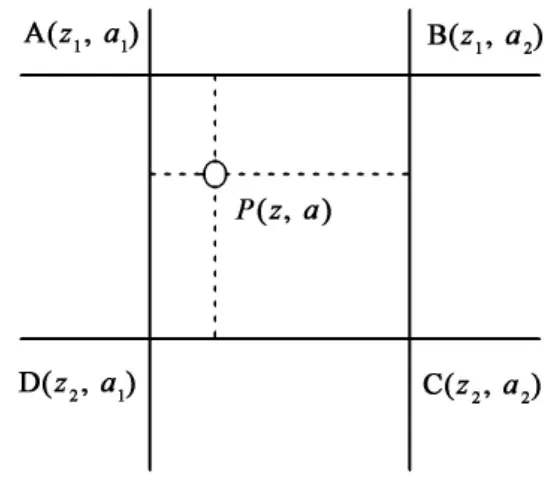
图1 PCV网格点线性插值示意图(据胡志刚等，2011)Fig.1 Schematic diagram of PCV grids linear interpolation(after HU Zhi-gang et al.，2011).

2 试验研究实例

2011年，在陆态网络的建设实施中，地壳运动监测工程研究中心引进日本发那科(FANUC)公司生产的FANUC LR Mate 200iC型自动测量机器人，与中国科学院沈阳自动化研究所和武汉大学卫星导航定位技术研究中心合作，开展了基于自动测量机器人的GPS天线相位中心变化精确检测试验研究。

2.1 场地设置及测量机器人安装

FANUC LR Mate 200iC型自动测量机器人由伺服电机驱动轴和机械手腕共同组成机构部件。如图2a所示，机械手腕部分作为机器臂，手腕的接合部称为轴杆或关节。从基座底部向上的最初的3轴(J1，J2，J3)称为基本轴，分别由几个直动轴和旋转轴构成，主要用于实现较大幅度的水平、俯仰和翻滚动作。机器臂上端的3轴(J4，J5，J6)称为机械腕轴，用于实现小幅度的姿态调整。测量机器人工作时，由基本轴驱动机械腕轴对安装在机器臂顶端的执行器进行姿态调整，如进行扭转、上下摆动、左右摆动等。

为满足试验研究的高精度要求，选取武汉大学卫星导航定位技术研究中心作为试验基地，按照陆态网络连续基准站观测墩的建设要求，修建了2个短基线观测墩，用于安装GPS观测天线和待测天线。其中，一个观测墩内浇筑专用的测量机器人预埋件，另一个观测墩内则浇筑天线预埋件。完成建设后的测量机器人如图2b所示。

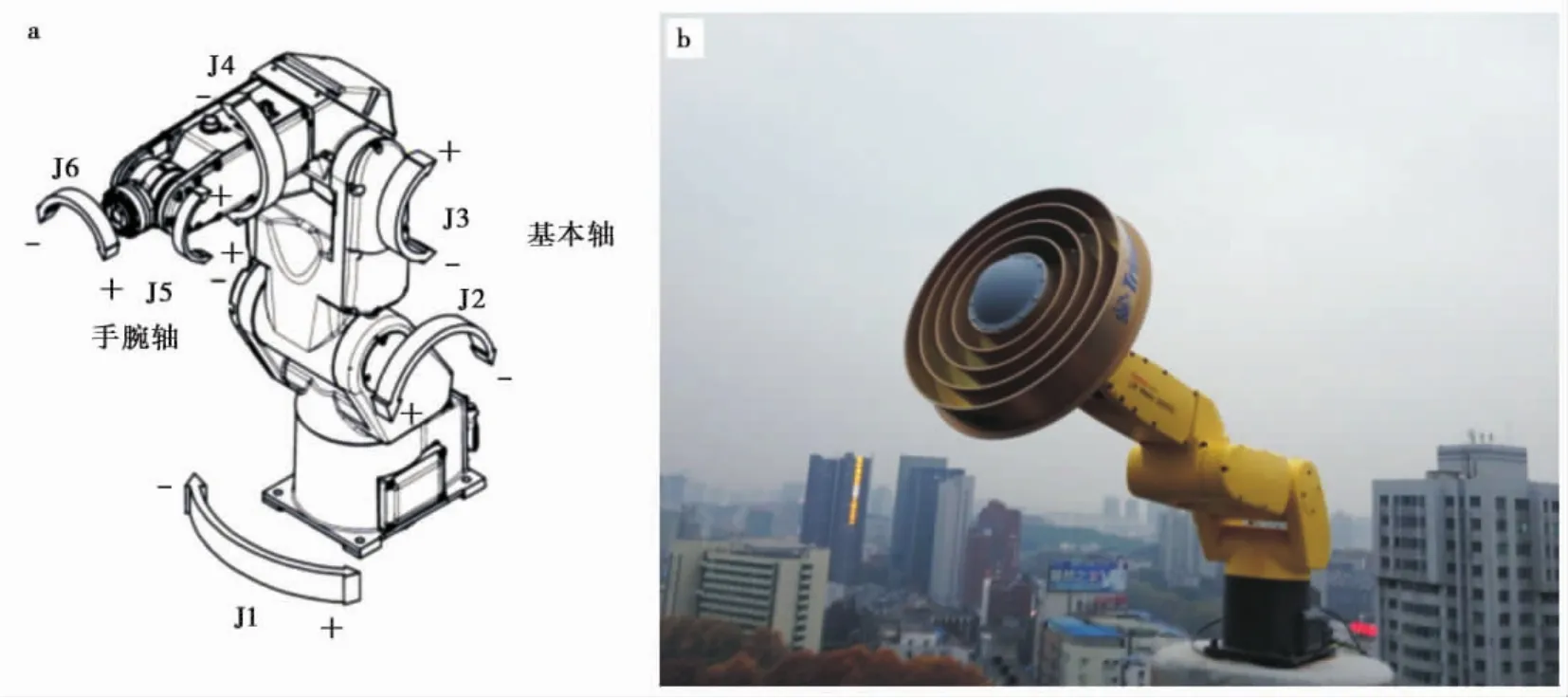
图2 测量机器人组成构件示意图及现场照片Fig.2 Component of the survey robot and the site photo.

2.2 控制软件

中国科学院沈阳自动化所为测量机器人专门编制了控制程序，图3即为控制软件的控制端操作界面。软件实现了对机器人交互式操作，包括数据通讯、状态初始化、静止姿态设计、运动轨迹设计、实时状态显示和结果输出等功能。按照程序设计的步骤，实际测量时天线从仰角90°开始，以5°为间隔逐渐降低，其中在每个仰角高度，方位角以5°为间隔旋转一周。同时，设定机器人从一个状态运动到另一个状态用时1s，在每个停留位置上观测4s。根据上述流程，可计算出实现一个完整的测试流程所需的总时间为(90/5+1)×(360/5+1)×(1+4)=6 935s，约合2h。

2.3 数据质量

多路径误差是高精度标定天线相位中心变化的重要影响因素之一，严重的多路径误差会导致相位观测数据产生数mm甚至cm级的误差，这直接影响到天线相位中心标定的精度。为了检验多路径效应带来的误差，分别采用Trimble Zephyr Model II大地测量型天线和Trimble TRM59800型Choking扼流圈天线进行测试。图4a是Trimble Zephyr ModelⅡ型天线采集时段内所有卫星观测数据处理后的多路径误差统计结果。该图表明所有卫星的多路径误差统计值都＞0.3m，最大值达0.78m，L1和L2上的伪距多路径误差平均值约为0.47m和0.40m。与此形成鲜明对比，图4b是Trimble TRM59800型Choking扼流圈天线的计算结果。从图中可以看到，大部分卫星的多路径误差值＜0.3m，且L1和L2上的伪距多路径误差平均值为0.32m和0.29m，显著地减小了多路径效应带来的误差。因此，本试验研究在进行天线相位中心精确标定时，应尽量使用扼流圈天线，以减小多路径效应的影响。

在测试中，选用2套Trimble NetR8型GNSS接收机及配套的Trimble TRM59800型Choking天线，其中一台置于基站观测墩上，另一台待测天线放置于精密机器臂末端。设置的数据采样率为1Hz，1个观测流程时长约合2h，最终可以得到的待测天线数据覆盖情况。如图5所示，除边缘部分数据覆盖较少外，GPS观测数据覆盖了天线绝大部分区域。需要注意的是，由于测量机器人运动速度较快，而GPS星座相对于接收机变化较慢，因此会导致部分观测数据呈独立的非同心圆形展布。

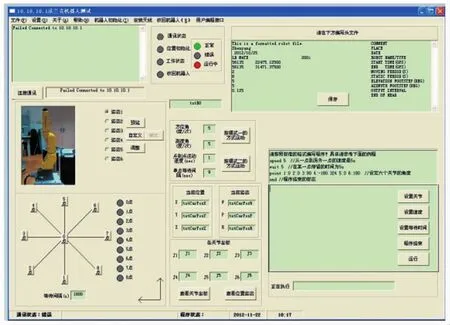
图3 控制软件操作界面Fig.3 The screen capture of the control console.

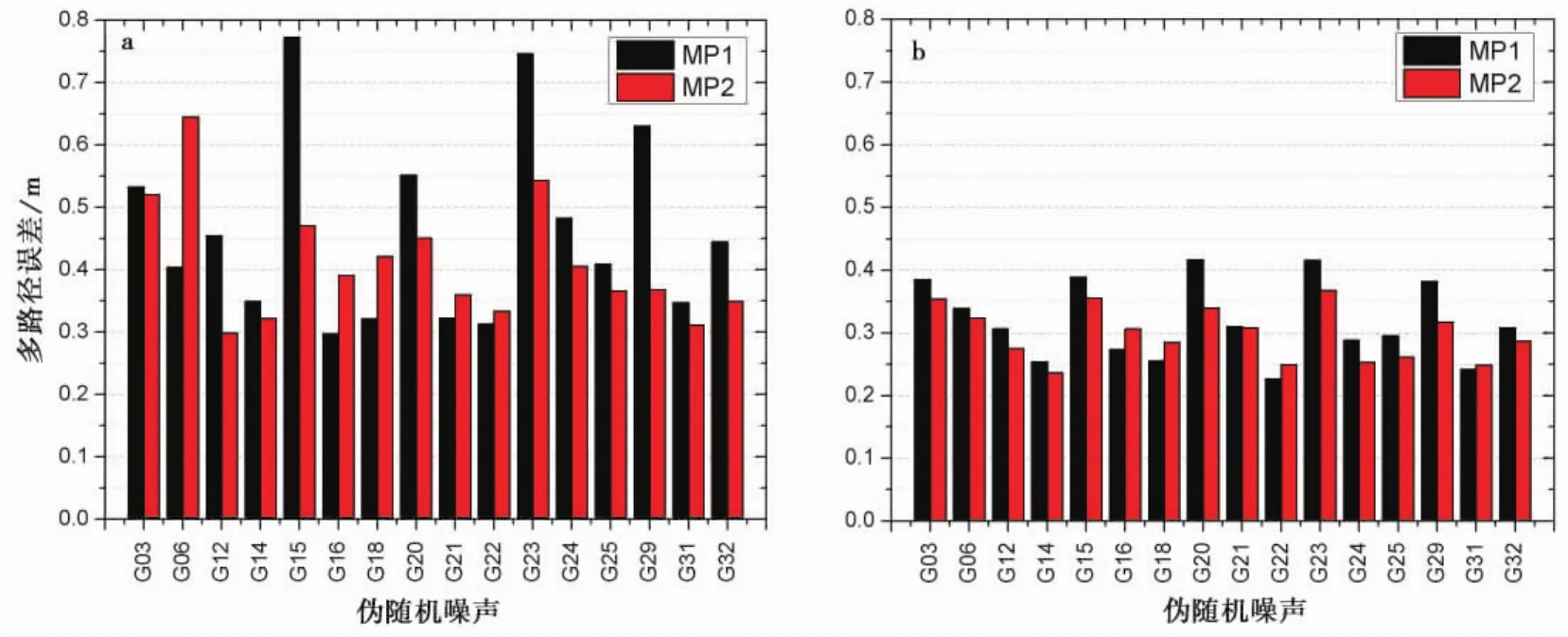
图4 多路径误差Fig.4 Multipath effect comparison of the different antenna.

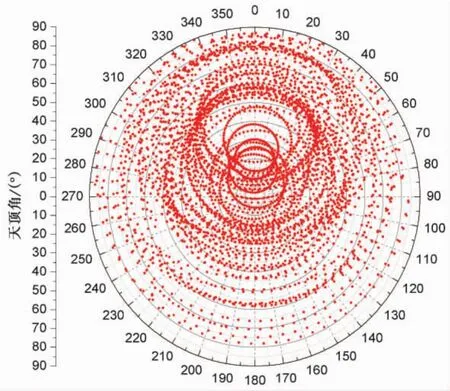
图5 待测天线观测数据覆盖情况Fig.5 Observation data coverage of the tested antenna.

2.4 解算结果

为了尽可能地减小多路径效应影响和后续比较的方便，选用天线校正参数已知的 Trimble TRM59800型Choking天线作为待测试验天线。校正参数由德国GEO++公司提供，并由IGS分析中心推荐，其标称精度为1mm，与微波暗示检定精度相当。将本次试验研究中基于自动测量机器人采集的一个完整检测流程(约合2h)的观测数据，按公式(1)建立函数模型，计算得到的天线相位中心改正数，如表1所示。计算结果表明，测量机器人法得到的天线相位中心与Geo++给出的校正参数偏差在平面方向约为2mm，高程方向约为3mm，平面精度略好于高程。其中，L1Geo++、L2Geo++分别代表Geo++提供的L1和L2载波频率上的改正参数，L1Robot、L2Robot分别代表本研究中计算得到的L1和L2载波频率上的改正参数，ΔL1、ΔL2则分别代表2种方法得到的改正参数之差。

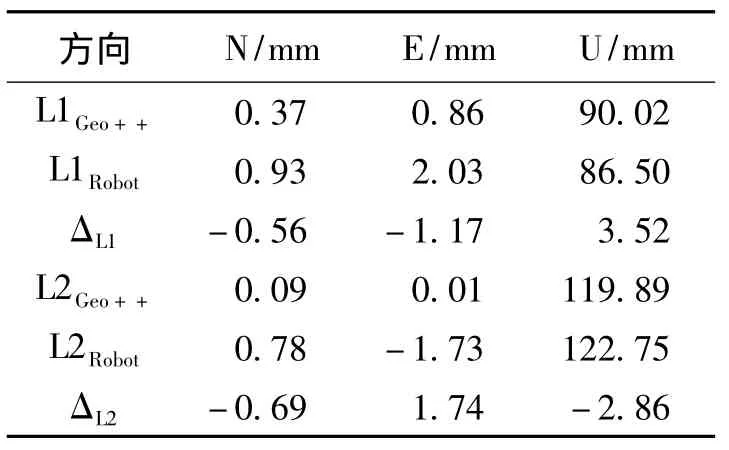
表1 绝对天线相位解算结果Table 1 Comparison of the estimated value and provided value by Geo++

3 结论与展望

随着GPS技术越来越广泛的应用于地球动力学研究和高精度地壳形变监测，对GPS数据处理的精度要求也相应越来越高，而天线相位中心校正参数对提高GPS观测数据精度的重要性不言而喻。本研究对基于精密机器人的GPS绝对天线相位检定标定方法进行了试验研究，获得了平面约2mm、高程约3mm的天线相位偏差修正值。结果表明，基于自动测量机器人的天线相位中心精密检校系统已经建立，当前中国GPS观测所使用的天线校正模型大都由国外机构提供的现状将逐步得以改善。同时，该系统也可用于中国自主研发的北斗卫星导航系统的天线相位中心精密标定。

本文解算的绝对天线相位中心校正参数与IGS推荐的校正参数之间尚存在一定的差异，分析其原因可能是由于观测数据分布并不均匀，也可能是由于研究中仅进行了单个观测周期的试验，在2h内所观测的卫星数量及空间分布范围有限，从而影响了最终结果的准确度。在后续工作中，将进行多次重复观测试验，继续进行分析研究。

高伟.2004.GPS高程测量的理论与方法研究［D］:［学位论文］.武汉:武汉大学.

GAO Wei.2004.Research of the principle and method of the GPS elevation survey ［D］.Dissertation paper.Wuhan University，Wuhan(in Chinese).

国家测绘局.1995.GPS测量型接收机检定规程(CH8O16－95)［M］.北京:测绘出版社.

State Bureau of Surveying and Mapping.1995.Specification for Check off and Test of GPS Receiver of Surveying model(CH8016－95)［M］.Publishing House of Surveying and Mapping，Beijing(in Chinese).

胡志刚，赵齐乐，郭靖，等.2011.GPS天线相位中心校正对星载低轨卫星精密定轨的影响研究［J］.测绘学报，40(增刊):34—38.

HU Zhi-gang，ZHAO Qi-le，GUO Jing，et al.2011.Research on impact of GPS phase center variation on precise orbit determination of low orbit satellite［J］.Acta Geodaetica et Cartographic Sinica，40(suppl):34—38(in Chinese).

李晓波，王小亚，任金卫.2012.GNSS天线相位中心偏差与变化精确标定方法研究［J］.天文学进展，30(4):501—517.

LI Xiao-bo，WANG Xiao-ya，REN Jin-wei，et al.2012.Research on calibration methods of GNSS antenna phase center offsets and variations［J］.Progress in Astronomy，30(4):501—517(in Chinese).

刘经南，陈俊勇，张燕平，等.1999.GPS广域差分定位原理与方法［M］.北京:测绘出版社.

LIU Jing-nan，CHEN Jun-yong，ZHANG Yan-ping，et al.1999.Wider Area Differential Theory and Method ［M］.Publishing House of Surveying and Mapping，Beijing(in Chinese).

张成军.2010.基于测量机器人的GPS天线相位中心影响检测法［J］.测绘通报，(3):7—9.

ZHANG Cheng-jun.2010.Calibration of influence of GPS antenna phase center based on robot［J］.Bulletin of Surveying and Mapping，(3):7—9(in Chinese).

Aloi D N，Rusek A，Oakley B A.2005.A relative technique for characterization of PCV error of large aperture antennas using GPS data［J］.IEEE Transactions on Instrumentation and Measurements，54(5):1820—1832.

Dach R，Schmid R，Schmitz M，et al.2011.Improved antenna phase center models for GLONASS［J］.GPS Solutions，15(1):49—65.

Montenbruck O，Garcia-Fernandez M，Yoon Y，et al.2009.Antenna phase center calibration for precise positioning of LEO satellites［J］.GPS Solutions，13(1):23—34.

Rothacher M，Schaer S，Mervart L，et al.1995.Determination of antenna phase center variations using GPS data［C］.Proceedings of the IGS Workshop，Potsdam.

Rothacher M.2001.Comparison of absolute and relative antenna phase center variations［J］.GPS Solutions，4(4):55—60.

Schmitz M，Wübbena G，Boettcher G.2002.Tests of phase center variations of various GPS antennas，and some results［J］.GPS Solutions，6(1 －2):18—27.

Schmid R，Mader G，Herring T.2005.From relative to absolute antenna phase center corrections［C］.In:Celebrating a Decade of the International GPS Service:Workshop and Symposium 2004，Proceedings:209—221.