MAX-MOS自适应抖动缓冲算法研究

来振宇，王翾

(中国传媒大学广播电视数字化教育部工程研究中心，北京 100024)

MAX-MOS自适应抖动缓冲算法研究

来振宇，王翾

(中国传媒大学广播电视数字化教育部工程研究中心，北京 100024)

抖动是影响VoIP服务质量的一个重要因素。VoIP系统通常通过设置抖动缓冲区来尽可能的减小抖动带来的影响。本文采用帕累托分布对网络延时进行建模，利用E-Model方法计算当前MOS值，通过搜索延时与丢包之间的良好折衷设置缓冲区的大小，从而自适应地获得MOS值的提升。实验表明，该算法在各种实验网络状况下均可以有效的提高VoIP系统服务质量。

VoIP;E-Model;MOS;自适应抖动缓冲

1 介绍

VoIP(IP语音)技术逐渐普及、发展迅猛，在当今的通信市场中占有的份额日趋增长［1］。但基于IP网络传输平台的VoIP不能提供可靠的服务质量一直是制约其发展的瓶颈［2］。抖动(jitter)是网络传输所引入的一个对VoIP话音通信质量产生很大影响的因素。通常我们通过在接收端设置抖动缓冲区来处理抖动。抖动缓冲区能够有效的吸收抖动，降低在接收端产生的丢包率，其性能直接影响着VoIP的语言质量。

目前缓冲算法基本上分为两大类:固定缓冲算法和自适应抖动缓冲算法。固定缓冲算法结构简单、易于实现，但也存在着不能适应网络状况变化的缺点。自适应抖动缓冲算法能够根据网络状况自适应调整缓冲区大小，具有较好的网络自适应性。本文主要研究自适应抖动缓冲算法。文献［3］提出了四种自适应抖动缓冲算法:指数平均、快速指数平均、最小延时、尖峰检测，这四种算法均未与感知语音质量关联起来。文献［4］采用E-Model方法预测语音质量，但只考虑了网络随机丢包，忽略了突发丢包模式。文献［5］也提出了一种基于语音质量预测的自适应算法，同时加入了突发丢包模式，但其参数估计所用历史数据窗为固定大小，灵活性不高。

本文提出了一种基于ITU(International Telecommunication Union，国际电联)在 G.107 建议书［6］中定义的E-Model方法的自适应抖动缓冲算法，该算法采用帕累托分布为网络延时进行建模，根据当前的网络状况自适应的设置缓冲区的大小以得到最大的MOS(Mean Opinion Score)。实验结果表明，本文算法能够在丢包率和延时之间取得较好的平衡，从而使VoIP达到当前网络状况下的最优服务质量。

2 基于E-Model的MAX-MOS自适应抖动缓冲算法

2.1 E-Model方法

G.107中写到［6］:现代网络的复杂性要求规划多个传输参数，对于这些参数，不仅要单独考虑，还要考虑它们的组合效应。由“经验丰富的网络专家进行评测”可以做到这点，但更希望能够提出一种系统性的方法，例如使用计算机模型。G.107提出了一种标量质量等级值——传输性能等级系数R。R值的计算综合考虑了室内噪声、电路噪声、丢包率、延时、抖动、扬声器回声等多个网络损伤因素对话音质量的影响，它正比于总的通话质量变化，取值范围为从0到100。R值的计算公式如下:

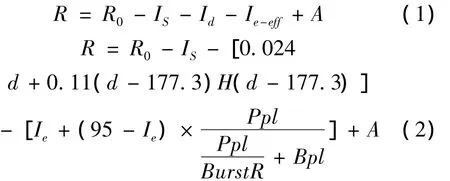
其中d为网络单向延时，是网络传输延时dnet和抖动缓冲延时dbuff之和;丢包率Ppl为网络丢包率Pplnet和接收端抖动缓冲丢包率Pplbuff之和;BurstR为突发比，取值范围为1～2。H(d)的定义如下:

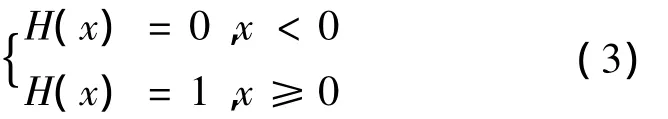
在G.107的附件中，提供了由R值向MOS值转换的公式。R值可以最终转化为平均主观值MOS，转化公式如下:

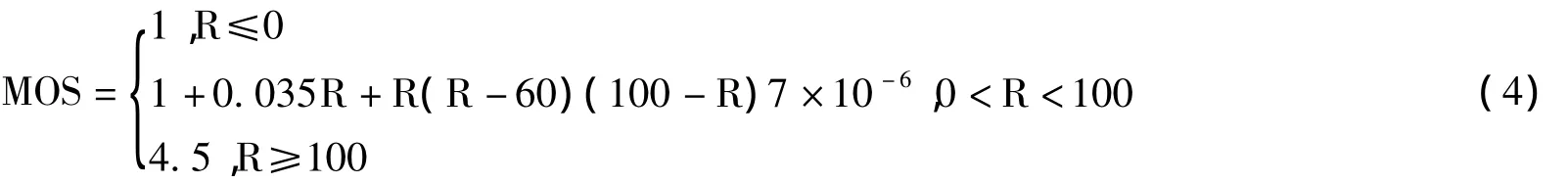
MOS值与R值的关系如图1所示:

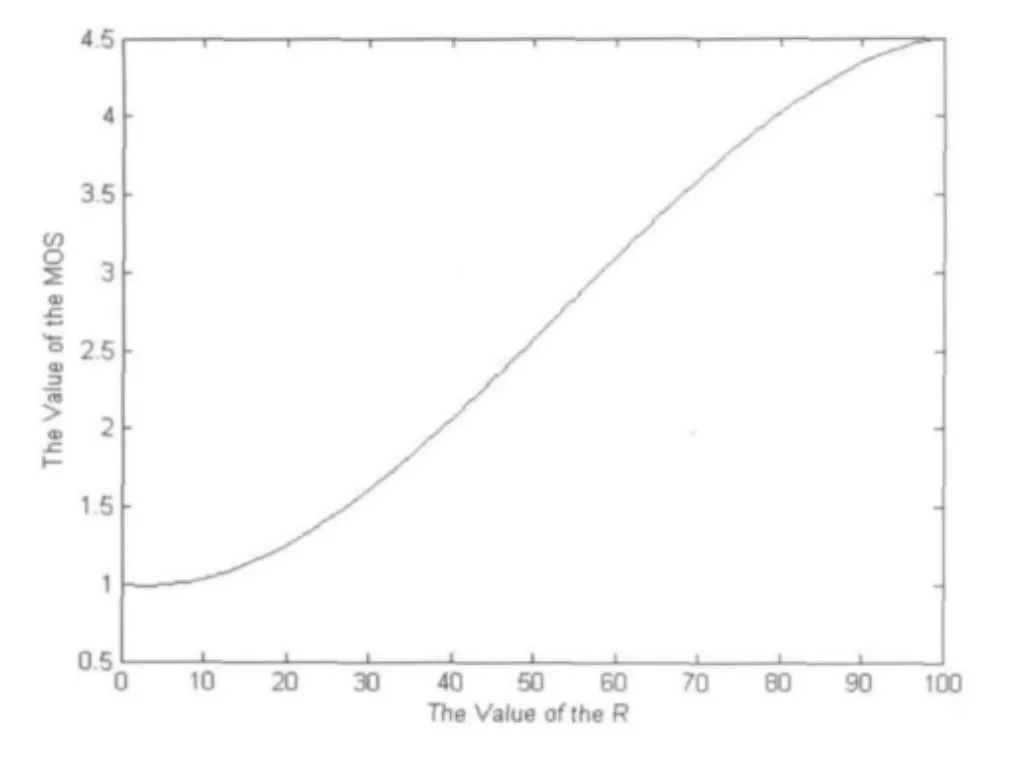
图1MOS值与R值关系

以音频编码 G.711为例，G.113［7］中对该编码方式给出的Ie、Bpl的建议值分别为0和25. 1;R0=100，IS=6.8，A=0。公式(2)可以简化为:

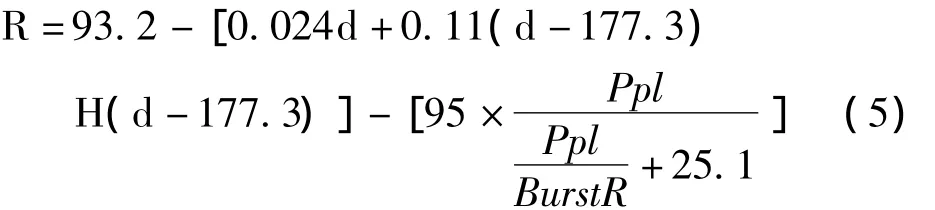
公式(5)中，dnet可以通过时间戳、包序号直接测量得到;dbuff为缓冲区的大小。Pplnet可在接收端直接测得，Pplbuff需要通过对延时d进行分布建模，通过延时分布的累积函数预测得到。

2.2 帕累托延时分布建模

在文献［8］中指出，对于VoIP流量的延时分布，帕累托分布具有较高的匹配度，且相比其他模型形式较为简单。文献［12］中更指出，在任何网络环境下，帕累托分布都是最适合单向延时分布的计算机模型。帕累托分布的累积分布函数如下:

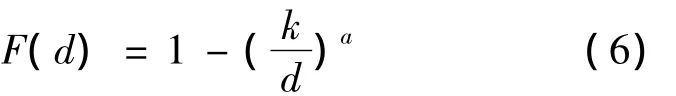
帕累托分布的两个参数k，a可由n个网络延时数据估计得到，估算公式为:

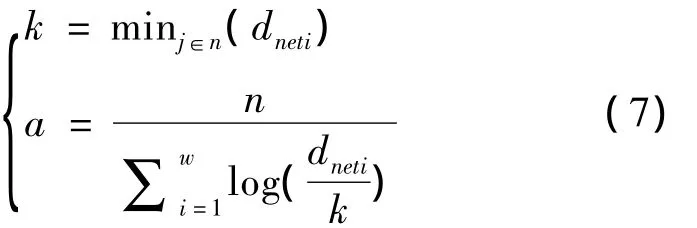
其中dneti为第i个包的网络传输延时。此时即可估算出由抖动缓冲引起的丢包率Pplbuff:

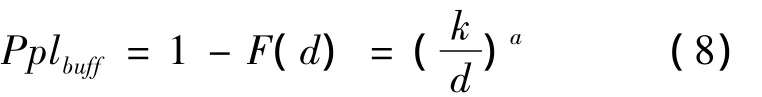
在一次长度为60S的VoIP通信过程中，我们测得缓冲区丢包率的帕累托分布建模预测值与真实值之间的误差如图2所示:

通过图2可以看到，除通信开始时误差较大以外，随着通信的进行，预测值与真实值的误差大多保持在1%以下。由此可以得到，帕累托分布对抖动

缓冲丢包率的预测是非常准确的。

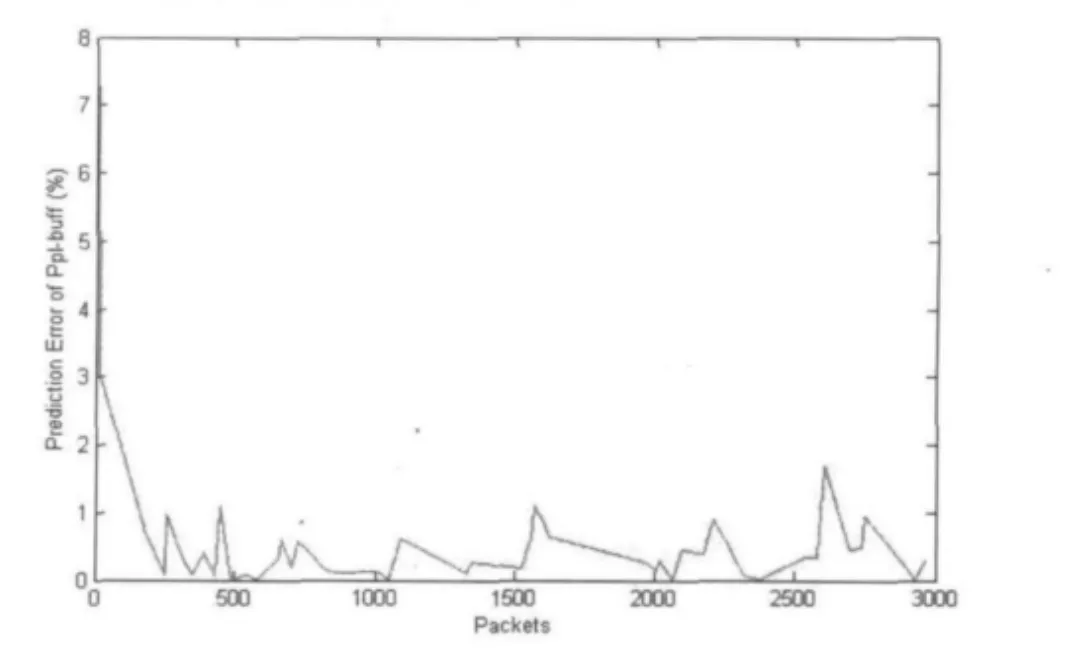
图2 Pplbuff的预测值与真实值误差分析

2.3MAX-MOS算法

将公式(7)(8)带入公式(2):

通过公式(9)可清楚的看出:在网络条件一定，也就是说抖动jitter、网络延时dnet一定，网络丢包Pplnet一定的情况下，Id的值将会随着缓冲区尺寸dbuff增大而增大;Ie的值会随着dbuff增大而减小，R值只与缓冲区大小dbuff有关，此时，MOS值也只与缓冲区大小dbuff有关可以表示为:MOS=fMOS(dbuff)。

研究表明，在网络单向延时d小于400ms，延时处于可以忍受的程度;当大于400ms，会导致丢包和乱序，严重影响语言的重现，MOS值也降到了3以下，达到“几乎所有用户不满意”的级别，难以保证正常通信［9］;丢包率在8%-10%以下语音质量尚可容忍［3］。在这两个条件的约束下，对公式(9)进行简化、分析可以得到如下结论:网络条件一定的情况下，MOS值随dbuff变化呈现的是一个凸函数，且该函数的极值点一定出现在dbuff［0，400］这个区间内。

在开放源代码OPENsip［10］中，通过统计可以得到，当网络丢包率5%，jitter方差为654.80，平均网络延时30.2ms，突发比1.06，传输10S的音频，采用G.711编码，平均MOS值和缓冲区尺寸dbuff之间的关系，如图3所示:

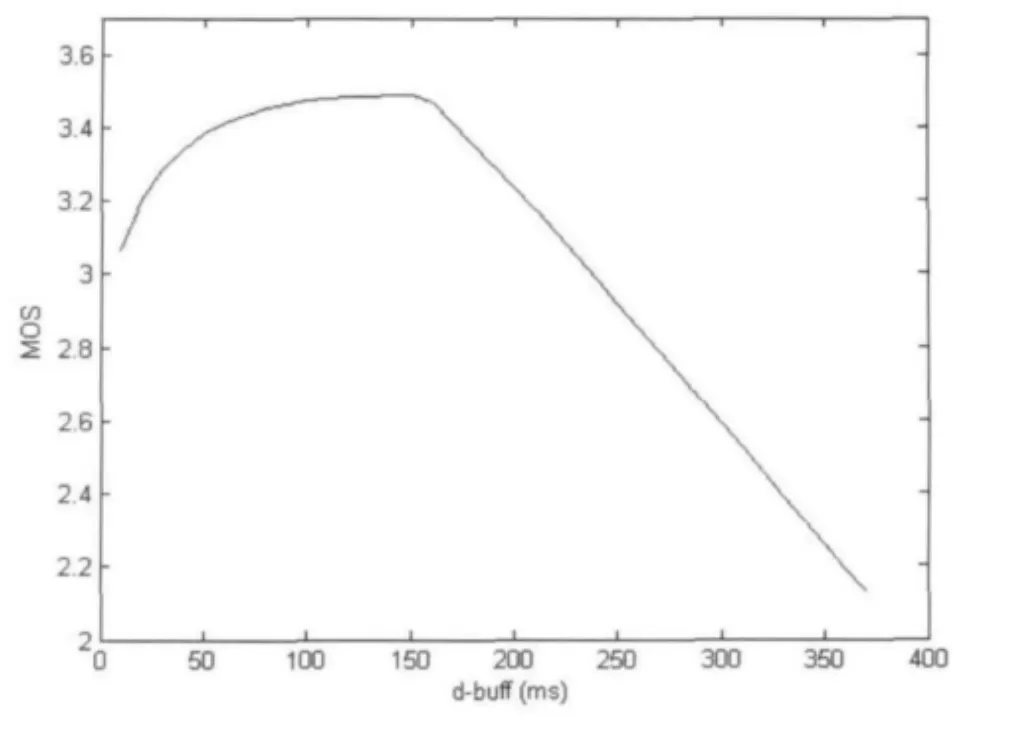
图3 网络条件一定情况下MOS值与缓冲区尺寸dbuff之间的关系

通过以上分析以及图3的统计数据可以得到这样的结论:在网络条件一定且满足VoIP通信最低要求的情况下，一定存在某一缓冲区尺寸使得因抖动缓冲引起的丢包和因缓冲区引入的延时达到一个平衡，这个平衡点处的MOS期望值最大。

我们提出了如下的自适应抖动缓冲算法:

定义调整周期:上一次设置缓冲区时刻到下一次设置缓冲区时刻之间的时间长度。

(1)在当前调整周期结尾处，采用E-Model方法计算当前调整周期内的平均MOS值，此MOS值为该周期内真实MOS平均值;

(2)根据当前调整周期内数据包的历史延时数据，求出网络延时平均值 dnet、网络丢包平均值Pplnet，更新帕累托分布参数k、a，并估算抖动缓冲所引入的丢包率Pplbuff;

(3)利用反复计算取最大值的方式，将当前网络状况下所允许的所有缓冲区尺寸带入公式(9)，求其最大MOS期望值，并取出MOS期望最大值时的缓冲区尺寸;

(4)为下一调整周期设置最优缓冲区尺寸;

(5)返回(1)。

简要算法流程如图4所示:

在算法的第一步，我们测量的是上一调整周期内真实的MOS平均值;在第三步中，我们搜索下一调整周期最优缓冲区尺寸，并估算最优缓冲区尺寸下的期望MOS值。利用2.3节中的网络环境，我们测量了一段时间内真实MOS值与估算的期望MOS值之间的关系如图5所示:

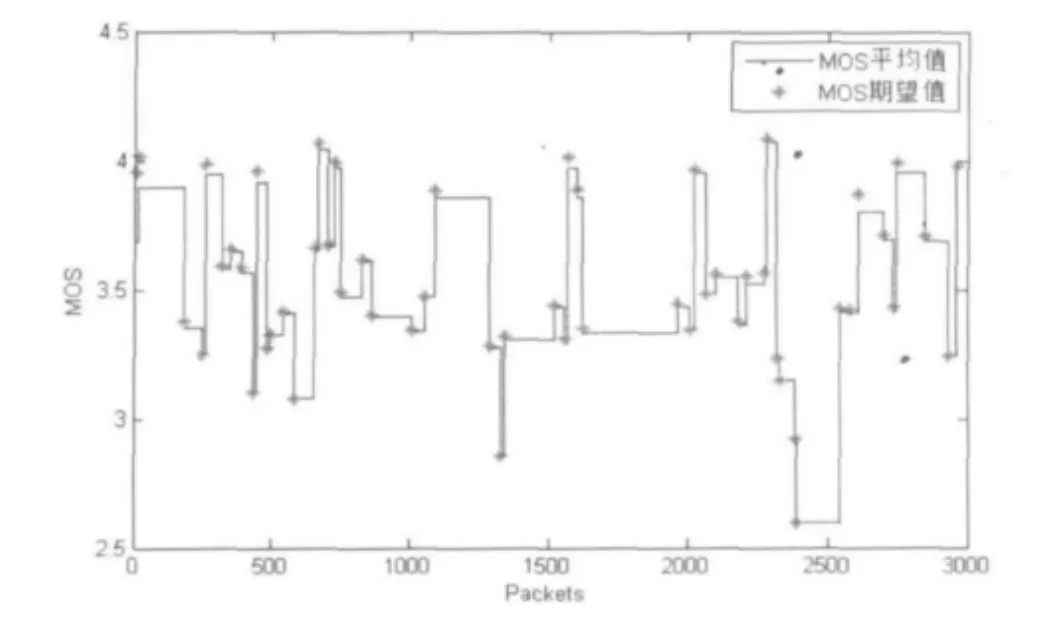
图5 真实MOS值与期望MOS值之间的关系

由图5可以清晰的看到期望MOS值能够非常好的预测下一调整周期内的平均MOS值，绝大多数误差在百分之一以下，平均误差0.35%，准确度令人满意。

2.4 关键问题论述

以上流程中，有两个关键问题:一是用于延时分布的调整周期数据窗设置问题;二是最大MOS搜索问题。对于第一个问题，数据窗的大小设置要在准确性和灵敏性之间取得平衡，设置过大虽准确性有所提升，但牺牲的是算法的灵敏性;设置过小则不能准确的反映当前的网络状况，也就无法对Pplbuff进行有效预测。我们对比了大量类似的自适应抖动缓冲研究领域的文献［1］［4］［5］，这些文章大多考虑到了这个问题，但很少提出解决方法，只是按照自己的经验设置了一个固定大小的数据窗。这样做对于某些特定的网络状况可能很有效，能够得到非常理想的测量数据，运算过程也会相对简单;但缺乏灵活性，当网络状况发生非常频繁、剧烈的波动时候，数据窗设置的大小就会很大程度上影响算法的准确性。我们在实验过程中利用的是开放源代码OPENsip来测试我们的算法，SIP内部在接收端也做了自适应的抖动缓冲区。我们发现，SIP内部在调整抖动缓冲区的时候并不是采取固定数据窗大小的模式，而是利用内部一整套判别网络状况的机制根据当前网络状况变化自适应的判定是否进行buffer控制。经过多次实验证明，这个网络状况判定机制是稳定、准确的。本文算法中利用到了这个机制，在网络状况发生改变的时候，对buffer进行设置，这就相当于根据网络状况自适应的调整了数据窗大小。

对于第二个问题，通过以上论述得到MOS值只与dbuff有关，可以表示为MOS=fMOS(dbuff)。直接求函数极值存在两个问题:一是函数式包含了多个复杂计算在内，很难确定;二是做该函数的极值计算具有较高的复杂度，编程语言很难实现。故最优缓冲区尺寸的查找不宜通过直接求极值方式求得。针对这个问题，我们提出了一种简单的反复计算求最大值法:在不考虑d＞400ms的情况下，将dbuff的所有可能取值依次带入公式(9)计算MOS期望值，并取其最大值，这样就可以在有限的次数内查找到最优缓冲区尺寸。

3 仿真实验与结果

本文采用了开放源代码PJSIP作为算法实验的平台［10］。通过加入本文提出的自适应抖动缓冲算法代替原有的的抖动缓冲算法，在原项目已有的抖动缓冲仿真项目中对话音传输的整个过程进行了仿真。

文献［11］在两状态马尔科夫模型，也就是吉尔伯特模型基础上建立了网络丢包仿真系统，可以很好的模拟出实际的网络丢包状况。故本文采用吉尔伯特模型为网络丢包进行计算机建模。吉尔伯特模型可以表示为图6所示:

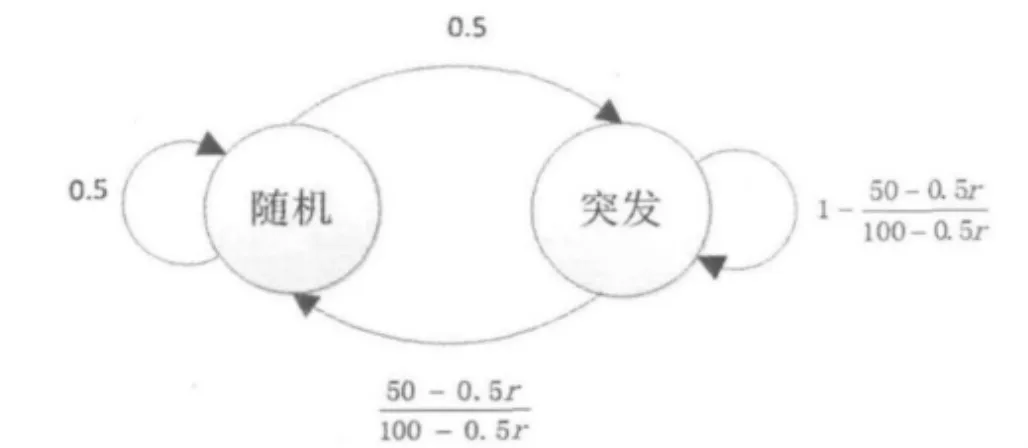
图6 网络丢包吉尔伯特模型

其中参数r为仿真系统内部定义的突发关联系数，取值范围为0～100。r与突发比BurstR的关系为:

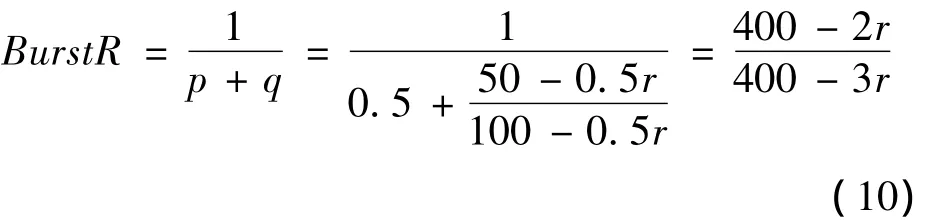
仿真实验采用G.711语言编码，在多种网络条件下对SIP原有自适应抖动缓冲算法和本文提出的MAX-MOS算法分别进行了测试。设定最小及最大突发丢包数分别为0和20，每次仿真时间为1分钟，且均在某一网络状况下进行多次测量以取平均值。仿真结果如下图7所示:

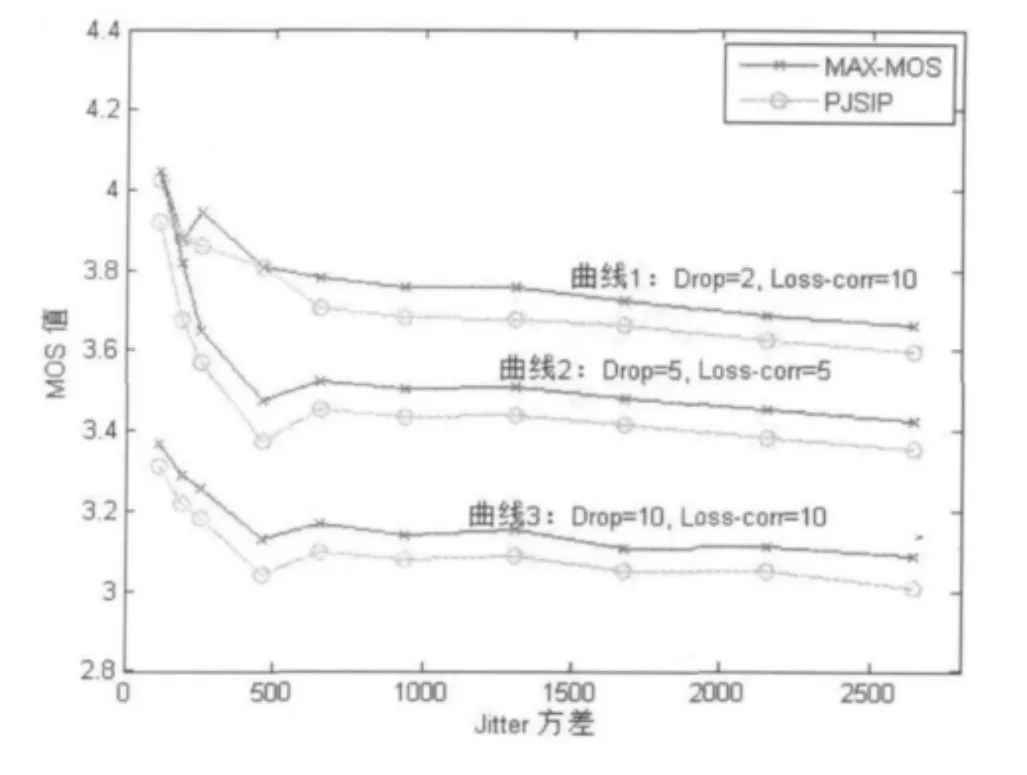
图7 仿真测量结果

三组曲线的网络丢包率分别设定为2%、5%、10%，丢包关联系数分别设定为10、5、10。通过图7我们可以看到，随着jitter方差的增大，MOS值在逐步下降;在绝大多数网络状况下本文提出的MAXMOS算法得到的MOS值均比SIP原有自适应抖动缓冲算法得到的MOS值要大。

4 结论

本文从提高VoIP服务质量出发，提出了一种基于E-Model的MAX-MOS自适应抖动缓冲算法。该算法采用帕累托分布为单向延时分布进行建模，估算接收端抖动缓冲丢包率;利用最新的E-Model算法计算当前语音质量;通过反复计算取最大值的方法查找延时与丢包率之间的平衡点，最终自适应的设置接收端的缓冲区大小。本文在实验阶段采用开放源代码OPENsip作为本文算法的实验平台，很好地利用了其中自适应设置数据窗的机制，还利用了SIP工程中的抖动缓冲仿真项目。实验结果表明，本文算法在大多数网络状况下得到了服务质量要优于SIP原有算法，可以有效的提高服务质量。

［1］李敏.VoIP系统中语音质量的研究与测试［D］.武汉:华东科技大学，2008.

［2］S Paulsen，K Nowicki.Influence of the Jitter Buffer on the Quality of Service VoIP［C］.Third International on Ultra Modern Telecommunications and Control Systems，2011.

［3］R Ramjee，J Kurose，D Towsley，H Schulzrinne.A-daptive Playout Mechanisms for Packetized Audio Applications in Wide-Area Networks［J］.IEEE，Toronto，Canada.

［4］Huang S F，Chang P C，Wu E H.Adaptive voice smoothing with optimal E-Model method for VoIP services［J］.IEICE Transactions on Communication，2006，E89-B(6):1862-1868.

［5］蔡铁，龙志军，伍星.基于语音质量预测的VoIP自适应抖动缓冲算法［J］.计算机工程与应用，2011，47(10):63-66.

［6］ITU-T Recommendation G.107 The E-model:a computational model for use in transmission planning［S］.12，2011.

［7］ITU-T Recommendation G.113 Transmission impairments due to speech processing［S］.11，2007.

［8］Wei Zhang，Jingsha He.Modeling End-to-End Delay Using Pareto Distribution［C］.Proceedings of IEEE Second International Conference on Internet and Protection，2007.

［9］ITU-T Recommendation G.114 One-way Transmission time［S］.2003.

［10］开放源代码 OPENsip官网［OL］.http://www.pjsip.org，2013.

［11］兰帆，张尧弼.基于Gilbert模型的网络丢包仿真［J］. 计算机工程，2004，30:200-201.

［12］K Fujimoto，S Ata，M Murata.Adaptive Playout Buffer Algorithm for Enhancing Perceived Quality of Streaming Applications［J］.IEEE Globecom，2002.

Research of An MAX-MOX Adaptive Jitter Buffer Algorithm

LAI Zhen-yu，WANG Xuan
(ECDAV，Communication University of China，Beijing 100024)

Jitter is an important factor affecting the quality of VoIP services.VoIP systems usually reduce the effects of jitter by setting the jitter buffer as much as possible.This paper achieves one-way delay model which is based on the Pareto distribution.Then the E -Model method is used to calculate the MOS values.Finally，the buffer size is set by searching for a good compromise between latency and packet loss ratio.Having considered all those ways above，the MOS values promotion is acquired adaptively.Experiments show that the algorithm effectively improve the quality of VoIP system services in a variety of network conditions.

VoIP;E-Model;MOS;adaptive jitter buffer

TN364

A

1673-4793(2013)03-0063-06

2013-03-19

来振宇(1987-)，男(汉族)，河北廊坊人，中国传媒大学硕士研究生.E-mail:laizhenyu@cuc.edu.cn

book=0,ebook=424

(责任编辑

:宋金宝)