城市隧道口交通优化方案研究

徐晓丹，林 丽

(南京林业大学汽车与交通工程学院，南京210037)

城市隧道使城市道路交通形成立体交通模式，消除了城市道路交叉口车流、人流的相互影响，减少了地面车流的干扰，使交通流能够快速地通过路段，减少了道路的占用时间。我国的相关设计规范［1］规定了隧道出口与平面交叉口的距离要满足具体的设计要求，但是由于城市地下道路构造上的特点，决定了其交通受限于出入口，几乎所有的城市隧道都不同程度地存在着出入口交通瓶颈问题［2］。严重时造成城市隧道及其周边道路交通阻塞，影响了道路的通行能力。目前，城市隧道出口的对外衔接组织形式有多种，本文选用的“隧道+地面”形式主要是车辆驶出城市隧道出口后在较短距离内，立即进入信号交叉口区域的这样一种情况，具体组织形式如图1所示。在此基础上，分析观测数据与通行能力计算结果，形成城市隧道出口衔接路段长度模型，并结合实例仿真验证。隧道出口衔接路段的合理设置，有利于提高衔接路段的通行能力，便于交通组织和交通管理，同时对于提高行车安全也具有重要意义。

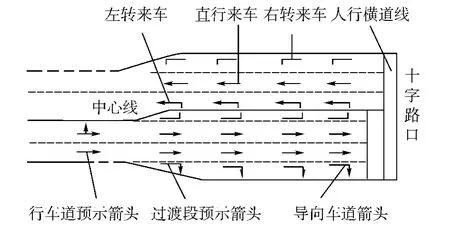
图1 出入口与十字型路口衔接［3］Fig.1 The entrance and exit link up with intersection

1 城市隧道出口安全距离的确定

1.1 城市隧道出口安全距离的影响因素

将隧道出口段满足车辆安全行驶所需的距离定义为隧道出口安全距离 (简称L安)。影响安全距离的因素有很多，但是根据研究表明，驾驶员在驾驶过程中接收的所有信息中，凭借瞳孔所获取的占80%～90%，所以驾驶员的瞳孔是获取外界信息的主要方式，由于驾驶员受到隧道进出口明暗适应的影响，其驾驶行为存在一定的危险性;另外，隧道出口线形直接会使车辆产生加速或减速。

(1)驾驶人视觉适应能力分析。首先定义驾驶人光适应过程中的瞬时盲期现象为视觉震荡。通过瞳孔面积最大瞬态速度值 (MTPA)指标，将瞳孔面积变化速度及换算视觉震荡持续时间结合，能合理解释隧道进出口路段视觉负荷。

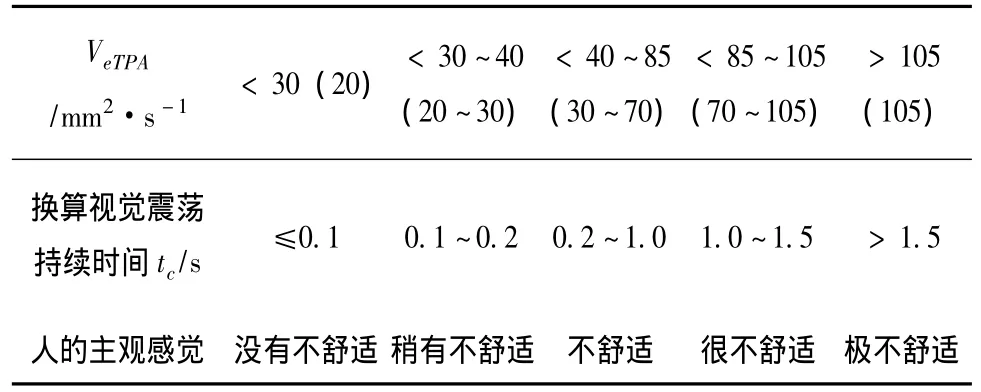
表1 VeTPA与视觉舒适度关系［4］Tab.1 Relationship between VeTPAand visual comfort degree of tunnel entrance and exit

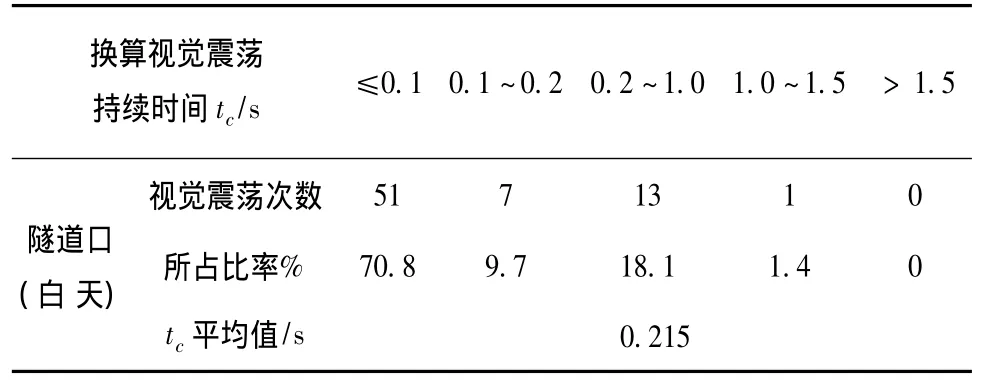
表2 隧道进出口行车试验换算视觉震荡持续时间Tab.2 Conversion duration for visual turbulence of tunnel entrance and exit by driving experiment

综合考虑城市隧道的限制条件，结合道路通行能力及车速限制等城市道路环境的安全因素，主要考虑了城市隧道出口视觉震荡对行车安全的影响。由表1、表2可知，当换算视觉震荡持续时间大于1.5 s时，驾驶员的主观感觉为极不舒适;城市隧道出口的一般限速V为40～60 km/h，根据L安=V×tc，当tc取1.5 s时，算出的隧道出口安全距离为17～25 m，所以为了保证安全，取换算视觉震荡持续时间tc为2 s，得到隧道出口安全距离公式L安=2V，V为隧道出口的设计车速(规定的最大行驶车速，暂不考虑线形产生的加速度)。

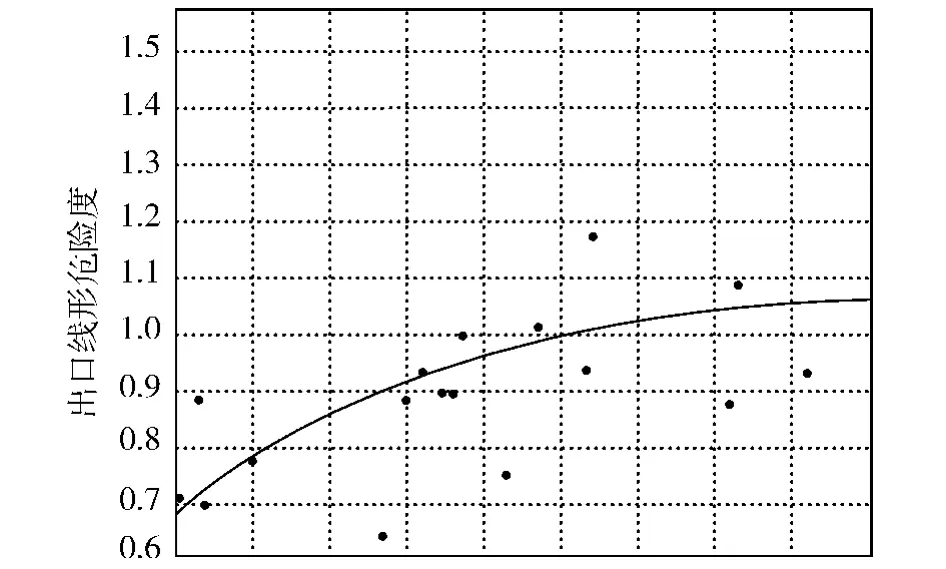
图2 出口加速度与线形危险度关系［7］Fig.2 Relationship between the export acceleration and the alignment risk degree

(2)道路线形的影响分析。在不同的道路交通环境下，道路线形对车辆的行驶速度有较大影响，且不同的线形指标对车速的影响程度也不一样。为综合反映道路线形与车速变化的关系，引入线形危险度的概念［5］。隧道出口加速度与线形危险度的关系如图2所示。

可能受到道路条件和照明条件的影响，加速度与线形危险度有一定的离散性，但是仍可以得出结论:出口线形危险度越大(线形越差)，其加速度值越大，即车速变化越大，行车越不安全。当车辆驶出隧道时，驾驶人会根据前方线形采取驾驶操作，当线形较好时会采用较大的加速行为，当线形差时会采用较小的加速行为，甚至会减速，这时隧道出口外与隧道出口处存在车速差［6］。

1.2 隧道出口车速的变化

驾驶人心理行为、几何线形和道路环境等多方面要素最终都以车辆运行速度的形式反映出来。因此，本文将车速作为建立隧道出口道路线形、驾驶人视觉影响和道路交通安全的“桥梁”。当车速有较大落差时，往往会使驾驶人措手不及，导致行车事故，而这种速度的不连续一般是由于线形突变所致。车速的变化影响安全距离的变化，道路线形和驾驶员的视觉震荡现象都是以车速变化的方式体现，本文在建立隧道出口安全距离模型中，将车速作为重要参量。

1.3 安全距离分析与确定

受到视觉震荡的影响，假设驾驶员在这段时间内不采取任何驾驶操作，则车辆在隧道出口的坡道上减速，其加速度值与隧道坡度i有关，即得隧道出口安全长度L安公式:

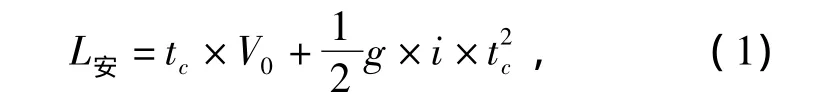
式中:tc为视觉震荡持续时间，取2 s;V0为车辆刚出隧道时的初速度 (取隧道出口设计车速)，m/s;g为重力加速度，取9.8 m/s2;i为计算范围内的平均坡度。

城市隧道出口与相邻交叉口之间的衔接段长度比高速公路隧道出口衔接段长度短很多，城市隧道出口的最大纵坡不超过6%［8］，在视觉震荡期间，根据公式 (1)中的第二项，可知0.5×9.8×6%×22=1.176 m，值较小，出口纵坡对车速的影响程度可以考虑不计，因此公式1可调整为:

在公式 (2)中，2 s为视觉震荡持续时间(tc)。由此，可以明显看出，影响隧道出口安全距离的因素最终用车辆行驶速度来体现。

2 交叉口排队长度的确定

信号交叉口制约了城市主干路的通行能力，由于信号交叉口的通行能力低于路段通行能力，交通量稍微过大就会诱发交通拥挤，导致车辆在交叉口排队。信号交叉口的排队长度，能反映交叉口车流的运行情况，它对评价交叉口的运行效率、现状信号配时方案的优劣等都有重要意义。

2.1 排队长度模型选取

本文选定SIGNAL94的优化模型［9－12］作为基本框架，该模型只有离散系数需要标定，模型精度高，且利用现有观测的数据可以很好地对模型参数进行修正。通过分析其在实际交通流变化情况下的实用性，建立符合信号交叉口交通流特性的排队长度优化模型。

图3 各信号灯周期排队车辆数Fig.3 Length of queues in the each signal cycle

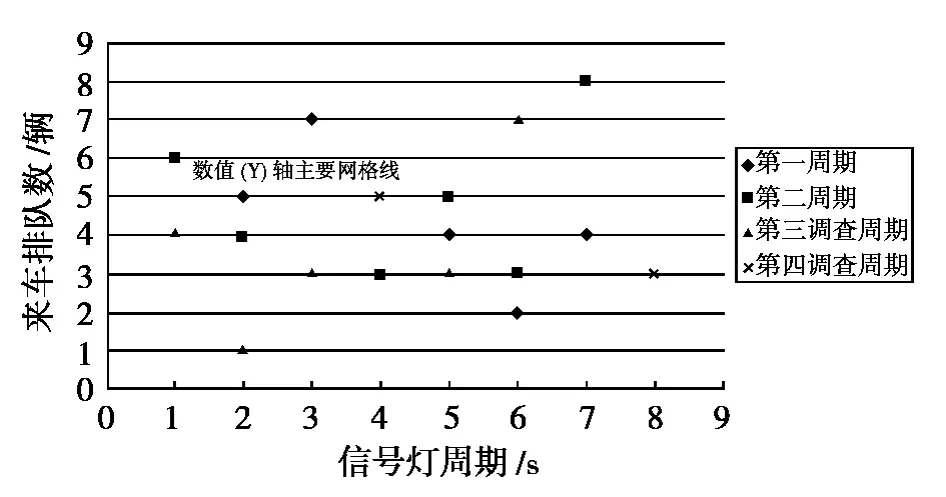
图4 来车排队分布散点图Fig.4 Scatter diagram of queuing vehicles

模型中最关键的是确定路口饱和流率和确定车辆到达率。饱和流率是指当交叉口有相当长的车辆排队等待时，有效绿灯时间内通过的最大小时车辆流率。车辆到达率是指单位时间内到达交叉口的车辆数。经优化后的SIGNAL94公式模型:

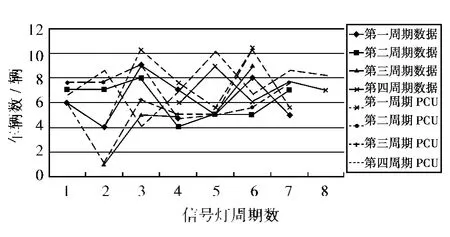
图5 各信号灯周期放行车辆数Fig.5 Vehicles in green light period

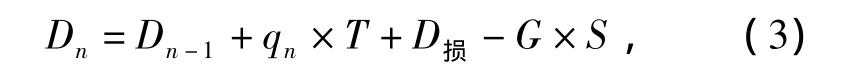
式中:Dn为第n周期的最大排队长度，辆;Dn－1为第n－1周期滞留下来的车辆数，辆(无二次排队，Dn－1=0);qn为第n周期的车辆到达流率，辆/s;T为信号灯周期的长度，s;G为绿灯时长，s;S为饱和流率，辆/s;D损为启动损失时间通过的车辆数，辆。

其中，T、G是通过实际观测;D损是通过数据后，绘制散点图如图3所示;qn、S是通过实测后扩样得到如图4和图5所示。对调查数据进行处理后得出，在交叉口有效绿灯时间里，根据连续5 s以上车流通过的车辆到达数，可以计算出饱和流率与车辆到达率。得到车辆到达率的统计分布如图6所示。

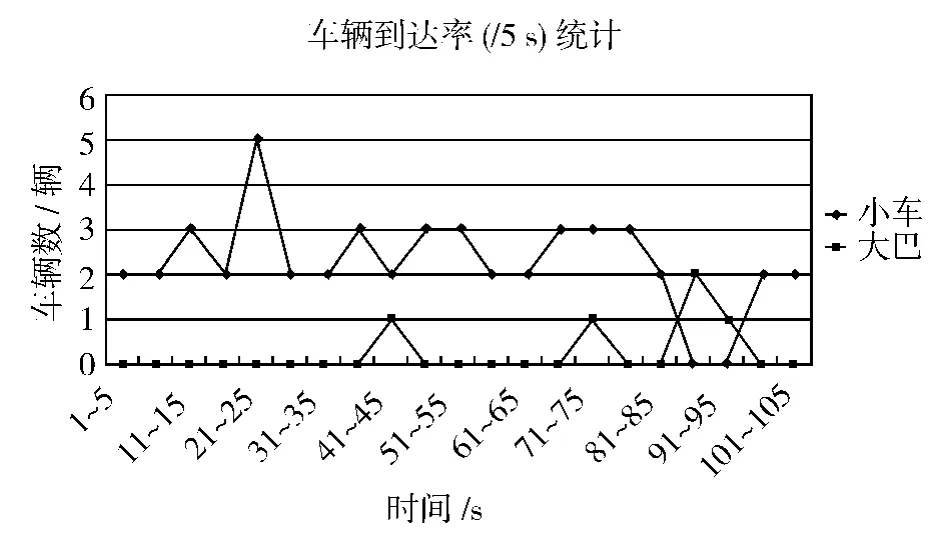
图6 车辆到达率统计Fig.6 Statistical graph of approach flow rate

2.2 交叉口排队长度的确定

由于排队长度L排队=Dn×L间(车头间距)，Dn根据公式 (3)得出，由此，交叉口排队长度公式为:

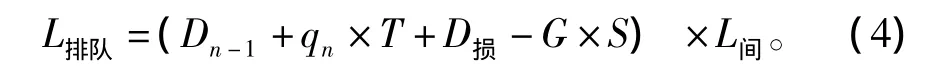
在本次研究中，车辆能在交叉口功能区顺畅通行的评判标准为不发生二次排队。根据对采集的玄武湖隧道出口车辆到达率、交叉口信号配时等相关数据的分析，建立了交叉口排队长度模型。

3 隧道出口衔接段长度模型确定

3.1 城市隧道出口衔接段长度定义

城市隧道出口衔接段长度由隧道出口安全距离和交叉口通行能力两者共同影响确定，因此定义城市隧道出口(洞口开始)与交叉口停车线之间的这段距离为城市隧道出口衔接段长度，简称L衔接。

3.2 衔接段长度模型建立

通过前两部分的研究，发现对城市隧道出口安全距离及交叉口排队长度起主要影响作用的是车速和车辆到达率两个因素，综合考虑，优化整合成如下模型:式中:a为调节交叉口车辆到达率对模型的影响程度;b为调节隧道出口车辆速度对模型的影响程度。

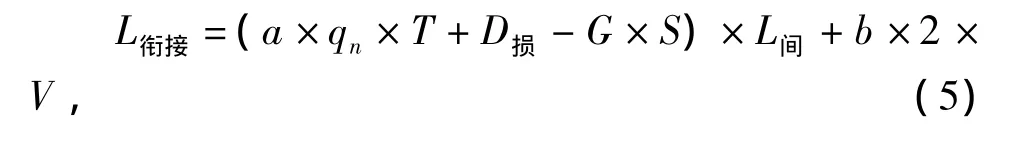
通过MATLAB对数据进行处理，可以分析得出系数a与b之间关系图像如图7所示。

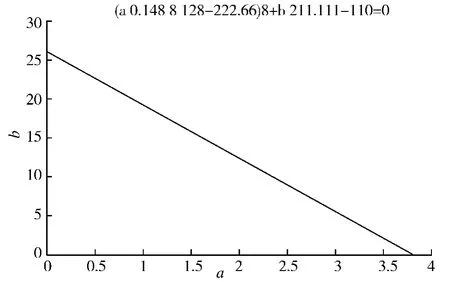
图7 衔接长度符合要求时的a、b关系图Fig.7 Relation graph of a and b when the connected-link meet the requirement

根据玄武湖隧道出口衔接的中央路—新模范马路交叉口实测数据，实际分别计算的两段长度L安与L排队之和是小于100 m的。根据分析结果，L衔接为100 m、110 m、120 m时，a、b线性相关且斜率相等，即:

在交叉路口流率、信号灯配时与隧道设计速度一定时，b≥1时，a＞1(如图7所示)，这时长度满足所研究的通畅与安全的要求，无需改进;当b＜1，a≥1时，说明隧道出口安全距离实际值小于理论值，则要适当降低隧道设计车速以保证行车安全;当b≥1，a＜1时，说明交叉口排队长度不满足理论要求，则要对信号灯进行配时优化。

综上所述，隧道出口处距交叉口停车线的实际长度L实际小于理论值L理论时 (L实际＜L理论)，根据公式 (5)对信号灯配时以及隧道设计车速进行调整，使其满足要求。

4 验证可靠度

4.1 建立仿真

针对提出的长度计算模型，借助VISSIM进行交叉口交通流仿真。具体以鼓楼隧道出口为例，该隧道出口与玄武湖隧道出口的组织形式相似，在很短距离内直接与中央路－傅厚岗交叉口衔接，工作日高峰时期经常出现严重的排队现象。以隧道出口实测的现状交通量数据为基础，建立仿真模型，得到现状仿真效果如图8所示。

图8 隧道出口衔接相邻交叉口Fig.8 Situation of the exit of urban connecting the nearest intersection

4.2 检测数据输出

现状排队长度与改善后排长度检测数据见表3和表4。

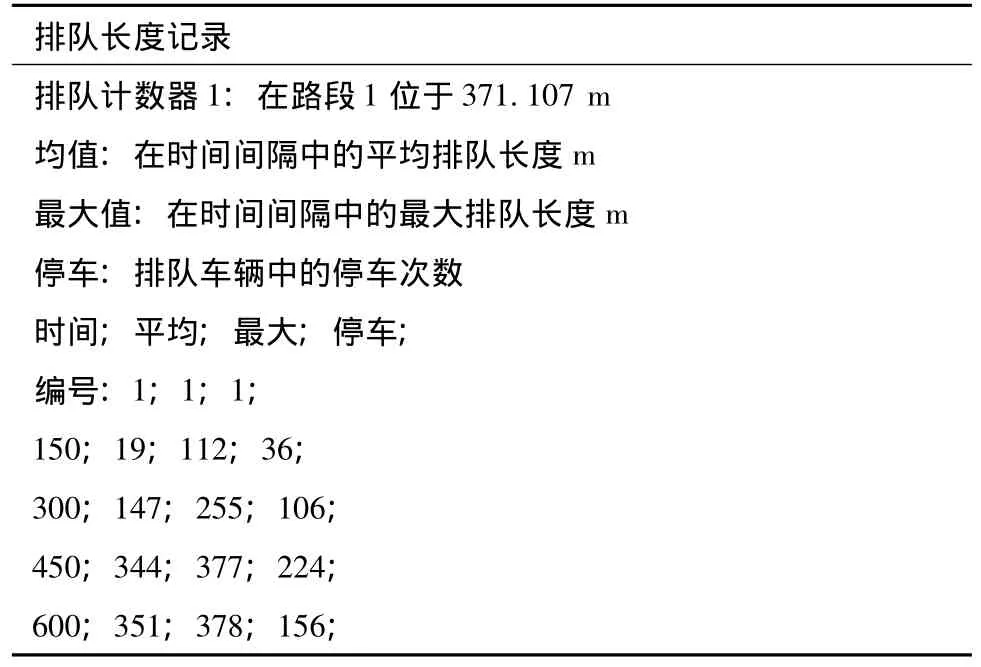
表3 现状排队长度检测数据输出表Tab.3 Output of the detected queues at present

4.3 仿真结果分析

VISSIM的排队计数器可以提供三类数据:平均排队长度;最大排队长度;排队车辆的停车次数。这里所指的排队是从上游路段或连接器的排队计数器的设置位置开始计数，直至排队状态下的最后一辆车。从图8可以看出，在现状交通管理条件和道路条件下，高峰时段鼓楼隧道出口(南进口)交叉口出现了严重的排队现象，已经排到隧道里面，故该段隧道出口衔接段长度设置有待完善。通过改善优化后，重新建立仿真，得到仿真效果如图9所示，在该衔接段长度上，排队长度已经减小。由输出数据表3和表4中也可以看出两种情况的排队长度是有差别的，故证明该衔接段长度模型有可行性。

4.4 具体改善措施

为了尽量减少工程量，对现状的衔接段长度不做大的改动，根据鼓楼隧道出口与其相邻交叉口的实例仿真，利用建立的衔接段长度模型，可以提出相应的交通管理改善方案。为减少隧道出口车辆的排队长度，同时采取以下3种措施。

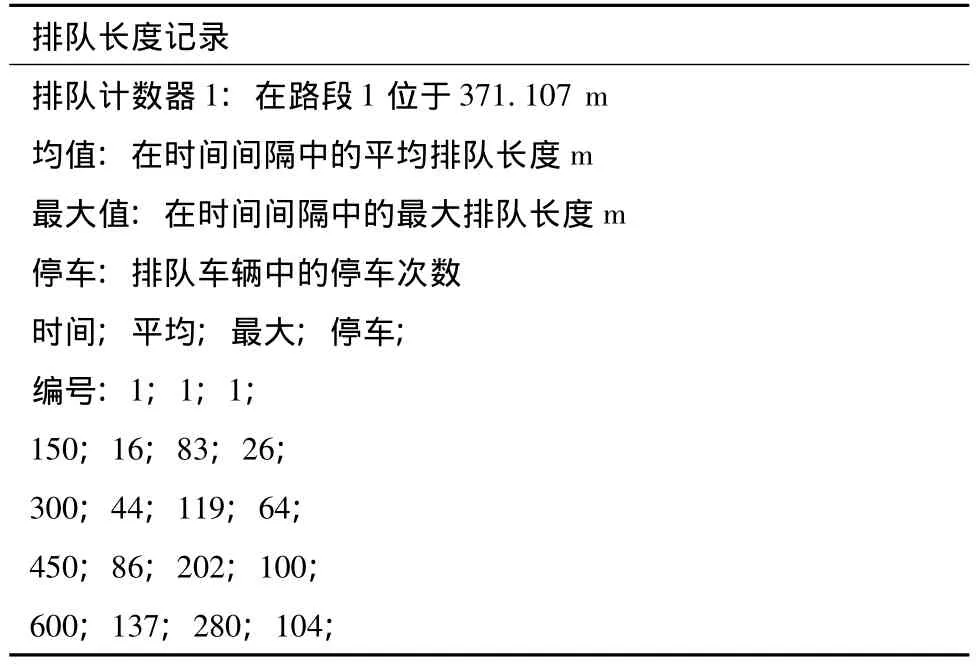
表4 改善后排队长度检测数据输出表Tab.4 Output of the detected queues after improvement

(1)调整中央路—傅厚岗交叉口信号配时，尽量增加南北向直行的绿灯时长，提高中央路的通畅性，减少车辆排队长度。

(2)拓宽傅厚岗东侧一个出口车道，保证东西向不发生延误。

(3)适当降低隧道的设计车速，从而减少隧道出口车辆的排队长度。

5 结束语

本文从城市隧道出口交通流特性出发，根据驾驶人视觉适应能力、隧道出口道路线形及车速等因素的分析，确定隧道出口的安全距离;并通过对相邻交叉口的排队延误分析，提出了适应此类交通流特性的排队优化模型。该模型分别考虑了隧道出口和交叉口两个方面的不同因素，在已建城市隧道出口实际衔接长度不满足理论值的情况下，为减少对衔接路段的施工，可通过现状交通流相关数据带入长度模型，改变交叉口信号配时、限制隧道出口车速等相关交通管理措施，来缓解交通拥挤，提高行车效率与安全性，同时该长度模型对新建隧道出口衔接路段设计有重要参考价值。以上研究是根据玄武湖隧道出口的数据而进行的分析，具有一定的特殊性，随着研究和实践的深入，模型将会得到进一步的完善。

［1］DGJ08－96，城市道路平面交叉口规划与设计规程［S］.

［2］刘 韵.城市地下快速道路建设动因分析［J］.地下空间与工程学报(增刊)，2006，2(8):1293 －1296.

［3］李素艳，杨东援，赵娅丽.地下道路出入口交通组织研究［J］.地下空间与工程学报，2007，3(4):781 －786.

［4］杜志刚，潘晓东，杨 轸，等.高速公路隧道进出口视觉震荡与行车安全研究［J］.中国公路学报，2007，20(5):101 －105.

［5］郭忠印.公路隧道进出口运行安全研究——中期报告［R］.上海:同济大学，2005.

［6］郭忠印，孔令旗.隧道进出口运行安全研究［R］.上海:同济大学，2008.

［7］杨 轸，郭忠印.隧道进出口车速变化研究［J］.上海公路，2006，1:48 －51.

［8］DG/TJ08－2033－2008，道路隧道设计规范［S］.

［9］隽志才，魏丽英，李 江.信号交叉口排队长度宏观模拟的自适应分析法［J］.中国公路学报，2000，13(1):77 －80.

［10］周学农.排队长度模型比较及动态方法研究［J］.交通运输系统工程与信息，2006，6(1):91 －95.

［11］颜桃为，马健霄，马 亮.信号交叉口安全评价体系研究［J］.森林工程，2010，26(1):49 －52.

［12］荣 建，何 民，陈春妹.信号交叉口排队长度动态计算方法研究［J］.中国公路学报，2002，15(3):101 －104