基于灰色系统和神经网络的钟差预报

雷雨，赵丹宁，高玉平



基于灰色系统和神经网络的钟差预报

雷雨1,2,3，赵丹宁1,3,4，高玉平1,2

（1. 中国科学院国家授时中心，西安 710600；2. 中国科学院时间频率基准重点实验室，西安 710600； 3. 中国科学院大学，北京 100039；4. 中国科学院精密导航定位与定时技术重点实验室，西安 710600）

灰色系统；神经网络；钟差预报

0 引言

钟差预报在导航定位、守时和GPS不完整星座定位和接收机自主完好性监测（receiver autonomous integrity monitoring，RAIM）等方面具有非常广泛的用途。在卫星导航定位中，导航电文实时发播卫星钟改正数，以满足实时导航定位的需要[1]；在守时实验室中，控制守时参数，以输出高精度的时间同步信号[2-3]；在不完整星座（卫星数小于4颗）条件下，接收机钟差可作为一颗可视卫星辅助定位[4-5]；在RAIM中，接收机钟差可作为一个辅助量参与故障卫星的检测与识别[6-7]。较常用的钟差预报模型为多项式模型，该模型计算简单、参数易估计，但很难用于复杂时间序列的处理。无论是星载钟、地面原子钟还是普通晶体振荡器，都是非常敏感的，极易受到外界环境及自身因素的影响，很难掌握其复杂细致的变化规律，因此可将钟差的变化过程视为灰色系统。GM（1，1）模型是灰色系统中最常用的钟差预报模型，许多学者对其进行了研究，并取得了显著的效果[8-9]。GM（1，1）模型可以基于较少的历史数据建立预报模型，与一般的外推预报不同点在于它不用原始数据建模，而用一阶累加生成模块建模，一定程度上弱化了数据的随机噪声，从而更好地反映有用信息。

GM（1，1）模型在预报中，对历史数据作不同的取舍时，因其所建模型不同，钟差预报值也不相同，即这种预报结果将是一个预报值的区间，究竟哪个值是最准确的？应该采用何种模型预报？为了减少模型选择的盲目性，一种可行的办法是将不同的预报模型结合起来。鉴于此，本文将GM模型与神经网络（neural network，NN）结合起来，提出了基于灰色系统与神经网络的钟差预报模型。

1 基本思想

为了克服上述困难，一种可行的办法是将不同的预报模型结合起来。较简单、常规的方法是加权线性组合方法。这种组合方法是单一方法的凸组合，并且要求参加预报的GM（1，1）模型的误差能保持稳定，但钟差预报误差往往是非均匀性的，因而此方法就存在不足[10]。为此，有必要考虑用非线性的方法来组合单一方法的结果，而神经网络是解决非线性问题的有效工具[11]。

神经网络能够通过训练学习以任意精度逼近任意函数，特别适用于非线性系统的预报[12]。神经网络模型对样本数据的依赖性强，要求训练样本能较好地覆盖系统的变化特征。而GM（1，1）模型能够提取钟差变化的趋势项，一定程度上滤去或减弱噪音或干扰，从而更加客观地反映有用信息，因此将GM（1，1）模型的预报值及对应的实际值作为网络的样本能更好地反映钟差序列内部规律，增强网络的映射能力。

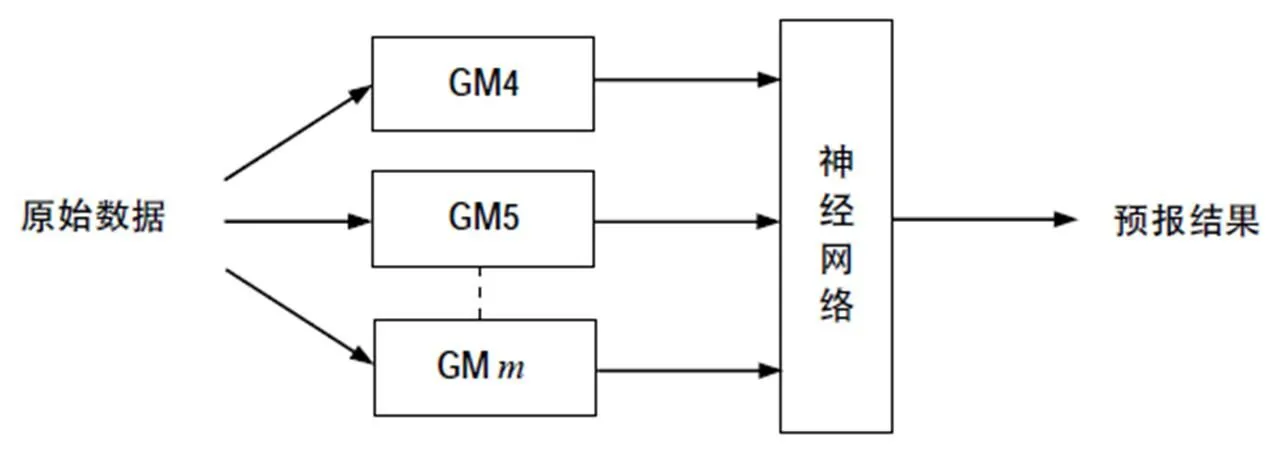
图1 基于灰色系统和神经网络的钟差预报模型

该模型可理解成灰色系统与神经网络的“串联”，实质上是将不同GM模型作为网络的输入，借助神经网络强大的非线性映射能力，对其进行非线性组合，得到一个组合预报值。文献[9]采用了此模型对电力系统负荷进行预测。

2 具体实现

2.1 钟差序列灰色建模

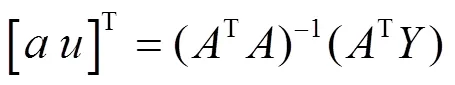
式（3）中，

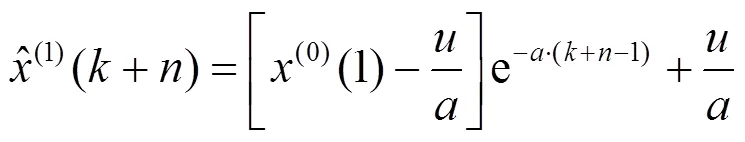
需要说明的是，在建模前，必须保证原始序列中各项符号一致，若不一致，则给每个元素都加上1个常数，使序列的符号一致，然后在此基础上建立GM（1，1）模型并进行预报，最后再从预报值中减去所加常数即为最终值。常数的取值原则是，该常数的符号与原始序列中绝对值最大的数的符号一致，且其绝对值要大于原始序列中绝对值最大数的绝对值。

2.2 基于神经网络的非线性组合

常用的神经网络算法有反向传播（back propagation，BP）神经网络、径向基函数（radial basis function，RBF）神经网络和广义回归神经网络（generalized regression neural network，GRNN）。GRNN是一种新型的神经网络，建立在核回归数理统计的基础上，能够根据样本数据逼近其中隐含的映射关系[13]。即使样本数据稀少，网络的输出结果也能够收敛于最优回归表面[14]。其数学模型为[14]

选用多元的高斯分布作为核函数：

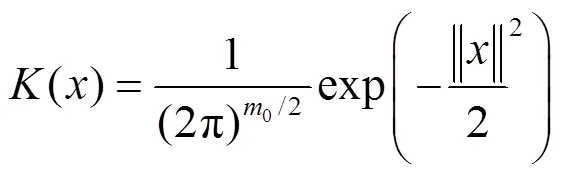
采用上述训练样本对网络进行训练，在训练之前需对样本数据归一化预处理，即变换到[-1，1]范围内，这样处理的好处在于可以加快收敛速度、防止大样本吞并小样本以及奇异样本数据的影响。

2.3 钟差预报步骤

根据以上分析，钟差预报的实施步骤可简述为：

2）将步骤1的预报值和对应的观测值组成训练样本，并对其归一化处理；

4）对网络输出值作逆归一化处理，即将输出变量还原到原来单位。

3 算例分析

为了验证本文模型效果，从http://igscb.jpl.nasa.gov/components/prods.html网站上下载了2010年12月12日的IGS精密GPS卫星钟差数据，采样间隔为5 min，选取PRN08和PRN20卫星的钟差数据进行实验，并与线性组合模型的预报精度进行对比分析。需要说明的是，这2颗卫星携带的原子钟分别为Cs钟和Rb钟，其当天的钟差变化如图2所示。线性组合预报模型为

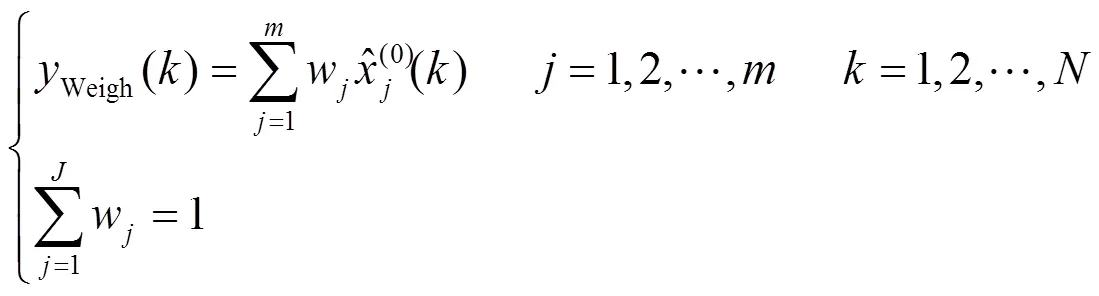
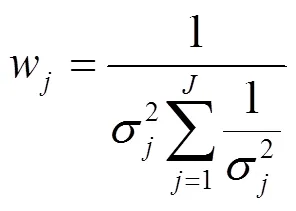
图2 原始钟差数据

当对初始值作不同的取舍时，所建GM（1，1）模型也就不同，因此，3.1节分析了不同初始历元个数对灰色系统模型预报精度的影响，3.2节对线性组合模型与本文模型的预报精度进行了比对分析。通过上述分析，验证本文提出的混合预报模型在钟差预报时的可行性和有效性。

3.1 单纯GM（1，1）模型预报

分别取12个历元（01:00:00～01:55:00）、18个历元（00:25:00～01:55:00）和24个历元（00:00:00～01:55:00）的钟差值建立GM（1，1）模型，分别记为GM12、GM18和GM24，并分别用上述3个模型对2组钟差序列进行6 h的预报（02:00:00～07:55:00），其预报误差（预报值与观测值的差值）如图3所示。

从图3可以看出，不同GM（1，1）模型的预报精度存在一定差别，对于PRN08卫星钟差而言，灰色模型的预报精度从高到低依次为GM12、GM24、GM18；而对于PRN20卫星钟差，从高到低依次为GM24、GM18、GM12，这就是说参与建模的初始值历元个数对预报精度有重要影响，而实际应用时往往不清楚选取多少个初始值建模最为合适，即哪个模型是最优的事先并不知道。

图3 灰色系统模型预报误差

3.2 线性组合模型与本文模型预报精度对比分析

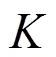
结合图1，分析表1可以看出，线性组合模型和本文模型都能有效地组合单一灰色系统模型的预报结果，但预报精度存在一定的差别。对于2种组合模型的具体特征总结如下：

1）线性组合模型至少是一种非劣组合，即组合预报的各项误差统计指标，包括最大值、平均值和均方根误差，均不大于由单一模型预报得到的对应项的最大值。该方法较为容易实现，简单实用；

2）无论是预报误差的最大值、平均值还是均方根误差，灰色神经网络模型的统计结果均优于单一的灰色系统模型，也优于线性组合模型，这说明灰色神经网络模型是一种优组合，即预报结果好于任一种单一模型。该模型对样本数据的依赖性高，要求样本数据能覆盖钟差序列的系统特征。

图4 灰色系统及其线性组合与本文模型预报误差

表1 预报误差统计 ns

4 结语

本文所提出的基于灰色系统和神经网络组合的钟差预报模型，利用了灰色模型GM（1，1）要求原始数据少，方法简单的特点，构造了多个不同的GM（1，1）模型，同时借助神经网络强大的非线性映射能力，将这些不同的模型进行非线性组合，不仅避免了模型选择的盲目性，也提高了钟差预报的精度。另外，试验表明该模型优于基于经典加权方法的线性组合灰色模型。

[1] 吴海涛, 李孝辉, 卢晓春, 等. 卫星导航系统时间基础[M]. 北京: 科学出版社, 2011: 62-63.

[2] 陈小敏, 李孝辉. 基于自适应Kalman滤波的原子钟信号预测方法[J]. 吉林大学学报: 理学版, 2009, 47(3): 591-593.

[3] 李变, 屈俐俐, 高玉平. Kalman算法在原子时计算中的应用研究[J]. 时间频率学报, 2010, 33(1): 11-15.

[4] 王尔申, 张淑芳, 胡青. 基于时钟偏差模型的GPS不完整星座定位方法[J]. 大连海事大学学报, 2009, 35(2): 59-61, 64.

[5] 郑睿, 陈杰. 信号短暂缺失下的非完备GPS定位算法研究[J]. 电子科技大学学报, 2009, 38(4): 496-500.

[6] 黄继勋, 周立弦, 范跃祖. 时钟偏差辅助的GPS完整性监测算法[J]. 北京航空航天大学学报, 2001, 27(2): 161-163.

[7] 许龙霞, 李孝辉. 基于接收机钟差的GPS完好性自主监测算法[J]. 宇航学报, 2011, 32(3): 537-542.

[8] 崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报: 信息科学版, 2005, 30(5): 447-450.

[9] 路晓峰, 杨志强, 贾小林, 等. 灰色系统理论的优化方法及其在卫星钟差预报中的应用[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 492-495.

[10] 史德明, 李林川, 宋建文. 基于灰色预测和神经网络的电力系统负荷预测[J]. 电网技术, 2001, 25(12): 14-17.

[11] 马锐. 人工神经网络原理[M]. 北京: 机械工业出版社, 2010: 8-9.

[12] 李孝辉, 柯熙政. 原子钟信号的神经网络模型[J]. 陕西天文台台刊, 2001, 23(2): 110-115.

[13] 周敏, 李世玲. 广义回归神经网络在非线性系统建模中的应用[J]. 计算机测量与控制, 2007, 15(9): 1189-1191.

[14] 范国清, 王威, 郗晓宁. 基于广义回归神经网络的电离层VTEC建模[J]. 测绘学报, 2010, 39(1): 16-21.

[15] 丁常富, 王亮. 基于交叉验证法的BP神经网络在汽轮机故障诊断中的应用[J]. 电力科学与工程, 2008, 24(3): 31-34.

Clock bias predicting based on grey system and neural network

LEI Yu1,2,3, ZHAO Dan-ning1,3,4, GAO Yu-ping1,2

(1. National Time Service Centre, Chinese Academy of Sciences, Xi′an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, National Time Service Center,Chinese Academy of Sciences, Xi′an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100039, China; 4. Key Laboratory of Precision Navigation and Timing Technology, National Time Service Center, Chinese Academy of Sciences, Xi′an 710600, China)

For avoiding the weakness of single model in predicting clock bias, a hybrid method combining the grey model(GM) and neural network(NN) for predicting clock bias is proposed. The basic idea, prediction model and practical process of clock bias predicting based on GM(1,1) and GRNN(generalized regression neural network) are presented. In view of the defects of traditional NN, the-fold cross-validation algorithm is employed for improving the generalization ability of GRNN. For verifying the feasibility and validity of the hybrid method, the clock bias predictions are carried out by using the real data of GPS satellites clock bias and the prediction precisions for different methods are compared. The results show that the prediction precision for the proposed method is better than those for the GM(1,1) and the weighted combination of GM(1,1).

grey system; neural network; clock bias prediction

P228.4

A

1674-0637(2013)03-0156-08

2012-10-15

国家自然科学基金资助项目（10573019）

雷雨，男，博士研究生，主要从事GNSS时间传递方面研究。