新型混接式脚手架极限承载力研究＊

周 盛 李 瑞 汪 洋

（武汉理工大学能动学院1） 武汉 430063） （大连理工大学船舶工程学院2） 大连 116024） （大连中远船坞工程有限公司3） 大连 116113）

0 引 言

本文的研究对象是一种用于LNG 船内舱建造的新型脚手架，其主要特点是杆件先通过焊接形成若干组件，组件之间再通过插销连接成脚手架，这种混合连接方式使其力学性能不同于传统脚手架，其中脚手架的极限承载力与稳定性一直是人们最关心的问题.徐崇宝等提取双排脚手架进行了理论分析和试验研究，得到多层多跨空间框架节点刚性处理时，不同约束情况下的整体屈曲特征值和屈曲模态［1］.敖鸿斐对双排脚手架整体稳定极限承载力提出了通用计算方法［2］.Weesner和Jones对4种不同形式的高承重脚手架在足尺寸下的极限承载力进行试验研究，运用有限元法计算得到了脚手架分支形屈曲和极值点屈曲的分析结果［3］.Godley研究了扣件式钢管脚手架的二维与三维模型对计算刚度的影响程度，分析节点半刚性对脚手架动力特性研究的重要性［4］.

以上这些研究成果为不同类型的脚手架失稳分析提供了丰富的基础理论与计算方法.本文通过有限元法计算该混接式脚手架的极限承载力，评估其稳定性：首先计算该脚手架的4种主要失稳形式以及各种失稳形式下的极限承载力；之后分析脚手架极限承载力的主要影响因素，其中包括：立杆纵距、立杆步距、步数，以及连墙件位置；最后与同尺寸扣件式脚手架比较极限承载力的不同.本文的研究成果将为该类混接式脚手架的使用与维护提供理论依据.

1 脚手架极限承载力理论计算方法

插销式钢管脚手架主要是靠框架立杆轴心受压将竖向荷载传给基础.所以，插销式钢管脚手架主要受轴向压力，虽有弯矩作用，但所产生的附加应力不大.因此压杆的稳定很大程度上决定了脚手架的承载力的大小.对于端部有约束（包括铰接、刚接、半刚接和自由端）的轴心受压构件可以用下述方法来其确定其极限承载力［5］.

如图1a）所示，构件上端和下端弹性的抗弯弹簧常数分别为rB和rA，而上端平移的弹性弹簧常数为kR.构件的变形和作用于构件两端的力见图1b），在图中以顺时针的转角为正，以右的平移为正，柱端的力矩和水平力以与位移同方向时为正，异向时为负.取图1c）所示的隔离体，建立力矩和与x 轴相垂直的水平力的平衡方程

图1 端部有约束的轴心受压构件

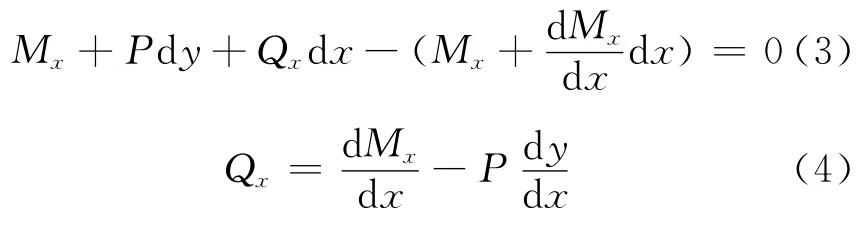
以式（4）代入式（2）后，得

由式（4）又得到横向力

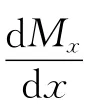
通解中的4个积分常数可由构件两端的集合边界条件和自然边界条件确定，它们的表达式都可以用与构件的挠度y 有关的量来表示：（1）铰接端，y＝0，Mx＝0或y＇＝0；（2）固定端，y＝0，y＇＝0；（3）自由端，Mx＝0或y＇＝0，Qx＝0或y＇＋k2y＇＝0；（4）上端只有平移的弹性约束，y＇（l）＝0，Q（l）＝－PC3＝－kBy（l）；（5）上端只有转动的弹性约束，y（l）＝0，M（l）＝－EIy＇（l）＝rBy＇（l）；（6）上端有平移的弹性约束同时还有转动的弹性约束，－C3P＝－kBy（l），－EIy＇（l）＝rBy＇（l）.

根据构件两端的4个独立的边界条件可以建立4个线性齐次方程，组成如下线性方程组

式中：a11，a12，…，a44均是取决于两端边界条件的系数.由于式（13）中没有常数项，因此C1，C2，C3，C4有非零解的条件是系数行列式为零，即

由于在式（14）中只有未知量k，所以P＝k2EI，从而可以解得P.但是式（14）的展开式是一个超越方程，适合此方程的解可能有很多个，应取其中的最小值为屈曲载荷Pcr.由于以上计算方法无直接的理论联系，本次研究将不采用这种方法，而是采用软件进行模拟节点销接处理，来求得理想的弹性屈曲荷载的方法.

2 脚手架有限元建模

2.1 脚手架模型

本文从脚手架整体中选取一个双排六步三跨的局部结构进行有限元建模，单元选用Ansys中的Beam188 三维梁单元.立杆步距（立杆高度）2.8m，纵距（2立杆间纵向X 距离）2.5m，横距（2立杆间横向Y 距离）2m.图2为脚手架及其基本组件的有限元模型.组件之间的销接节点通过耦合自由度的方式模拟，组件内部的焊接节点则通过共用节点的方式模拟，通过两者的结合来模拟该脚手架的混合连接方式.

图2 脚手架有限元模型

脚手架所用材料为低碳钢Q235，常温下的材料特性见表1.垂向立杆为薄壁构件，截面为空心方框，外边长为80mm，厚度为5mm.

表1 构件材料特性

2.2 基本假设

应用有限元法，计算该脚手架的失稳形式与极限稳定承载力时，采用的假设有：（1）线弹性假设，脚手架各立杆与梁的轴线都在同一平面内；（2）数值相等的竖向集中荷载作用于框架顶层的各节点上；（3）忽略地震荷载、风荷载，以及动力载荷的影响；（4）在同一层中各立杆会同时发生屈曲.

3 失稳形式与极限承载力分析

3.1 各种失稳形式与极限承载力

分析该脚手架结构的前4阶屈曲模态，计算脚手架在各阶失稳状态下的极限承载力，见表2.

表2 不同失稳形式下的极限承载力

典型的1 阶失稳最先发生在底层，见图3a）.3阶失稳最先发生在第二层，向上下延伸，只有半个波形，见图3c）.4阶失稳最先发生在中间层，出现2个完整的正弦波形，见图3d）.前2阶屈曲模态属于局部失稳，后2 阶属于整体失稳.

3.2 极限承载力影响因素

1）立杆纵距与步距的影响 取一系列的立杆纵距和立杆步距，分别计算该脚手架的极限承载力值，见表3～4.

图3 4种失稳形式比较

表3 立杆纵距变化时极限承载力值

表4 立杆步距变化时极限承载力值

可以看出，极限承载力随着步距和纵距尺寸的增加呈下降趋势.通过比较下降趋势，可以发现：步距对极限承载力的影响要大于纵距的影响.

2）步数的影响 表5所列为不同步数下的极限承载力，随着步数的增加，脚手架的极限承载力不断减小.

表5 步数变化时极限承载力值

3）连墙件位置的影响 连墙件三步一设和两步一设时的极限承载力分别为197kN 和236 kN，比连墙件只设在顶部时的157.6kN 分别大25%和50%，说明连墙件的设置能够大幅提高脚手架结构的极限承载力.屈曲模态图见图4～5，可以发现连墙件能有效防止连墙件以上的各层发生屈曲.值得注意的是这些连墙件都设置在结构较弱的横向位置，对于纵向作用不大.

图4 连墙件两步一设

图5 连墙件三步一设

3.3 承载力比较

根据文献［6］中所列出的立杆的稳定性公式算得同尺寸下扣件式脚手架的极限承载力为86.4 kN，与该混接式脚手架时的一阶弹性屈曲极限承载力值157.6kN 进行比较，发现该类脚手架的极限承载力超过扣件式脚手架82%，值得推广使用.将极限承载力除以立杆的截面积1500mm2，折算成钢管所受的压应力为105.1 MPa，而材料Q235的屈服强度为235MPa，故此结构在材料未达到屈服强度时已发生屈曲.

4 结 论

1）脚手架失稳有多种形式，通常失稳是沿它的横向发生破坏的；该脚手架的失稳主要发生在第一层和第二层，应对这2层进行加固处理.

2）脚手架与墙的横向拉结有助于整体稳定性的提高；立杆纵距增大时，极限承载力减小趋势近似线性，立杆步距增大时，极限承载力呈非线性减小.

3）通过对比得出该脚手架极限承载力比扣件式脚手架高出82%.当屈曲发生时，材料尚未屈服.

［1］徐崇宝，张铁铮，潘景龙，等.双排扣件式钢管脚手架工作性能的理论分析与实验研究［J］.哈尔滨建筑工程学院学报，1989，22（2）：39－44.

［2］敖鸿斐.双排脚手架整体稳定极限承载力通用计算方法［J］.施工技术，2005，34（3）：39－41.

［3］WEESNER L B，JONES H L.Experimental and analytical capacity of frame scaffolding［J］.Engineering Structures，2001，23（6）：592－599.

［4］GODLLEY M H R，REALE R G.Sway stiffness of scaffold structures［J］.Structural Engineer，1997，75（1）：4－12.

［5］陈 骥.钢结构稳定理论与设计［M］.北京：科学出版社，2011.

［6］王玉龙.扣件式脚手架计算手册［M］.北京：中国建筑工业出版社，2008.