拟合法兰零件数控加工编程与优化

中航工业空空导弹研究院凯迈机电公司（河南 471003）刘仁春 袁维涛

宏程序本身的篇幅不大，但是在数学表达上却有相当难度。为了更容易理解，这里以我公司的零件“拟合法兰”为例，分析编写宏程序时的编程步骤和基本思路以及宏程序的用法。

利用Pro/E建立的模型，如图1所示。

图1

1.零件分析

本零件是圆柱体的一端均布4个由螺旋形斜面和台阶组成的齿，类似端面凸轮，展开后，每个齿都是由一段斜线和上下两条直线段组成，中间用R20mm圆弧过度连接。通过对本零件分析，精加工可以选用带转台的四轴数控铣或三轴数控铣床加工，无论哪种机床都要一刀一刀的逼近零件轮廓。虽然本零件在四轴机床上可以加工，但是，此类零件是根据用户需要定制的，所以批量小，尺寸经常需要更改，根部的R圆弧倒角有时很小甚至没有。当R很小时，用带四轴的转台加工，就无法满足要求。而在三轴数控铣床上用立铣刀精加工此端面，则不存在以上问题。零件的装夹定位，用圆柱心轴和压板定位压紧。坐标系设定在圆柱中心，Z轴零点设在齿形底部。走到路线为用立铣刀由外往内，每圈从齿形底部往顶部切削。选用FANUC 0i数控系统。以下以第四象限的齿为例，阐述宏程序的编写步骤。

（1）刀具选择 本零件可以用球头铣刀或立铣刀，但考虑到齿形根部有时没有R倒角，球头刀不能满足要求，并且为了做一个通用的宏程序，而立铣刀可以不受倒角R的限制。确定选用立铣刀加工此类零件。下面计算能选用的刀具尺寸。根据零件的形状可知，刀具最容易在拟合齿内圈边沿的底部和90°立面发生干涉。所以按内圈尺寸展开进行计算，然后还原到相应的圆柱面上即可。如图2所示。

图2

把尺寸L3还原到半径为40mm的圆柱面上，因为

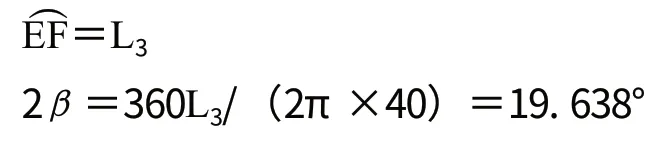
刀具半径r＝EO2＝40tanβ＝6.92mm，我们就可以选用半径小于6.92mm的立铣刀。

（2）计算步距 下面根据零件允许的残留高度计算步距。同样，把零件展开如图3所示。根据斜面角度来进行步距计算，其原理如图3所示。立铣刀在斜面N上留下的痕迹在M面上是椭圆的一部分，该椭圆的长半轴a＝D/2（铣刀半径），短半轴b＝（D×sinα）/2，其方程为：

根据取之M界面图的已知变量和椭圆方程，可以计算出（见图3）：

图3

由上式可看出α越大，残留高度越高；K不变，立铣刀越大，残留高度越小；D不变，K越大，残留高度越大。所以选用φ12mm铣刀，并以内圈为基础计算，根据图2可知α＝18.87°。根据上式可推算出以下公式：

设δ＝0.01mm，则代入计算K≈1.216，取K＝1.2。

2.数学计算

编写数控程序除了有加工经验，更重要的还要有数学计算的能力，特别是编制宏程序时，数学计算更为重要。以下计算坐标时，为了避开多元高次方程组求根的情况，尽量运用了直角三角形的勾股定理和三角函数性质。并且图4中计算的尺寸都使用宏程序所用到的变量代表。

根据图样已知变量有：

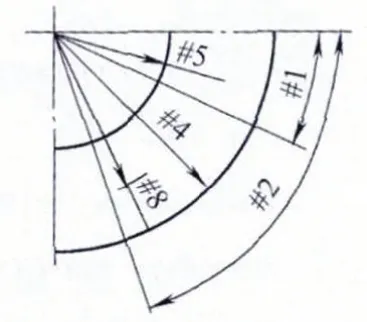
图4

借用数控系统的插补原理，以下计算都是随#8圆柱体的齿形半径自变量和#30倒角R的角度自变量的变化而变化的，所以只能给出各个变量之间的关系，没有具体数值。在运行程序时只要给#8一个具体的数值，其他变量自动就计算出数值。

图5

图5是在圆柱体的齿形半径内任取一半径值为#8，并把在相应的半径下的圆柱面展开所得到的局部展开图。Q点即是#1角度处斜面和底面的交点。

根据四边形性质，可知∠AOB＝#10,在∠AOB任取一角度∠A OC为#30的自变量（从0变化到#10）。计算C点的值：

以上数值是零件轮廓的轨迹，下面把刀具半径#7加进示意图中，如图6所示，刀具中心相对于Q点的距离为#17＝#12－#16＋#7。

图6

#15结果不变。下面再把结果还原到相应的圆柱面上的到极坐标是：极半径不变仍是#8；极角是：

然后从极坐标分别转换成X、Y、Z各轴坐标的值：

#2角度处斜面和顶面相交处各点的计算方法和上面#1角度处的计算方法基本一样，为了简化编程，相同的位置还使用相同的变量表示。如图7、图8所示。

图7

图8

同样使用#30的自变量（只是为了保证连续切削#30从#10变化到0）。计算D点的值

同样考虑上刀具半径#7，刀具中心相对于P点的距离为： #17＝#12－#16－#7

同理把结果还原到相应的圆柱面上的到极坐标是：及半径不变仍是#8；

极角是： #28＝#2＋#17/（2π×#8）×360°

然后从极坐标分别转换成X、Y、Z各轴坐标的值：

3.程序编制

根据以上的理论计算，只需把数学计算转换为数控语言，再在合适的位置，加上控制程序分支、循环的指令。另外在细节上，再加入一些能够正确控制变量计算的方法，就可以编制出一个完整的宏程序。程序如下：

4.Vericut模拟验证并加工零件

Vericut是进行数控程序模拟、仿真、验证和优化的软件。它可以替代我们检验3～5轴NC程序运行过程,还可以用设计模型与仿真加工模型的比对功能，定量分析仿真加工模型。选用相应的数控系统和机床类型，利用Vericut的自动对比功能，将宏程序加工的零件和Pro/E建立的模型对比，符合图样要求。

最后将编好的程序在数控机床上进行加工，得到了合格的产品。