扭矩对塔机塔身主弦杆受力的影响

文朝辉，王永新

WEN Chao-hui,WANG Yong-xin

(1.湖北江汉建筑工程机械有限公司，湖北 荆州 434024；2.山东电力建设第一工程公司，山东 济南 250131)

1 概 述

塔机按结构组成可分为金属结构、工作机构和驱动控制系统三大部分。金属结构作为整机的骨架，是塔机的重要组成部分，起重机的各种工作机构及零部件安装或支承在金属结构上，承受着起重机的自重以及各种工作状态和非工作状态的外载荷，耗钢量大，通常其重量占整机重量的一半以上。

塔身是金属结构中的重要组成部分，无论是水平臂式塔机，还是动臂式塔机，在整机自重和成本中占有很大比重，尤其是大吨位和起升高度高的塔机，塔身所占的比重更大，因此如何对塔身的结构进行合理计算，降低塔身重量，对降低塔机成本具有重大意义。

在对塔身主弦杆进行设计计算时，一般认为影响主弦杆内力的主要因素只有弯矩和轴向力，而扭矩对主弦杆的影响忽略不计，但是在对某些常见结构型式的塔身进行有限元计算时，可以看出扭矩不仅使主弦杆产生附加应力，而且此应力所占的比例较大，不能忽略不计。本文以最常见的某型号塔机塔身为例，比较扭矩对主弦杆受力的影响。

2 塔身主弦杆的计算

塔机结构型式很多，最常见的为截面为矩形的空间格构式结构。格构式塔身一般都是采用平面分析方法，即把空间桁架分解为平面桁架进行内力分析，具体做法是把塔身分解为几个平面桁架组成的空间桁架结构，然后将各载荷分别分解到每一个平面桁架上，先单独地计算各平面桁架的杆件内力，然后再把同一杆件的内力叠加起来，作为验算塔身强度、刚度和稳定性的主要依据。

任何型式的塔身都必须计算其强度、刚度和稳定性等共性问题。外载荷在各种工况下对塔身的作用，最终都可以归纳为直接作用的横向力、轴向力、弯矩和扭矩。

若不需要求出每一根杆件的内力，只需在进行危险截面验算时，可不将外载荷进行分解，对于正方形截面塔身，腹杆内力主要是平衡截面剪力和扭矩，而主弦杆的内力主要是平衡截面弯矩和轴向力。所以可先根据外载荷求出截面上的弯矩M 及轴向力V，然后求得主弦杆内力

以某型号塔机为例进行比较计算，其塔身截面1500×1500mm（中心距），高度为2500mm，主弦杆为135×10 方管，斜腹杆为70×5 方管，水平杆50×5 方管。外载荷：扭矩Tn=28tm，倾翻力矩M=130tm，轴向力V=45t。

2.1 公式计算

倾翻力矩简化为塔身45°方向力偶时，塔身主弦杆轴力最大。

单根主弦杆最大受力

2.2 有限元计算

为简便起见，只针对一节塔身标准节建立有限元模型，如图1 所示，单元类型均为梁单元，只加载倾翻力矩和轴向力而不加载扭矩，倾翻力矩M 简化为塔身45°方向的力偶（图2）。

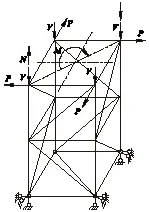
图1 塔身标准节有限元模型

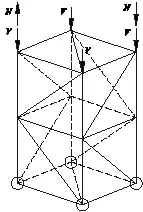
图2 倾翻力矩和轴向力加载图

经计算，若只加载倾翻力矩和轴向力，其主弦杆最大轴力为706kN，此值和2.1 公式计算的结果710.8 kN 极为接近，相差仅0.6%，说明不加扭矩公式计算和有限元分析结果基本一致。

如果加载扭矩进行计算（图3），其主弦杆最大轴力为804kN，此值和式计（1）算的结果710.8 kN 相差93.2kN，达13.1%。

3 结 语

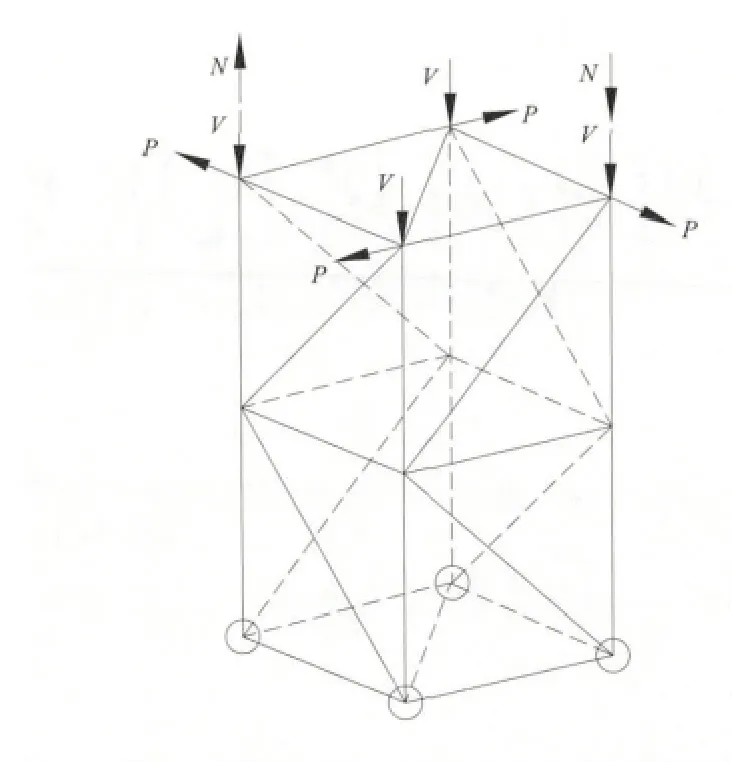
图3 倾翻力矩、轴向力和扭矩加载图

从以上计算分析可以看出，对于塔机塔身主弦杆的计算，如果公式计算时对扭矩的影响忽略不计，但在进行有限元分析时，加载扭矩后其计算结果和公式计算有很大出入，造成这个差异的主要原因是公式计算是把塔身简化成桁架结构计算，而有限元分析则是简化成更加符合实际情况的钢架结构，在某些情况下，这种简化有很大的差别，因此不考虑扭矩对主弦杆的受力影响是不合理的。

值得注意的是，扭矩对塔身主弦杆受力的影响和腹杆布置的形式有很大关系，除本文所述腹杆布置形式外，在对某些其他腹杆布置形式的塔身计算时，公式计算和有限元分析的结果相差不大，而本文所述的腹杆布置形式的塔身恰恰是目前最常见的，因此应引起设计者足够的重视。

[1]侯宝佳，毛居双.塔机塔身结构设计方法的比较［J］.建筑机械化，2006，（07）：31-36.

[2]薛 渊，陆念力.塔机塔身扭转刚度的比较[J].建筑机械，2005，(08)：74-76.

[3]曹俊杰.塔机塔架的扭转计算—对苏联《建筑用塔机》一书中扭转公式的探讨［J］.工程机械，1985，（11）：37-43.

[4]徐乃祥.固定式塔机的扭转变形计算[J].建筑机械，1985，（02）：22-25.