基于遗传算法智能组卷的考试系统设计及实现＊

张烈超 刘开文

（武汉交通职业学院，湖北 武汉 430065）

智能化组卷策略是网络考试系统的核心技术，也是实现网络考试系统的重点和难点。智能组卷遇到的主要问题是保证生成的试卷具有随机性、合理性、科学性的同时，必须最大程度地满足用户的需求，如诊断、评估考生的知识、能力掌握情况，提高考试的信度和效度。因此，在网络交互环境中，题库试题质量要求比较高的前提下，组卷算法设计的优劣直接决定了其执行效率及质量，故而选择一个高效、科学算法是智能组卷的关键。［1］

组卷问题的实质是一个在一定约束条件下的多目标参数优化问题，它的约束条件难以用数学形式来描述，采用传统的数学方法求解十分困难。［2］文献［1］［2］中提到的 随机选取法和回朔试探法等组卷策略在求解大量试题或者复杂度较高的问题时有明显的缺陷，而采用人工智能算法之一的遗传算法，求解此类组卷问题则取得了较好的效果。［3］本文利用遗传算法作为求解智能组卷问题的策略，应用于考试系统，并取得了较好的效果。

1 智能组卷相关问题

1.1 试卷构成要素

智能组卷考试系统中需要考虑的一项重要的内容就是：如何从现有的试题库构建满足教学要求的试卷。通常情况下，构成一套试卷需要考虑很多因素，而且试卷中的每一道试题又包含多个属性，其中，与组卷有关的属性可能有以下几项内容：（1）题型；（2）知识点；（3）试题难度系数；（4）总分。［4］组卷过程中，由上述几个属性共同决定题库中某道题目能否被抽中。生成一份n道题的试卷就是从试题库用智能算法抽取n道符合要求的n道题，组成一个n×4的矩阵，矩阵中的每一列代表一个属性，每一行代表一道题。［5］

该矩阵应满足以下约束条件：（1）题型：为考察学生的思维水平、分析运算以及科学表达等能力，一份试卷应包含足够的客观性试题及一定数量的非客观性试题。综合考虑上述两方面的要求，本课题设计的试题库包含了单选题、多选题、判断题、填空题、综合题等题型；（2）难度：针对不同考试对象及不同阶段的考试，设置不同的难度，但应保证试卷的区分能力。将试题按照容易（0.1～0.4）、中等（0.5～0.7）、难（0.8～0.9）三个难度等级［6］加以区别，此外试卷的难度系数为该套试卷所有题目分数＊难度系数／总分；（3）分数：每套试卷的分数为100分，另外，对于综合题型在保持总分不变并采用随机确定分数，可以加快算法收敛及题目的分配策略；（4）知识点：考试的内容领域涉及多个知识点，每个知识点可对应多道题型，并采用随机方式选择相应的知识点并保证一定的覆盖率，特别是重点内容的覆盖。

1.2 数学模型

智能组卷系统能客观抽出符合要求的试卷，需要用户预先设定目标试卷（理想试卷）评估标准。遗传算法常引入适应度及相关的函数来进行评判手段，适应度是驱动遗传算法不断寻优的动力，适应度函数用来评判试卷种群中个体的优劣程度的关键指标，针对试卷的题数，总分等要求在初始化种群时已经预先考虑，此处只需考虑知识点分布及难度系数。适应度函数跟知识点分布及试卷难度系数有关，相关评判函数如下：

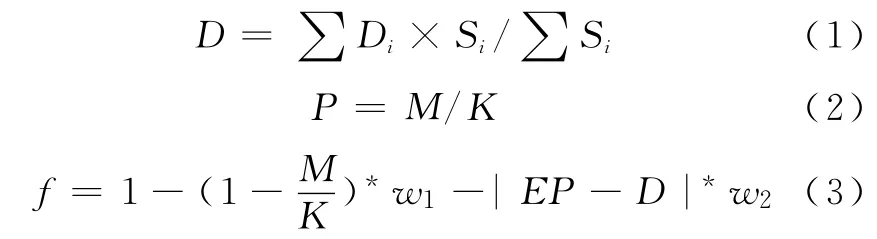
上述（1）式为试卷难度系数公式，其中i＝1，2……K，K是目标试卷所含的题目数，Di，Si分别是第i题的难度系数和分数；（2）式为知识点覆盖率计算公式，例如，考试的内容领域包含K个知识点，而一个个体（即待评的试卷）中所有题目知识点的并集中包含M个（M≤K），则知识点的覆盖率为M／K；（3）式为适应度评判函数，此处适应度函数跟知识点分布［即（2）式］及试卷难度系数［即（1）式］有关。其中，EP为用户的期望难度系数，D为试卷难度系数，w1为知识点分布的权重，w2为难度系数所占权重。当w1＝0时退化为只限制试题难度系数，当w2＝0时退化为只限制知识点分布。由评判目标可知，用户的期望难度系数与试卷难度系数之差越小越好，试题知识点覆盖率越大越好。

1.3 遗传算法

遗传算法（Genetic Algorithm，简称GA）是一类借鉴生物界的进化规律演化而来的非数值模拟的计算模型，利用优胜劣汰的自然遗传机制，使种群中的个体不断朝着最优解的方向移动，最终搜索到问题的最优解，常用来解决多约束条件下的最优问题。［7］

遗传算法执行的特点是从代表问题可能潜在的解集的一个种群开始的，通过编码，产生初始种群，再予以遗传、交叉、变异操作，并对每个染色体通过适应度评判函数进行评估。遵循适者生存的原理，利用“优胜劣汰”的自然选择机制，不断进行迭代以产生新解或称新个体，通过不断进化，使种群中的个体不断朝着最优解的方向移动，最终搜索到问题的最优解。［8］

由于遗传算法具有内在的并行性，可有效解决模型计算量大的问题。因此，遗传算法非常适合处理试题库智能组卷问题。［9］

1.4 遗传算法实施流程图

算法实施流程如图1所示：

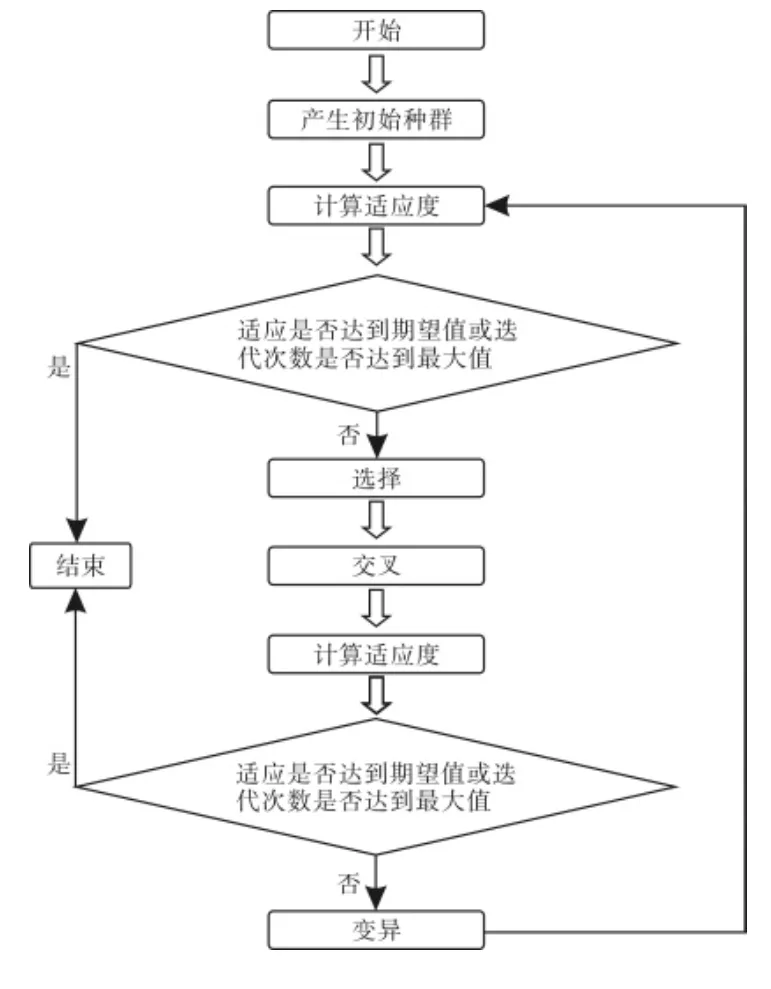
图1 算法实施流程图

2 遗传算法在智能组卷中的解决思路及实现

利用遗传算法进行自动组卷是根据出卷者给定的约束条件（本课题仅考虑试卷以下的属性：题目数量、试卷总分、试题知识点分布、试题难度系数、试卷题型比例等），搜索试题库中与出题要求相匹配的试题，从而抽取符合目标要求的试题组合。

本课题为通过遗传算法抽题策略的系统，因此，涉及到数据库技术的试题库建立和维护，此处略去该过程，集中讨论遗传算法抽题思路，由于遗传算法在执行过程中涉及到编码、产生初始种群，遗传操作（选择、交叉，变异）、适应度函数的条件的判别等步骤。

用遗传算法实现组卷算法如下：

2.1 染色体编码

用遗传算法求解问题，首先要将问题的解空间映射成一组代码串，即染色体的编码问题。

此处对染色体编码采用了自然数编码策略：即根据组卷要求从题型库中选出试题组成符合要求的染色体基因段。基因编码直接采用试题的编号。基因个数要求与组卷初始设置试题的个数保持一致，并且各题型组之间的编码是要求相互独立的。这样染色体无需解码，经过迭代优化之后可直接生成目标试卷，［10］每一组编码反映一种题型。每个染色体即为一套试卷，无需再进行二进制至十进制编码的转换。

编码方式具体如下［11］：构建试卷，将试卷与染色体对应，试卷中每道题的题号组成染色体的基因编号，题型相同的试题放在一起，不同的题型经过分组后再按照染色体分段编码规则组成分段基因序列，在后续的遗传操作时也按此规则进行，从而保证了每种题型的题目总数不变。如要组一份试卷，包含客观题（单选题6道，多选题4道），主观题型（填空题5道，判断题5道，综合题3道），则采用自然数编码染色体结果如下：

2.2 初始种群的确定

确定初始种群（分试卷种群）的大小，种群规模的大小可以按问题需求予以设计。此外，结合试题库总题数、编码题型比例、总分等要求，采用不完全随机的方法生成试卷初始种群，使得初始种群一开始就满足了题数、总分等要求，并在初始处理阶段对相关题型采取随机给定分数值，这样可加快遗传算法的收敛并减少迭代次数。初始种群代码如下：

2.3 选择操作

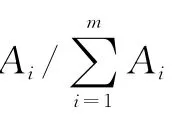
2.4 交叉操作

遗传算法中起核心作用的是遗传操作的交叉算子。所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。由于本算法设计编码采用的是自然数编码，所以在进行交叉时采用分段单点交叉（按题型分段来进行交叉）。交叉过程需要注意，一是要保证试卷总分不变，二是保证交叉后没有重复题号。交叉操作算法如下：

2.5 变异操作

变异操作在遗传算法中起全局搜索的作用，变异概率一般较小。具体方法是对种群中的个体（染色体）串的某些位置上的基因作变动。［13］本算法没有采取将染色体分段进行变异，而是根据算法条件中的要求对染色体某段内的某个基因进行变异。变异基因的选择原则［14］为：与原基因所代表的题型相同、分数相同，至少包含原题目一个有效知识点（与期望试卷知识点保持一致）。变异操作算法如下：

3 网络考试系统体系结构设计及应用

3.1 智能组卷算法应用

用java语言实现遗传算法并将其嵌入本课题的应用系统（B／S结构）作为抽题策略、以试题库（基于mysql数据库）中210道试题作为数据源，并给出要生成的试卷要求，利用遗传算法进行抽题。算法中的参数分别为最大演化代数：500，适应度期望值为0.98，试卷难度系数：0.55，试卷总分：100，每套试卷试题数44。随机抽取的1套试卷如下：

此外，通过组卷算法生成的试卷可用于无纸化考试，也可用于传统考试备用试卷。

3.2 考试系统体系结构设计及功能

考试系统功能主要包括试卷维护、抽题组卷、学生考试、考试分发、考试管理、阅卷、成绩统计等。考试系统体系结构如图2所示，相关模块功能如下：在前期建立的试题库中使用遗传算法生成的试卷作为无纸化考试或传统考试的试题源（为防止考生作弊现象，可采取生成多份试卷策略）；教师或者考试管理员通过考卷分发模块随意为参加考试的考生分配考卷；准予参加考试的考生登录系统后可以进行在线考试；考试管理模块可对考试过程进行实时监控并将相关信息存入数据库中；考试结束后，教师通过阅卷模块进行评分，并可统计成绩；考生可对个人考试成绩进行查询。

图2 考试系统体系结构

4 结语

本文设计了一种基于三层架构的网络考试系统结构，采用基于自然数编码的遗传算法智能化组卷策略，并将算法应用于网络考试系统中［15］。实验结果表明，用遗传算法能有效的解决自动组卷问题，具有较好的使用性能和实用性。

本算法尚需进一步深入研究，如引入相关机制对抽题过程中算法可能出现的过早收敛或者陷于局部优化的情况加以改进，有望取得更好效果。

［1］［5］朱玉祥，苗春生，孙承佼.基于算法的试题库智能组卷系统研究［J］.南京气象学院学报，2006，（2）：282－285.

［2］［6］［9］［10］［12］［13］周文举.基于遗传算法的自动组卷系统研究与实现［D］.山东师范大学硕士学位论文，2006：6－16.

［3］全惠云，范国闯，赵霆雷.基于遗传算法的试题库智能组卷系统研究［J］.武汉大学学报（自然科学版），1999，（5）：758－760.

［4］杨青.基于算法的试题库自动卷问题研究［J］.济南大学学报（自然科学版），2004，（3），228－231.

［7］Guo Tao，Kang Li－shan.A new Evolutionary Algorithm for Function Optimization［J］.Wuhan University Journal of Nature Sciences，1999，（4）：409－414.

［8］J.T.Tsai，T.K.Liu，J.H.Chou.Hybrid Taguchi－Genetic Algorithm for Global Numerical Optimization［J］.IEEETransactions on Evolutionary Computation，2004，（4），365－377.

［11］［14］实例讲解遗传算法——基于遗传算法的自动组卷系统［EB／OL］.（2011－05－19）［2013－01－12］.http：／／www.cnblogs.com／artwl／archive／2011／05／19／2051556.html.

［15］拓守恒.基于遗传算法智能组卷的J2EE考试系统的设计与实现［J］.西华大学学报（自然科学版），2010，（5）：31－37.