基于模糊PI复合控制的异步电机矢量控制系统仿真*

周凌华(武汉交通职业学院,湖北 武汉 430065)

基于模糊PI复合控制的异步电机矢量控制系统仿真*

周凌华
(武汉交通职业学院,湖北 武汉 430065)

针对常规的矢量控制的方法使得电机因参数变化和非线性因素影响性能变差的问题,提出交流异步电机矢量控制系统的模糊-PI复合控制方式,通过对交流异步电机的数学模型分析设计出模糊PI控制器。利用MATLAB/ SIMULINK仿真平台构造出一个交流电机矢量控制系统的仿真模型,最后给出并分析仿真结果。仿真结果表明,该系统具有良好的适应性和鲁棒性。

模糊PI控制;矢量控制;异步电机

交流异步电机是一个高阶、多变量、强耦合的非线性系统,常规控制中一般采用参数重构和坐标变换方法来实现对交流异步电机定子电流励磁分量和转矩分量的解耦控制,这种控制方法的最大问题在于电机的运行状态容易受到电机参数变化的影响。此外,常规PI速度调节器的参数依赖于电机的精确数学模型,因此调速系统性能受到电机参数变化和环境变量的影响[1]。模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的一种计算机数字控制。模糊控制也是一种智能控制,而且已成为目前实现智能控制的一种重要而有效的形式,具体来说,它是“采用模糊集合理论和模糊逻辑,并同传统的控制理论相结合,模拟人的思维方式,对难以建立数学模型的对象实施的一种控制方法”。具有响应速度快、超调量小等优点。

Matlab是一种面向工程计算的高级语言,它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案[2]。Simulink是MATLAB最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境,使用它可以大大提高系统仿真的效率和可靠性。在Simulink环境下,利用模糊控制理论不依赖于被控对象精确数学模型的特点、构建模糊PI复合控制器的模型,通过调整并设计加入控制因子,以增加系统鲁棒性,使电机获得稳定的输出。

1 矢量控制系统中电机数学模型

交流异步电动机的动态数学模型是一个高阶、非线性、强耦合的系统,要实现高动态调速性能的控制方案,必须基于异步电机的动态模型[3],然而动态模型控制非常复杂,而如果将其简化成单变量线性系统进行控制,又达不到理想的性能。随着数字控制技术、电力电子器件的发展,20世纪70年代提出的矢量控制方案已得到了广泛的应用。在矢量控制中,一般常采用两相静止坐标d-q轴下的电机模型。异步电机在d-q轴下的数学模型如下,其中定子电流和转子磁链为状态变量。

其中,R1为定子电阻,R2为转子电阻,L1为定子自感,L2为转子自感,M为互感,ωr为转子角速度,ω1为电源角频率,式中。电机的运动方程式式中P是磁极对数,J是转动惯量,TL是负载转矩。

常规的矢量控制方法一般是比较输入转速指令和反馈的电机实际转速,用其偏差作为控制量,经过PI调节器后得到转矩电流指令,再由矢量控制算法得到定子电压指令值,最后通过逆变器实现对电机输入电流的幅值和频率的调节[4]。这种常规的控制方法使得电机的运行状态容易受到电机参数变化的影响。基于此,很多人提出了理想的矢量控制(即非干涉控制)方法,而该方法对电机参数变化也很敏感,特别是对转子时间常数L2/R2的变化敏感,且在启动过程中系统转速相应较慢,因此设计系统时在非干涉控制方法中加入了修正因子,以克服上述缺点。

2 模糊PI控制器的设计

在异步电动矢量控制中,电机的各参数通常由PI控制器实现,由于采用工程设计方法得到的PI控制器参数Kp和Ki是固定的,无法适应异步电机运行的全过程设计的系统中采用了具有修正因子的模糊控制器,它具有快速的响应和较小的超调,且具有很强的鲁棒性,并能够克服非线性因素的影响,可利用模糊推理实现实时调整PI参数,使PI控制器适应异步电机运行过程的变化,获得良好的控制性能。

模糊PI控制器结构如图1所示,以转速偏差E和转速偏差误差的变化率EC作为模糊控制器的输入变量,输出变量为转矩电流指令。

图1 模糊PI控制器结构图

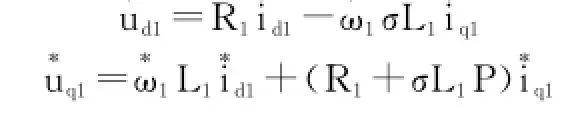
把每个变量的论域分为七个模糊集合:负大(NL)在-3附近,即NL=-3;负中(NM)在-2附近,即NM=-2;负小(NS)在-1附近,即NS=-1;零(ZE)在零附近,即ZE=0;正小(PS)在1附近, 即PS=1;正中(PM)在2附近,即PM=2;正大(PL)在3附近,即PL=3;选取mamdani的逻辑推理方法,各语言变量的隶属度函数均采用均匀分布的三角函数。隶属度函数如图2所示。

加入修正因子α的输入输出关系为:Iq=α*E +(1-α)*EC,其中α为修正因子,取值范围在0 和1之间。修正因子α的取值大小就表示对偏差E和偏差变化率EC所加的权重。由于电机启动时转速易发生震荡,应取E的权重略大于EC的权重,现取a=0.7.输出转矩电流指令值Iq按前式计算,并对结果进行圆整,得到如下表1所示的模糊控制规则表。

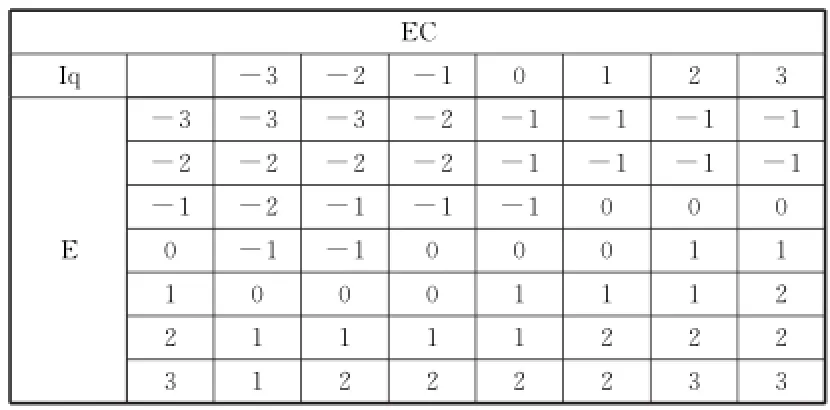
表1 模糊控制规则

把表1中对应的模糊规则输入到模糊控制器,得到了仿真中用到的模糊PI控制器,从中可以观察到控制器输入输出关系曲面射,如图3所示。

图2 隶属度函数曲线

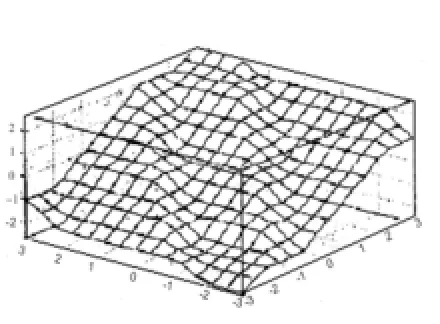
图3 输入输出关系曲面

3 模糊PI复合控制系统仿真

设计的模糊PI复合控制系统由控制器和异步电机两大主要部分组成,控制器由模糊控制器、PI控制器、非干涉矢量控制算法、空间矢量变换组成。由于该系统用模糊PI复合控制代替了常规矢量控制系统中的PI控制器,为了突出复合控制器的设计,不妨在仿真时省去空间矢量变换和PWM逆变器部分。异步电机则直接采用d-q轴下的电机模型。模糊PI复合控制系统的SIMULINK仿真模型如图4所示。

图4 模糊PI复合控制系统仿真模型

图中K1、K2为量化因子,分别把E和EC量化到离散论域[-3,3];K3为比例因子,把模糊控制器的输出Iq转化为转矩电流指令值,为了防止输入变量的语言值超出所设定的模糊规则之外,可加入上下限限制E和EC在论域[-3,3]内。

在仿真调试时可以适当调整K1、K2和K3的取值以取得最佳系统性能。K4和K5分别为pi/30和30/pi,用于转速单位r/min和rad/s之间的转换。

如果只采用模糊控制器进行控制,系统存在稳态误差。为了消除稳态误差,可用模糊控制和PI控制组成并联结构,当转速偏差较大时进行模糊控制,当转速偏差较小时把PI控制器的输出叠加到模糊控制器的输出上,利用积分器的作用来消除稳态误差。图中选择开关用于决策是否投入使用PI控制器,如当转速偏差小于10rad/s是选择PI控制器,否则选择模糊PI控制。

4 仿真结果

仿真中用到的异步电机的参数如下:R=0. 662Ω,R2=0.645Ω,L1=0.086H,L2=0.086H,M =0.086 H,J=0.0168kgm2,i*q1=3.2A,P=2.可得到如下图的电机转速动态特性。

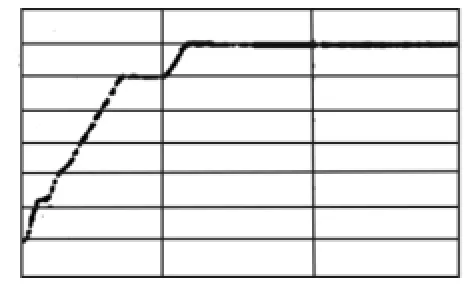
图5 电机转速动态特性

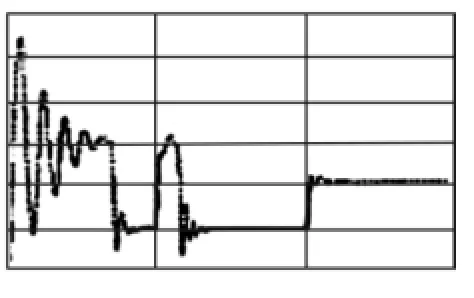
图6 转矩动态特性

给定转速指令初始值为1000r/min,在0.5秒时突变为1200r/min,负载转矩的初始值为5N·m, 在1秒时突变为10N·m,图5中,电机转速能迅速的跟踪转速指令值。启动后,大约在0.35秒时转速达到1000r/min,转速指令突变时,在0.1秒内转速增加至1200r/min。启动过程中电机的转速波动很小,没有稳态误差和超调。负载突变时,转速的瞬态变化量非常小,转速基本上没有波动。

由图6中的电机的转矩仿真曲线看出,电机负载启动时虽然输出有一定的脉动,但其大体的变化趋势还是比较理想的,能够在电机启动时输出较大的电磁转矩。转速指令值突变时,输出转矩能够迅速增加,使电机转速上升,转速跟踪到指令值后,输出转矩又迅速返回到与负载转矩相平衡的状态;外加负载突变时,输出转矩也迅速增加,很快平衡了突加的负载,维持转速基本不变。

5 结论

利用SIMULINK建立的模糊PI异步电机复合控制,简单快捷,直观且灵活,由于在模糊控制器中设计了修正因子使得电机输出转矩能迅速跟随负载转矩,对于负载突变能予以快速平衡,为实际中控制异步电机的转速给出了较成功的模型。模糊PI复合控制方式对电机转速的稳定性、精确性和高效性能进行有效的控制,对于开发和研究调速系统有很好的借鉴意义。

[1]陈伯时,等.交流调速系统[M].北京:机械工业出版社,2005:68-135.

[2]洪乃刚.电力电子、电机控制系统的建模与仿真[M].北京:机械工业出版社,2010:5-40.

[3]毛晓英.基于MATLAB/SIMULINK的异步电动机矢量控制调速系统仿真[J].东北电力技术,2004,(1):14-16.

[4]刘俊,庄圣贤.三相异步电机矢量控制的研究[J].电气开关,2010,(2):26-30.

TM343

A

1672-9846(2013)02-0075-03

2013-04-16

湖北省高等学校青年教师下企业行动计划项目(编号:XD20100921)。

周凌华(1975-),女,湖南永州人,武汉交通职业学院机电工程学院讲师,工程师,主要从事电气自动化技术研究。