基于航线对象的五边进近调配程序模型研究

赵嶷飞，刘然，王红勇

（中国民航大学国家空管运行安全技术重点实验室，天津300300）

基于航线对象的五边进近调配程序模型研究

赵嶷飞，刘然，王红勇

（中国民航大学国家空管运行安全技术重点实验室，天津300300）

针对进近管制飞行密集、潜在冲突多、调配难度大的特点，提出一种智能化的调配程序研究方法。将五边调配程序分解为基本的飞行程序，并引入航线对象的概念，结合五边进近飞行特点建立调配程序的参数模型。通过模型计算得到关键位置点及飞行控制参数信息，同时生成飞行路径，综合全部信息即得到完整的调配方案，能够为实际管制工作提供参考和服务。计算机仿真结果证明了理论方法的可行性。

空中交通管制；五边进近；调配；航线对象；飞行参数

随着中国航空运输量的日益增长，进近管制区已成为飞行事故和事故征候的多发地带。进近管制的特点是飞行密度高、潜在冲突多、调配难度大。雷达管制下的调配方法是解决终端区内飞行冲突的手段依据。但繁忙的空域交通流量已超过管制员的能力范围，需要引入自动化的支持工具。

管制调配方法实质上是机动的飞行程序。飞行程序是航空器飞行时使用的飞行路线[1]，由基本参数确定。飞行程序的参数模型已被用于空中交通仿真和4D航迹预测，还未应用到管制方法的研究当中。

本文旨在将调配过程分解为基本的飞行程序，并基于航线对象的概念，结合五边进近飞行特点建立调配程序的参数模型，通过模型计算可以得到飞行控制参数信息，并将信息点拟合成飞行路径生成完整的决策方案。经过对算例的仿真验证，表明对调配方法的过程控制研究是可行的，能够为实际管制工作提供更好的参考和帮助。

1 五边进近调配

通常五边进近航线分为以下部分：三边（downwind）、三转弯、四边（base）、四转弯、五边（final）。如图1所示。

为便于计算分析，并考虑实际的飞行过程，将五边进近航线概括为表1所示的飞行阶段。

雷达管制的主要目的是为了提高空域的利用率，引导航空器按最优最佳的路线飞行[2]。进近雷达管制调配飞行冲突的主要方法是对航空器进行引导，指挥其按管制员拟定路线机动飞行。整个飞行过程实际上是灵活机动的飞行程序，即调配程序。本文研究重点在于调配程序参数模型的建立和求解。

图1 五边进近航线定义Fig.1Definition of final approach

表1 五边进近飞行阶段Tab.1Final approach flight phase

2 基于航线对象的基本飞行程序

2.1 五边进近基本飞行模型

基于五边进近航线飞行特点，本文提出了三边（downwind）至五边（final）航段飞行的基本模型如下：

1）等表速水平直线飞行（NC）：主要五边（final）航段上的飞行。

2）减速水平直线飞行（SC）：该模型为速度改变的机动飞行。

3）等表速转弯下降（AC）：该模型是高度和方向改变的机动飞行，水平方向做等速水平转弯。

4）等表速水平转弯（HC）：在等高度、等速度的情况下改变方向的机动飞行。

5）减速直线下降（SD）：该模型在水平方向上做减速运动。

2.2 基于航线对象的基本飞行模型

将现有的STAR（standard terminal arrival route）和SID（standard instrument departure）等飞行程序简化成由几个位置点和若干参数组成的标准程序，即航线对象[3]（path objects，简称PO）。

由于航线对象是一段存储在计算机中的指令序列，用于构造航空器在航路中飞行，或者终端区内起飞/下降着陆时使用的飞行路线。它是由若干位置点和控制参数组成的指令序列，用来描述航空器在飞行中使用的等待程序、复飞程序、STAR、SID等飞行程序。位置点使用三维坐标[x，y，z]表示，x和y表示平面地理坐标即经度和纬度，z表示高度坐标，控制参数可以包括：时间参数、距离参数、高度参数、角度参数以及基本飞行模型参数等。根据各飞行程序与飞行阶段之间的关系，飞行程序可由基本飞行模型组合而成，并结合航线对象思想，将飞行程序实现计算机指令化。

2.3 由航线对象的飞行程序

常用的飞行程序包括直线航段、转弯等。本文将使用航线对象的概念分别进行描述。

2.3.1 直线航段

直线航段是结构最简单的飞行程序，如图2所示，直线航段一般发生在减速平飞模型和匀速平飞模型，直线航段的一种PO表达方式：[L，p1，p2，i]。其中，L是这个PO的名称，两个位置点p1、p2分别为起点和终点，i为基本飞行模型，这里i可以为NC、SC、SD等，其坐标为p1=[x1，y1，z1]，p2=[x2，y2，z2]。该直线航段的距离为d，用下列公式计算

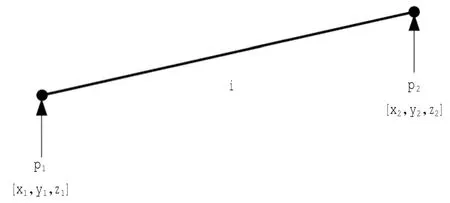
图2 直线航段Fig.2Straight line leg

2.3.2 转弯

1）直线转弯

图3显示直线转弯程序，它的一种PO定义方式：[T，p1，α，d1，β，d2，i]，由1个位置点p1、2个航向参数α、β和2个距离参数d1、d2组成，其中i为HC模型，p3表示中间点，其含义为飞机从起点p1沿航向α飞行距离d1，然后沿航向β飞行距离d2。

2）曲线转弯

图4显示曲线转弯程序，其PO定义为：[T，p1，p2，p3，r，i]。由3个位置点和一个距离参数r组成，其含义为：从p1开始飞行，沿着p1到半径为r圆的切线飞到切点p3，然后沿着该圆周飞行至p2点，最后沿着经过p2点的圆切线继续飞行。

图3 转弯程序一Fig.3The first of turn procedure

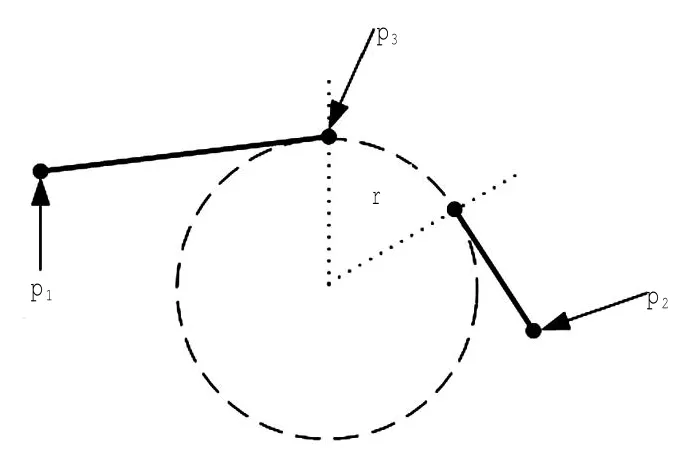
图4 转弯程序二Fig.4The second of turn procedure

3 飞行程序基本参数计算

通过前面的理论分析，基于航线对象的思想建立了直线航段和飞行转弯的控制参数程序。五边调配程序可以以直线和转弯程序为基础组合应用。从二维平面来看，其水平航迹由一系列直线飞行段和圆弧飞行段组合而成[4]。

结合已建立的五边航段基本飞行模型，下面给出直线飞行程序和转弯飞行程序的参数计算模型。

3.1 直线程序

直线程序包括等速水平直线飞行、减速水平直线飞行、减速直线下降等飞行阶段。

3.1.1 水平直线飞行

水平直线飞行如图5所示。

1）匀速直线运动

已知起始点p1位置坐标（x1，y1，z1），速度v，航向ψ，水平飞行距离Δs。结束点p2位置坐标（x2，y2，z2）和飞行时间Δt可由式（1）、式（2）解得

图5 水平直线飞行Fig.5Straight and level flight

其中：θ=180°±ψ。

2）减速水平运动

已知起始点p1位置坐标（x1，y1，z1），速度v1，水平减速飞行至p2（x2，y2，z2），速度v2，飞行距离为Δs。由下式计算飞行时间Δt和结束点p2位置

p2位置坐标计算同式（1）。

3.1.2 减速直线下降

减速直线下降如图6所示。

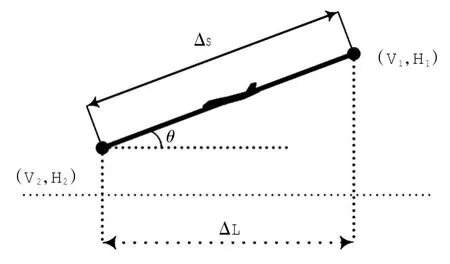
图6 减速直线下降Fig.6Deceleration descend

减速下降存在高度变化量ΔH=H1-H2，应用三维运动方程计算结束点位置坐标、速度和飞行时间Δt。

根据能量方程计算结束点速度V2

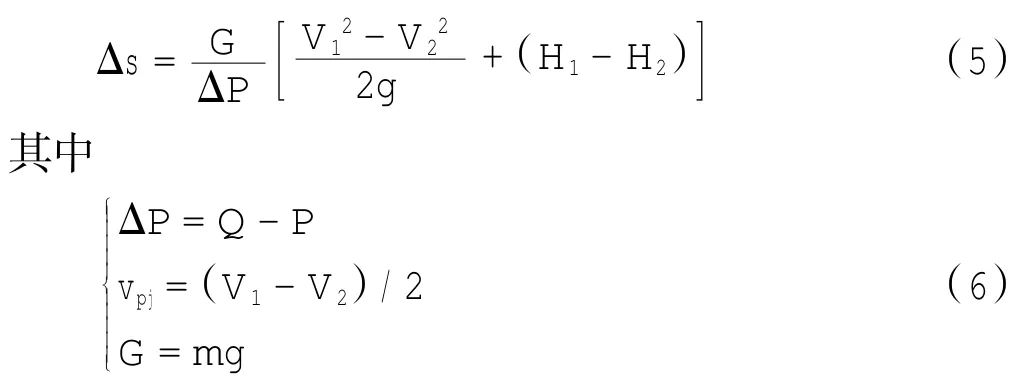
其中：G为飞机重量；m为飞机质量；g为重力加速度；V1、V2、H1、H2分别为起点和终点时航空器的速度和高度；发动机推力P和气动阻力Q可根据高度、速度和M数的平均值，按发动机工作状态和相应构型下的气动特性来确定[5]。

结束点的坐标计算公式为

3.2 转弯模型

五边飞行转弯一般为等速水平转弯，如图7所示，由管制员指定转弯角度，航空器只需从当前航向内切转弯到目标航向即可完成转弯，飞行内切转弯指定半径的转弯圆弧与两个直线航段均相切[6-7]。

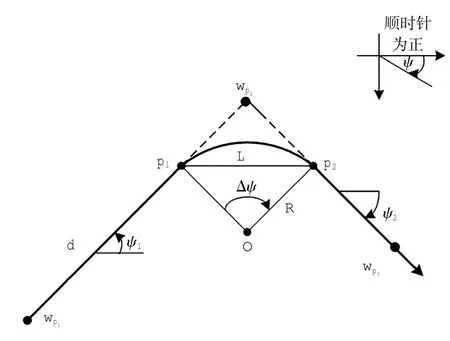
图7 内切转弯计算方法Fig.7Method of turn calculation

p1和p2是图中飞行航段的起始和结束转弯点。航空器以ψ1航向往航路p2点飞行，从p1点开始一个半径为R的圆弧转弯，直到切到目标航向ψ2的p2点结束。由已知的p1坐标（x1，y1，z1）、速度v、转弯坡度、转弯率r=3°/s、转弯角度Δψ，确定转弯飞行时间Δt和转弯半径R，g为重力加速度。

转弯问题可以描述成：已知初始条件[p1（x1，y1，z1），R，ψ1，ψ2]，求转弯结束点p2（x2，y2，z2），计算公式为

4 算例验证

本文前面内容分析了五边进近管制调配方法的飞行程序模型。通过模型的参数计算可以得到调配引导飞行路径的位置点位置及飞行参数，综合这些过程信息便可获得完整的调配程序。

4.1 算例分析

下面通过计算分析五边进近管制中的延长三边飞行调配方法，验证理论方法的可行性。

由图8过程所示，航空器A即将转入五边（final）飞行，若航空器B由三边飞行终点1经四边（base）转入五边，将与A机在五边上的间隔小于安全范围，发生危险进近[8]。管制员采取延长三边的策略，引导B机延长三边飞行至结束点2，经三转弯至四边起始点3，再经四边飞行至结束点4，由四转弯至五边起始点5。整个飞行过程由三边、四边两个直线飞行航段和三、四转弯两个转弯程序构成。全过程的控制参数包含点2，3，4，5位置信息，航空器过各点时的速度，转弯飞行的转弯角度、半径以及各边航向等。

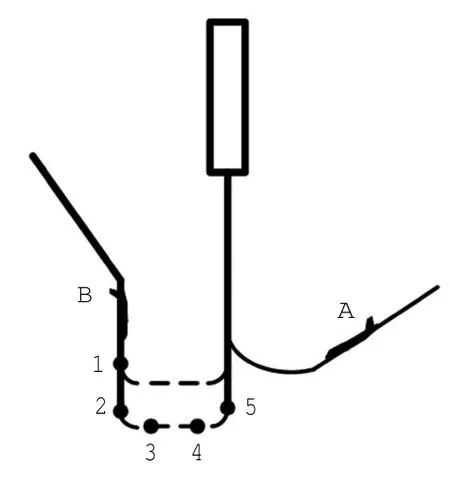
图8 延长三边调配程序Fig.8Deployment procedure of extended downwind leg

整个飞行过程是连续的，各位置点既是前一个航段的结束点同时也是下一个航段的起始点，这些点可互为起始状态参数。为得到可行性方案采取逆向推导计算位置点及相关参数值。即确定点5的位置坐标、飞行航向和速度，将其带入转弯模型，在确定转弯半径和指定转弯角度后根据模型计算得到四边飞行航向、速度以及点4位置坐标，转弯飞行时间，同理依次推导计算得到程序所需全部控制参数数据和各航段飞行距离和时间。

4.2 仿真计算

编写Matlab程序，输入已知状态参数进行计算，得到各飞行航段始末位置及控制参数值，输出运算结果即为完成的调配方案。

输入初始参数如图9所示，计算所得各航段始末位置坐标，各段速度及航向，转弯参数，各航段飞行时间将在命令窗口中输出显示。综合路径点及飞行参数生成飞行航迹如图10所示，位置点2、3、4、5二维地理坐标已在图10中标明，虚线段为延长三边飞行航段，2、3点间的弧线段为三转弯，3、4点间线段为四边，4、5点间弧线段为四转弯，5点为起点的水平线段为五边航段。

图9 输入初始参数Fig.9Initial parameter

图10 飞行路径图Fig.10Map of flight path

路径的连续性验证了飞行过程控制参数的相关性，表明本文的理论方法是可行的。

5 结语

本文根据过程控制的思想，将五边进近管制调配过程描述为以控制参数形式表示的飞行程序。基于航线对象理论，将调配程序分解为由若干段直线和转弯的基本飞行程序，并根据飞行阶段状态建立基本飞行程序模型，通过运动学方程计算控制参数得到过程位置点的位置信息及基本飞行数据。利用计算所得数据生成航迹即得到完整的调配程序，给管制员提供智能决策帮助，实现管制调配的自动化。

[1]戴福青.飞行程序设计[M].天津：天津科学技术出版社，2000.

[2]杨昌其，王庆春，邹国良.进近雷达管制方法浅析[J].空中交通管理，2003（5）：11-14.

[3]刘宏.基于航班对象的空中交通仿真模块设计的研究[D].天津：中国民航大学，2005.

[4]王超，郭九霞，沈志鹏.基于基本飞行模型的4D航迹预测方法[J].西南交通大学学报，2009，44（2）：295-300.

[5]李晓勇，张康，鲁素芬，等.民用运输机首飞起落航线仿真软件设计与应用[J].飞机设计，2008，28（6）：18-21.

[6]SLATTERY R，ZHAO Y.Trajectory synthesis for air traffic automation [J].Journal of Guidance，Controland Dynamics，1997，20（2）:232-238.

[7]BOLENDERM A，SLATER G L.Departure Trajectory Synthesis and the Intercept Problem[C]//AIAA Guidance Navigation and Control Conference.New Orleans:National Aeronautics and Space Administration，1997：444-454.

[8]肖德义.雷达管制条件下终端区航空器排序策略分析[J].空中交通管理，2008（3）：11-13.

（责任编辑：杨媛媛）

Analysis of final approach deployment procedures based on path objects

ZHAO Yi-fei，LIU Ran，WANG Hong-yong
（National Key Laboratory for Air Traffic Management Operation Safe Technology，CAUC，Tianjin 300300，China）

For the fact that approach control is characterized by high flight-density,numerous potential conflicts and large deployment difficulty,an intelligent deployment procedure is proposed.To establish a parameter model, the final approach deployment procedure is divided into several basic flight procedures,combined with the concept of path objects and the features of final approach flight.By model calculating,we can collect information of the key location points as well as flight control parameters,and generate the flight path;all the data are integrated to form a complete deployment scheme,which can provide reference and service for the actual flight controlling practice.Feasibility of the theoretical method has been proved through simulation calculation.

air traffic control；final approach；deployment；path objects；flight parameter

V351

A

1674-5590（2013）03-0001-05

2012-05-04；

2012-08-10

国家科技支撑计划（2011BAH24B10）；国家自然科学基金项目（61039001）；中国民用航空局科技基金项目（MHRD200913）；中央高校基本科研业务费专项（ZXH2010C010，ZXH2009A004）

赵嶷飞（1971—），男，湖南常德人，教授，博士，研究方向为空中交通规划与管理.