基于改进的模糊C-Means航迹聚类方法研究

王超，王明明，王飞

（中国民航大学空中交通管理学院，天津300300）

基于改进的模糊C-Means航迹聚类方法研究

王超，王明明，王飞

（中国民航大学空中交通管理学院，天津300300）

为指导飞行程序的改善和发现管制员的指挥模式，在分析历史飞行航迹特征基础上，应用最小描绘长度（MDL）原理对航迹特征点进行划分，运用融合了遗传算法和模拟退火算法的改进的模糊C-Means算法对特征点进行聚类，通过最长公共子序列（LCS）算法得到航迹相似性矩阵，利用矩阵得到航迹簇，最后形成中心航迹，算例仿真验证了新算法的有效性。

航迹聚类；遗传模拟退火算法；模糊C-Means；最长公共子序列

空中交通流量的不断增长对目前基于雷达监视的管制指挥提出了严峻挑战，给管制员带来了持续排序引导、绕飞、备降等工作负荷。特别是在有些大流量终端区，管制员在指挥大流量航班排序时，为保证飞机的安全间隔而实施复杂的雷达引导，导致航班的飞行航迹偏离标准的进离场航线。大量事实说明有些终端区的进离场航线设计已不能适应变化的空中交通流量水平，因此，本文从历史航迹聚类的知识发现角度[1]出发，找出适应当前空中流量的飞行中心航迹，对于改善终端区进离场航线的组织规划具有较重要的意义。

航迹聚类分析是依据数据挖掘（data mining）中聚类分析的方法，通过引入相关学科的知识来不断改善聚类的效果。运动物体轨迹数据（如飞行航迹）包含着新的属性维（如位置、时间、速率和方向等），相应的聚类分析就需要采用新的方法。国内外主要有两大类方法：①Gaffney S.等人最早对移动对象轨道聚类进行的研究[2]，对一条物体轨迹作为一个整体来处理，注意到一条轨迹经过的路径很长很复杂，许多轨迹可能会有一小段相似而在整体上是不相似的。②JaeGil Lee，Jiawei Han[3]等人提出把一条轨迹分为一组短线段，然后聚类相似线段，这样可以发现局部相似线段，但又缺少了轨迹整体性。

本文在韩中华[4]等人对终端区航迹聚类研究的基础上进行改进，研究中的飞行航迹数据由大量离散的航迹点p=（X，Y，Z，V，Healing）组成，这些点都通过雷达扫描间隔中得到，有些点不是飞行高度、速度和方向显著变化的点，所以需要对这些航迹进行划分，找出特征点，然后应用模糊C-Means聚类算法对特征点进行聚类，但其不是全局的搜索聚类算法，所以本文加入了遗传算法的全局性和模拟退火算法的局部快速搜索性能，这样就能够准确快速的找出聚类中心点。然后用这些聚类中心点表示每一条航迹，通过最长公共子序列（LCS）找出相似航迹，最后对相似航迹簇进行聚类得到中心航迹，既保持了航迹的整体性又不失局部偏离特性。

1 航迹聚类模型

本文的聚类模型是基于航迹特征点的聚类，先结合信息论中的MDL（minimum description length）准则对航迹进行划分，然后应用模糊C-Means算法对得到的特征点进行聚类。

1.1 基于MDL的特征点划分

飞行航迹的特征点[5]包括航路点、速度转换点、高度转换点、航向转换点、速度限制点、高度限制点、距离限制点、转弯起始点、转弯结束点等，代表了整条航迹的主要信息。为了提高聚类速度，需要找出飞行航迹的特征点。如图1所示，用Pc1、Pc2来表示P1、P2、P3、P4。

图1 特征点的描述Fig.1Description of character

本文从飞行轨迹TRi=P1P2…Pleni中选择出一组特征点Pc1Pc2…Pcpari（1≤c1＜c2＜…＜ck≤leni），由于研究的目的是终端区历史航迹的中心航迹，所以这里忽略速度的影响。目标函数是min（L（H）+L（D/H）），近似轨迹划分算法主要是将局部最优解视为全局最优解，思想如下[3]：假设MDLpar（pi+pj）表示仅当pi和pj之间一段轨迹的MDL代价为L（H）+L（D/H）；MDLnopar（pi+pj）表示当pi和pj不是特征点且pi和pj之间没有特征点时的MDL代价为L（H），其中L（D/H）为0，局部最优解就是满足MDLpar（pi+pk）≤MDLnopar（pi+pk）的最长轨迹划分pipj，其中i＜k≤j。如果前者比后者小，那么选择pk作为特征点将比不选择它作为特征点的MDL代价小，同时算法尽可能的增加轨迹划分的长度以达到简明性。其中

式中：len（pcjpcj+1）是线段pcjpcj+1的欧式长度，d⊥（pcjpcj+1，pkpk+1）是线段之间的垂直距离，dθ（pcjpcj+1，pkpk+1）是线段之间的角度距离，如图2所示。

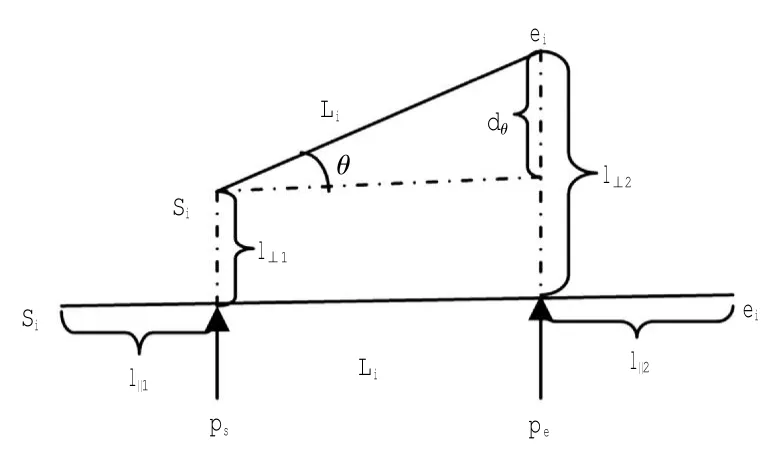
图2 空间线段之间的距离Fig.2Distance between space segment

其中

1.2 模糊C-Means聚类算法

模糊C-Means（FCM）聚类算法[6]是一种基于目标函数的聚类算法，其形式为

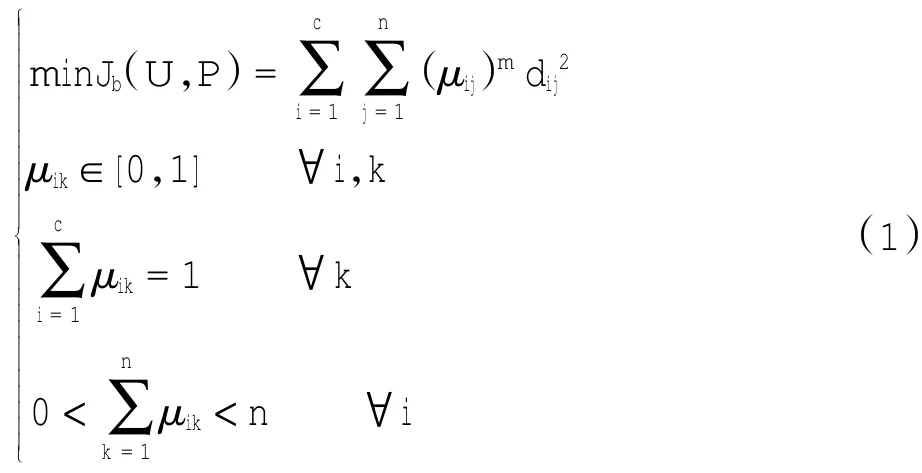
式中：i为类别下标（i=1，2，…，c），代表航迹聚类中心点；k为元素下标（j=1，2，…，n），代表历史航迹的特征点；n为元素总数；U为隶属度矩阵，U=（uik），uik表示第k元素隶属于第i类的隶属度；dik2=（xk-vi）T（xk-vi）表示距离。

用拉格朗日乘数法求解，得

式中：μik=1，djk=0且i=j。

同理，可得类中心为

用式（2）和式（3）反复修改数据隶属度和聚类中心，当算法收敛时，理论上就得到了各类的聚类中心以及各个样本对于各类的隶属度，从而完成了模糊聚类划分。尽管模糊C-Means聚类算法有很高的搜索速度，但它是一个局部搜索算法，如果初值选择不当，它就会收敛到局部极小点。

2 航迹特征点聚类模型的改进

模糊C-Means聚类算法[7-9]是一种局部搜索聚类算法，应用遗传算法的优势使它达到全局最优，并且为了提高算法局部搜索速度，还结合了模拟退火算法的优势，这样既保持了航迹的整体性又不失局部偏离特性。

2.1 遗传算法实现

1）编码方式

本文采用的是二进制的编码方式，待优化的参数是c个初始聚类中心，这里使用二进制编码，每条染色体有c个聚类中心组成，对于m维的样本向量，待优化的变量数为c×m，每个变量使用k位二进制编码，则染色体为长度是c×m×k的二进制码串。

2）适应度函数

3）选择算子

求出群体中每一代每个个体的适应值fi，然后按轮盘赌的比例选择法进行选择。

4）交叉算子

交叉算子采用简单的单子交叉的方法进行进化。

5）变异算子

以一定概率产生变异基因数，用随机方法选出发生变异的基因。如果所选的基因的编码为1，则变为0；反之则变为1。

2.2 改进的模糊C-均值聚类

步骤1对参数进行设置：种群个体大小sizepop，最大进化次数max gen，交叉概率Pc，变异概率Pm，退火初始温度T0，温度冷却系数k，终止温度Tend。

步骤2随机初始化c个聚类中心，并生成初始种群chrom，对每个聚类中心用式（2）计算各样本的隶属度，并求得每个个体的适应度值fi，其中i=1，2，…，sizepop。

步骤3设循环计数变量gen=0。

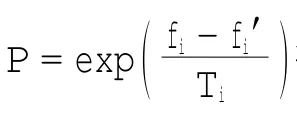
步骤5若gen＜max gen，则gen=gen+1，转至步骤4；否则，转至步骤6。

步骤6若Ti＜Tend，则算法成功结束，返回全局最优解；否则，执行降温操作Ti+1=kTi，转至步骤3。

3 航迹聚类

通过上述对航迹特征点聚类之后，每条航迹的特征点都被划分到不同的点簇。可用这些点簇的中心点来表示航迹。假如代表两条航迹的中心点都相同，则认为这两条航迹的相似性为100％。实际情况则是大多数航迹对只有一部分中心点相同。所以可以用相似性度量值来表示两条航迹之间的相似性大小。若两条航迹的相似性度量值超过一定阈值，则认为这两条航迹相似。

已知两条航迹：TRp可以用p个中心点来表示，TRq由q个中心点来表示。如图3所示，假设代表两条航迹的相同中心点为p1，p2，…，pi，…，ps共s个，则两条航迹之间相似性可表示为式（4），dij的值越大，TRp和TRq的相似性越高

图3 两条航迹的中心点Fig.3Central pionts of two tracks

基于式（4）可以得到n条航迹之间的相似性矩阵[10]D，如式（5），dij=dji，对于∀i=j，dij=1

利用航迹之间的相似性矩阵（5）对历史航迹分类，然后对每个历史航迹簇的航迹特征点进行聚类，最后得到中心航迹。

4 算例仿真

飞行航迹TP=（p1，p2，…，pn）是由有限个航迹点构成，案例选择某机场28R号跑道超过400个航迹点p=（X，Y，Z，V，Healing）的114条历史航迹（59 161个航迹点），然后进行划分和聚类分析。

4.1 飞行航迹特征点划分

应用MDL准则对飞行航迹进行划分得到航迹特征点，如图4～图6的流程所示。

图4827 条历史航迹Fig.4827 Historical trajectories

图5114 条历史航迹Fig.5114 Historical trajectories

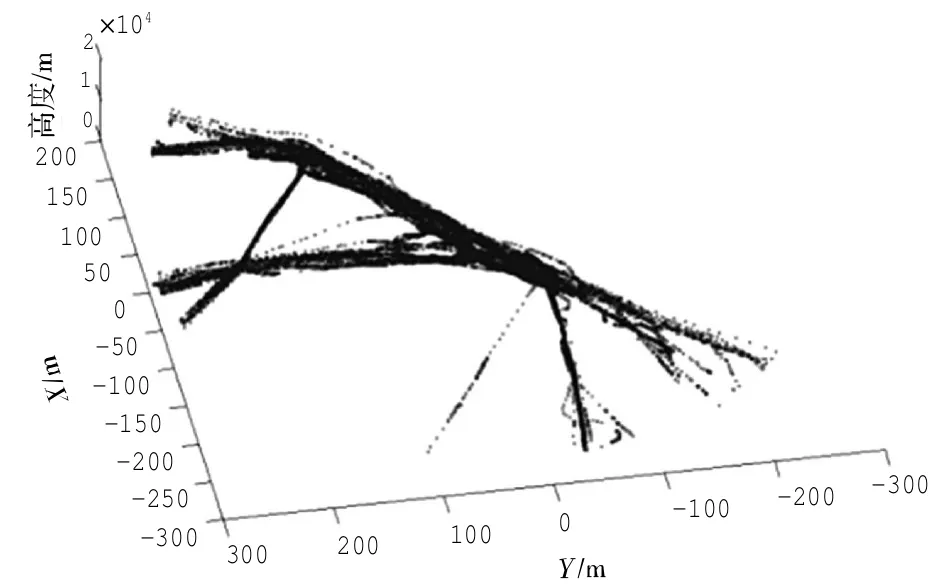
图6114 条航迹的特征点Fig.6Characters of 114 trajectories

从图6可以看出，通过MDL准则对114条航迹59 161个航迹点进行划分后得到16 307个特征点，然后按照下一步对这些特征点进行聚类。

4.2 航迹特征点的聚类

本文根据数据量的大小和算法的特性进行了参数的设定，因为FCM算法的目标函数就是用拉格朗日乘数法求解的，所以具有局部最优的特性，因此本文设置聚类中心的数目可以大一些，这样经过遗传算法的全局搜索性更能描绘出飞行航迹的真实状况，经过试验取60个聚类中心可以很好的代表航迹的轨迹特征。

模糊C均值聚类参数，m=3，幂指数；nmax=20，最大迭代次数；Jend=1.0×10-6目标函数的终止容限；cn=60，代表聚类数，也就是飞行航迹的聚类中心数。

模拟退火算法参数，q=0.8，冷却系数；T0=100，初始温度；Tend=1，终止温度。

遗传算法参数，sizepop=10，个体数目；max gen= 100，最大遗传代数；preci=10，变量的二进制位数；pc=0.7，交叉概率；pm=0.01，变异概率。

然后对16 307个特征点进行聚类得到如图7所示的60个聚类中心，可以看出60个聚类中心很好地代表了航迹的轨迹特征。

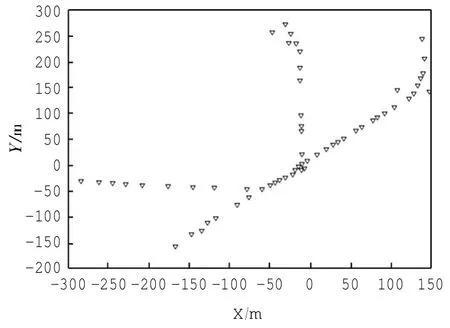
图7 聚类得到的特征点Fig.7Characteristic points by clustering

聚类的效果用式（1）中的Jb值来衡量，通过图8可以看到GASAFCM算法聚类每次仿真遗传100代Jb逐渐减小并且趋于稳定，单独FCM聚类有很大的不稳定性且Jb值较大。

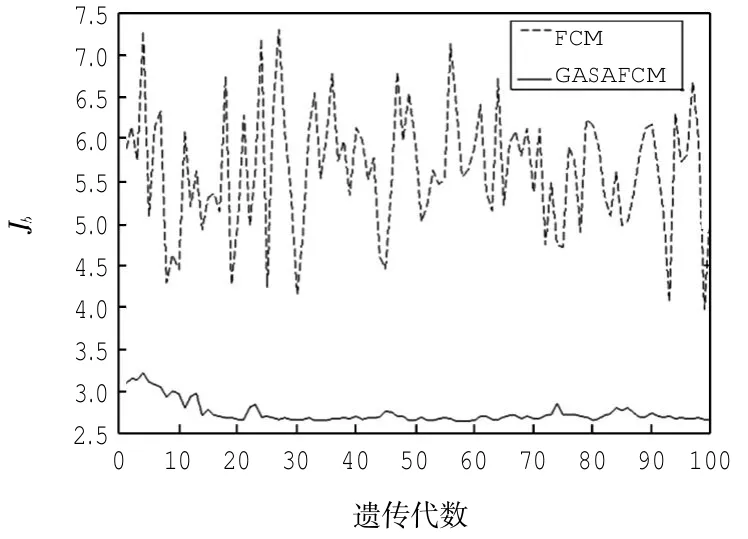
图8 基于Jb值的性能比较分析Fig.8Jbvalue-based on performance analysis

4.3 历史航迹的聚类

通过上一步可以得到60个聚类中心，然后用聚类中心表示每一条航迹，因为每条航迹可能有不同的聚类中心点表示，所以用LCS对航迹相似处理，得到航迹的相似性矩阵，运用相似性矩阵对航迹归类得到航迹簇，如图9所示。

图9 航迹簇Fig.9Trajectory clusters

4.4 中心航迹的聚类生成

对每个历史航迹簇的航迹特征点进行聚类，最后得到中心航迹，如图10所示。

图10 聚类出的中心航线Fig.10Center routes by clustering

5 结语

本文把遗传算法和模拟退火算法应用于飞行航迹的聚类当中，仿真实验表明其有很强的收敛性和稳定性，有效改善了单独FCM聚类的局部性和不确定性，另外还把信息论中的MDL原理应用到航迹特征点的划分当中，对一些不是特征点的航迹点进行了删减，运用到航迹聚类中得到很好地真实效果，同时还运用到最长公共子序列（LCS）算法来找出相似航迹，有效的避免了部分异常航迹的影响。通过整体的仿真实验表明这种方法有很强的直观性和真实性，但本文只是对FCM算法进行了改进并做了比较，没有与其它轨迹算法进行精确对比，在以后的研究中会继续改进此算法，并且把此算法运用到实际的终端区航线组织当中。

[1]HAN JIAWEI，KAMBE MICHELINE，范明，孟小峰，译.数据挖掘概念与技术[M].北京：机械工业出版社，2011：251-303.

[2]GAFFNEY S，SMYTH P.Trajectory Clustering with Mixtures of Regression Models[C].1999：63-72

[3]LEE JAEGIL，HAN JIAWEI，WANG KYUYONG.Trajectory Clustering：A Partition and Group Framework[C]//The 5th ACM SIGKDD International Conference on Knowledge and Data Mining，SanDiego，California，USA：2007，593-604.

[4]韩中华.终端区航迹聚类方法研究与应用[D].天津：中国民航大学，2010.

[5]王超，郭九霞，沈志鹏.基于基本飞行模型的4D航迹预测方法[J].西安交通大学学报，2009，44（2）：296-300.

[6]廖琴，郝志峰，陈志宏.数据挖掘与数学建模[M].北京：国防工业出版社，2010.

[7]侯慧芳，刘素华.一种改进的基于遗传算法的模糊C-均值计算[J].计算机工程，2005，31（17）：152-154.

[8]百莉媛，胡声艳，刘素华.一种基于模拟退火和遗传算法的模糊聚类算法[J].计算机工程与应用，2005（9）：36，56-57.

[9]张维，潘福铮.一种基于遗传算法的模糊聚类[J].湖北大学自然科学报，2002，24（2）：101-104.

[10]FRANK REHM.Clustering of Flight Tracks[C].AIAA2010-3412，2010 （20-22）.

（责任编辑：党亚茹）

Trajectory clustering method research based on improved Fuzzy C-Means

WANG Chao，WANG Ming-ming，WANG Fei
（College of Air Traffic Management，CAUC，Tianjin 300300，China）

In order to guide the improvement of flight procedures and find the command mode of the controller，this paper firstly analyzes the historical flight path，and categorize the characters by the minimum description length （MDL）theory，then clusters the characters using of the improved Fuzzy C-Means（FCM）method combined with the GA and SA，and receives the trajectory similarity matrix by the longest common subsequence（LCS），lastly generates the mean routs through the trajectory clusters.The simulation tests show that this new method is quite effective.

trajectory clustering；GASA algorithm；Fuzzy C-Means；longest common subsequence

V355

A

1674-5590（2013）03-0014-05

2012-07-04；

2012-08-28

国家科技支撑计划项目（2011BAH24B08）；中国民航大学研究生科技创新基金（YJSCX12-03）；中央高校基本科研业务费专项（ZXB2011A002）

王超（1971—），男，天津人，副教授，博士，研究方向为交通信息工程与控制，交通运输规划与管理.