电调谐式微带线滤波器的设计

任镍，张泽宇

（武汉船用电力推进装置研究所，武汉 430064）

0 引言

随着高速信号处理技术的发展，滤波器作为最基本的信号处理元件之一在各种控制系统中起着非常重要的作用。电调谐滤波器由于其中心频率可变、调谐方式灵活、构成方式多样等优点受到越来越多的关注，本文在电调谐滤波器原理的基础上[1]，研究了微带线外部耦合系数及级间耦合系数对电调谐式滤波器的影响，并基于提取参数法设计出了一种调谐范围宽、插损小的电调谐滤波器。

1 抽头式电调谐滤波器设计

本文基于滤波器设计的提取参数法[2]，它适用于各种不同的耦合滤波器物理结构。滤波器等效电路如下图1、图2所示。

由图1、图2可知，假定各谐振器的谐振频率ω，谐振器间耦合系数Mij，影响滤波器响应特性的主要参数就是：输入输出端口阻抗RL和RC。结合等效模型，抽头式梳状线滤波器端口阻抗RL和RC的大小取决于抽头线的位置，谐振频率ω取决于加载电容的大小，级间耦合系数Mij则取决于耦合微带线的线间距。

图1 n阶耦合谐振器的等效电路

图2 n阶耦合谐振器的双端口等效图

可以利用耦合结构设计法[4]来确定梳状线滤波器的物理尺寸参数。梳状线滤波器设计参数如下[5]。设定滤波器相对带宽值FBW为4%，低通原型的归一化值根据性能指标设定为g0=1、g1=0.8430、g2=0.6220、g3=0.6220。

那么滤波器外部品质因数：

耦合系数：

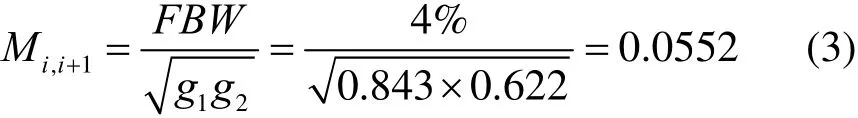
其中，i为滤波器的级数，Qe1和Qen为输入输出谐振器的外部品质因数，Mi,i+1为相邻谐振器间的耦合系数。

2 设计仿真

2.1 外部耦合系数和级间耦合系数的仿真

Ansoft HFSS是一种基于有限元方法的三维结构电磁场仿真软件，具备任意三维无源结构的全波电磁场分析求解能力以及强大的数据处理能力。本文在Ansoft HFSS中建立梳状线滤波器单端口三维模型和梳状线滤波器级间耦合三维模型，如图3和4所示。

图3 梳状线滤波器单端口三维模型

通过仿真计算，可以得出外部耦合系数与抽头对地距离的关系曲线，从而确定抽头对地距离为3.3 mm，通过级间耦合系数与微带线间距关系曲线从而确定微带线间距3.4 mm。

2.2 滤波器整体电路联合仿真

本文通过在 Agilent公司开发的 ADS（Advanced Design System）软件仿真版图和电路联合模型，抽头线梳状线滤波器模型如图5所示。

图4 梳状线滤波器级间耦合三维模型

图5 梳状线滤波器模型

再对其进行仿真优化后，得出了梳状线滤波器的参数曲线，如图6所示。

图6 入实际模型后的梳状线滤波器的仿真曲线

结合图6可得，电调谐滤波器的频率调谐范围为0.997~1.503 GHz，符合本文所预期的频段；插入损耗最大为4.554 dB，符合IL<5 dB的要求；相对带宽为4.1%~4.2%，略大于4%；端口驻波比<2；带外抑制>25 dB，满足项目设计的需要。

需要注意的几点是，滤波器的插损随频率的变化而变化，主要是由于等效串联电阻的影响。滤波器的低频端回波损耗特性并不是很好，这是由于在设计时所需用的是中心频率为1.25 GHz的带通滤波器，因此谐振器的长度和抽头对地距离以及耦合间距都是固定不变的 ，而抽头位置决定外部耦合，因此在低频端呈现过耦合状态，在高频端呈现欠耦合状态。

3 结束语

通过提取参数法对滤波器模型进行了仿真设计，设计出了1~1.5 GHz 的电调谐梳状线滤波器。仿真结果显示此滤波器电调谐频率范围宽、结构简单体积小巧、插入损耗低。设计过程发现品质因数更高的等效串联电阻可以减小滤波器的插入损耗，改进电调谐微带线滤波器低频和高频下的驻波系数，同时通过改进等效串联电阻的偏置电路可以减小偏置电路对滤波器带宽的影响。

[1] 李晓陆. 短波频率管理技术[J]. 舰船电子技术,2003, (5), 53-55.

[2] Penalva G. T., Risueno G. L., Alonso J. I. A simple method to design wide-band electronically tunable combline filters[J]. IEEE Trans, 2002, (50): 172-177.

[3] Jia-Sheng Hong. Microstrip Filters for RF/Microwave Applications[J]. New York: John Wiley&Sons, 2001,(10): 12-15.

[4] Matthaei G. Comb-line band-pass filters of narrow or moderate bandwidth [J]. The Microwave Journa1,1993(1): 35-38.

[5] Thomas A. Dimensions of microstrip coupled lines and interdigital structures [J]. IEEE Transaction on Microwave Theory and Techniques, 1977: 405-410.