多学科设计优化方法在燃气轮机设计中的应用

杨子龙，王志强

（1．中国舰船研究院，北京 100192；2. 中国船舶重工集团公司第七O三研究所，哈尔滨150036）

0 引言

随着科学技术日新月异的发展，燃气轮机设计的要求日益提高，其复杂程度已远超乎常人想象。设计不仅需要大量的人力，而且还牵涉到数十门学科。传统设计方法需要不断往复于各相对独立的“学科孤岛”之间进行分析计算，设计人员工作量大，产品开发周期长。多学科设计优化(Multidisciplinary Design Optimization，MDO)方法极大的缩短了结构设计周期，降低了设计人员的工作强度，并保证了设计前后燃气轮机的各项指标得到提高。

目前，多学科设计优化是基于确定性条件的优化过程，没有考虑产品设计的不确定因素。由于没有考虑这种不确定性因素的影响，使得最优设计通常接近约束的边界，没有给不确定因素留够空间。当设计变量由于不确定性发生波动时，最优解将会在约束边界附近变化，有可能落入失效区域。因此，为了保证设计结果可靠性，需要在设计时考虑到可靠性，基于可靠性的多学科优化(Reliability Based Multidisciplinary Design Optimization，RBMDO)正是这样一种设计方法[1-6]。

本文针对传统燃气轮机设计周期长、设计可靠性低的问题，提出基于双循环方法的典型燃气轮机部件多学科可靠性优化设计方法；采用近似技术缩减设计计算规模，提高设计效率；以典型燃气轮机涡轮叶片为例，实现了燃气轮机部件基于可靠性的多学科优化设计，通过与确定性优化设计方法进行比较，验证方法的有效性。

1 循环方法的多学科可靠性设计优化方法

RBMDO是用于改进或提高设计可靠性，或将失效概率降低到一个设定的上限以下的设计优化方法。其基本思想是：要求设计产品在满足一定性能的条件下，使其可靠度达到最大；或者使设计产品达到最佳性能指标时，要求它的工作可靠度不低于某一规定水平。在工程问题中，后者的应用更为广泛，本文的RBMDO也采用后者。

双循环的优化迭代过程分为两个部分，内部是可靠性分析循环，外部是优化循环，使含有可靠性约束的问题得到最优解。可靠性分析嵌套在优化循环中，每次优化迭代需执行多次可靠性分析计算每个概率约束和灵敏度，基于双循环方法的RBMDO过程如图1所示。

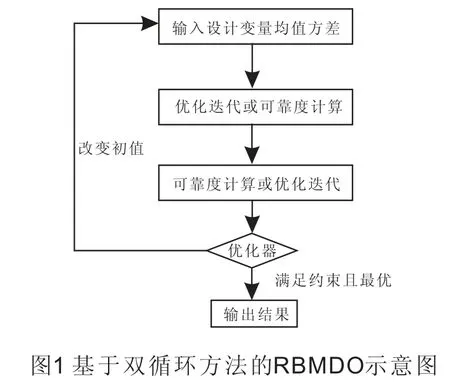
2 Kriging函数的近似模型

目前，工程应用中的近似模型多为多项式响应面模型。该模型多局限于设计空间的局部，同时对非线性程度较高的问题预测效果不够理想。对于燃气轮机RBMDO，涉及的学科和设计变量都比较多，设计空间也很复杂，因此在优化过程中需要使用全局近似模型策略，而Kriging模型正好适用于全局近似；另外，Kriging模型对高度非线性问题的预测效果也明显好于多项式响应面模型。图2、图3为四阶响应面模型和Kriging模型拟合精度对比，从图中可以看到Kriging模型精度明显高于四阶响应面模型。

本文采用Kriging近似模型代替仿真程序进行设计目标寻优。优化流程包括：给定一组基准设计点，使用仿真程序对设计点进行多学科分析，并建立数据库文件，这一过程可通过试验设计完成；通过数据库文件建立Kriging近似模型；使用近似模型在设计空间中进行搜索，得到近似问题的最优解；在最优解处调用仿真程序进行实际的多学科仿真分析；将仿真分析的结果加入数据库文件，更新近似模型；重复，直至收敛。

3 基于可靠性的多学科设计优化技术在燃气轮机设计中的应用

本文采用基于双循环的RBMDO方法对以燃气轮机典型涡轮叶片为例进行优化设计。以燃气总压损失Ploss为优化目标，以叶身最高温度Tmax、叶身平均温度Taver、叶尖最大位移dmax和叶身最大应力σmax为可靠性约束。设定需要达到的可靠度为0.95(β=1.645)。采用雷-菲法对最终优化结果进行可靠性分析。根据试验设计建立优化目标和约束的 Kriging近似模型，通过多学科分析更新近似模型，提高精度。

优化模型：min Ploss

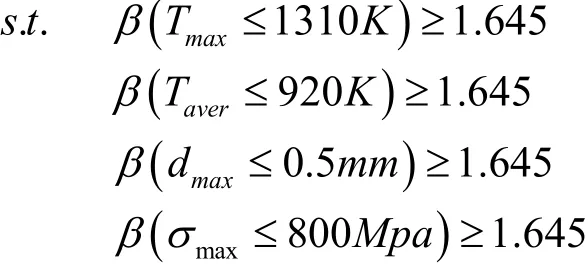
确定性优化与RBMDO结果如表1所示，结果表明，叶尖最大位移、叶身最高温度和叶身平均温度的可靠度达到了99.24% 、99.95%和99.35%，这样的优化结果可以接受。但叶身最大应力的可靠度仅为43.13%，不能满足工程应用要求。有必要进行基于可靠性多学科设计优化。

?

通过RBMDO，叶身最大应力的可靠度提高到了95.73%，优化结果满足可靠性约束的要求。总压损失与与确定性优化相比有所提高，这是由于考虑了不确定因素的影响，在优化过程中牺牲了部分性能以满足可靠性的要求，这也说明RBMDO是一个折中过程，最终使结构性能和可靠性要求达到平衡。叶片经过RBMDO前后的叶尖及叶根截面型线见图4。

4 结论

基于双循环多学科可靠性优化设计方法实现了燃气轮机典型涡轮叶片优化设计，提高了燃气轮机典型部件的综合性能；与确定性优化设计结果比较表明基于可靠性的多学科设计优化方法可以通过牺牲部分性能达到设计可靠性显著提高；基于Kriging函数的近似模型可以显著提高优化设计效率，缩短设计周期。

[1] Dhanesh Padmanabhan, Stephen M. Batill.Decomposition strategies for reliability based optimization in multidisciplinary system design[C].AIAA-2002-5471.

[2] Fan Hui, Li Weiji. An efficient method for reliability-based multidisciplinary design optimization[J]. Chinese Journal of Aeronautics. 2008,(22)： 335-340.

[3] Harish Agarwal, John E. Renaud. New decoupled framework for reliability-based design optimization[J]. AIAA Journal. 2006, 44(7)：1524-1531.

[4] Liping Wang, Srinivas Kodiyalam. An efficient method for probabilistic and robust design with non-normal distributions[C]. AIAA-2002-1754.

[5] Xiaoguan Chen, Timothy K. Hasselman. Douglas J.Neill. Reliability based structural design optimization for practical applications[C]. AIAA-97-1403.

[6] Joongki Ahn, Jaehun Lee, Suwhan Kim, Jang Hyuk Kwon. Sequential reliability analysis framework for multidisciplinary systems[C]. 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference 30 August -1 September. Albany： New York, 2004.