一种用于制导雷达的交互多模型跟踪滤波算法

吴 超，单 奇

(中国电子科技集团公司第三十八研究所，合肥 230088)

0 引言

制导雷达系统是一种由各类探测、控制、数据传输、通信等设备集成的防空导弹武器系统中的地面设备［1］。制导雷达的数据处理分系统需要完成发现目标、形成航迹、识别分类、威胁估计、火控跟踪、杀伤评估等多个任务［2］。其中，数据处理使用的跟踪滤波算法直接决定着雷达形成航迹的精度，影响防空导弹武器系统的杀伤能力，是制导雷达系统研究的核心课题之一。

随着当前第四代战斗机技术的成熟和世界各国现役战斗机向四代机的批量换装，防空导弹系统面临着严峻的挑战。第四代战斗机普遍具备超机动能力，其加速度可达9G左右，战斗机的飞行轨迹在空间位置上可以表现出距离变化率锐减、骤增等现象。这就要求雷达系统具备更高的数据率和高精度的跟踪能力来精确掌控飞机的运动轨迹。

国内外制导雷达数据处理多采用α-β 滤波、卡尔曼滤波、自适应卡尔曼滤波或者交互多模型等方法，在滤波过程中使用CV、CA、Singer 等直线运动模型［3］。使用直线模型逐段拟合目标飞行轨迹的这类型方法在低数据率跟踪弱机动能力的目标时可以获得满意的精度。但是，用于对具备高机动性飞机执行跟踪时，运动模型与机动模式的不匹配将导致跟踪精度的大幅度降低，甚至引致滤波器发散目标丢批，严重制约着防空导弹系统的杀伤性能。

针对上述问题，本文提出了一种用于制导雷达的新的交互多模型跟踪滤波方法。与传统的使用直线运动模型的交互多模型算法相比，本文提出的方法显著提高了跟踪的精度，同时对于目标机动/非机动转换有一定的识别能力和鲁棒的跟踪性能。

1 考虑转弯机动的交互多模型跟踪方法

1.1 UKF-IMM3方法描述

在航迹跟踪中，任意的时刻目标可能进行已知和未知的机动，使得目标运动模式具备不确定性。这种不确定性导致目标机动跟踪成为一个混合估计问题。作为解决混合系统状态估计的次优算法，交互多模型算法(IMM）是国内外雷达数据处理中使用较为普遍的跟踪算法。利用交互式多模型算法对当前时刻目标状态进行估计时，考虑每个模型都有可能成为当前有效的系统模型，每个滤波器的初始条件都是基于前一时刻各条件模型滤波结果的合成。

影响交互多模型算法性能的一个关键因素是目标运动模型集的选择。以往对飞机目标的运动建模中，常选用常速度模型(CV 模型）和Singer 模型［4］。CV模型反映了目标常速度沿直线飞行时的运动状态，Singer 模型反映目标加速度为零均值一阶马尔科夫过程时目标的运动状态。这两种模型的运动方程是线性的，能很好地拟合目标直线航路飞行下一时刻状态与当前时刻状态之间的递推关系。但是，当前各国主力战机都已具备反电子侦察手段，飞行员在获知战机被防空导弹系统锁定的情报时会操纵战机做大范围高强度的机动飞行直至摆脱锁定。在这一系列战术动作中，飞机的航路不再是直线，使用CV和Singer 模型进行跟踪必然精度下降甚至失跟。

因此，本文提出了一种考虑转弯机动的交互多模型滤波(UKF-IMM3）方法。该方法的模型集包括非机动段常速运动模式CV 模型、直线机动模式Singer模型和曲线机动模式常速转弯模型(Constant Turn，CT 模型）。

整个UKF-IMM3 滤波方法的执行流程如图1所示:

(1）对雷达量测作坐标变换，计算变换导致误差的前两阶矩。根据一阶矩对变换后量测进行无偏修正，根据二阶矩构造量测噪声协方差矩阵。

(2）使用3个模型滤波器并行执行当前时刻点迹的滤波，CV和Singer 模型使用卡尔曼滤波器，CT 模型使用不敏卡尔曼滤波器。

(3）根据各滤波器的协方差矩阵分配权重，计算各滤波器输出的加权结果作为对当前点迹的整体滤波输出。

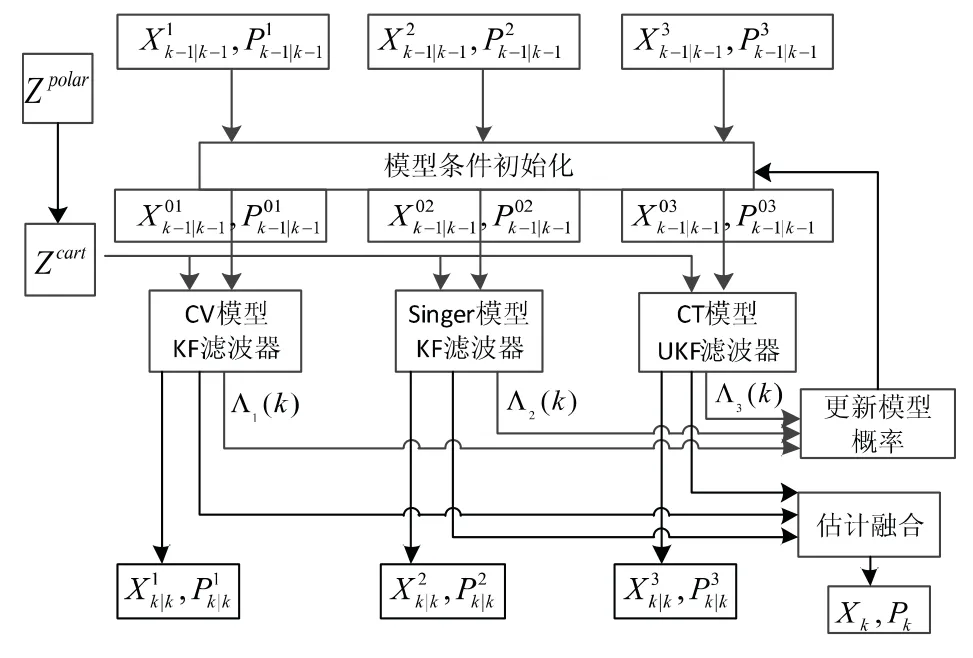
图1 UKF-IMM3 滤波方法的执行流程

1.2 二维修正无偏的量测转换

对于雷达来说，目标的测量通常在空间极坐标系中完成，而后续的量测数据处理是在直角坐标系中完成。在将雷达量测数据用于数据处理之前，需要通过合适的坐标转换方法把量测数据从极坐标系转换到直角坐标系中。Duan［5］等在2004年提出的修正无偏的量测转换是目前从极坐标系到直角坐标系转换的精度较高的计算方法。

对于量测数据距离r、方位θ，其具有距离量测误差~r、方位量测误差~θ，两者相互独立，满足高斯分布，均值为零且标准差分别为δr，δθ。其坐标变换公式为

量测噪声矩阵为

其中

使用修正无偏量测转换之后对于X，Y的数据可以执行后续的解耦滤波。

1.3 交互多模型算法

交互多模型算法是一个递推算法。该算法的一个循环过程如下［6］:

步骤1 输入交互

模型预测概率:

混合概率:

其中i，j=1，…，r。

滤波器初始状态估计:

其中j=1，…，r。

步骤2 模型匹配滤波与预测

卡尔曼滤波:

把滤波结果作为下一时刻与模型Mj相匹配的滤波输入变量，然后每个滤波器按照各自的卡尔曼滤波算法进行状态滤波得到各自的状态估计^Xi(k|k）及协方差矩阵Pi(k|k）。

计算似然函数Λj(k）:

步骤3 模型概率更新

计算模型Mj的后验概率:

步骤4 输出综合

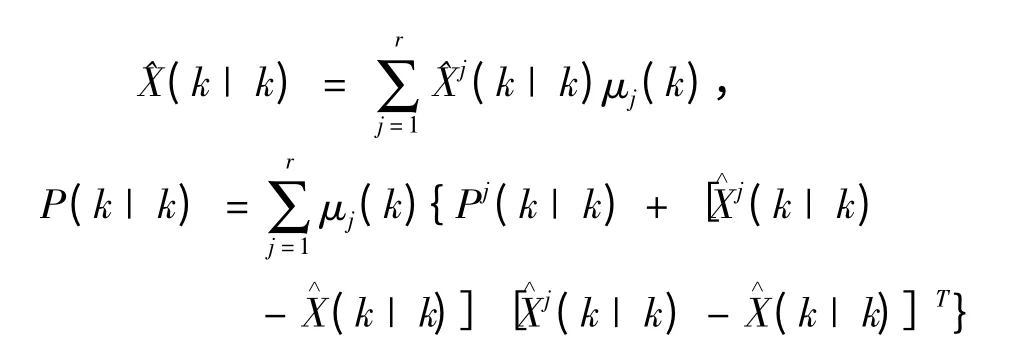
IMM 滤波方法在一个滤波周期内同时进行多个基于不同目标运动模型的滤波器工作的算法，该算法整体状态估计通常为多个滤波器状态估计的有效混合。通过同时使用多个模型，有效的解决了估计过程中由于目标模型的不确定性而带来的困难。

1.4 不敏卡尔曼滤波(UKF）

UKF 是基于不敏变换发展起来的。它通过一组确定大小的样本点来反映状态向量的分布，经过任意非线性函数转换后，这些样本点仍能够很好地反映状态的分布，从而精度可以逼近2 阶以上［7］。详尽的UKF算法步骤可以参见文献［8-9］。

2 运动模型

2.1 CV 模型

离散化后二维CV 模型的时间系统表达式为

其中，ω(k）是均值为零、方差为δ2的高斯白噪声。

2.2 Singer 模型

Singer 模型把机动噪声作为有色噪声建立数学模型，认为目标加速度是具有指数自相关的零均值随机过程。

离散化后二维Singer 模型的时间系统表达式为

其中，ω(k）是零均值白噪声过程;方差为2ασ2，σ2为机动加速度方差，α 是机动时间常数τ的倒数，其取值依赖于机动时间持续长短。

2.3 CT 模型

由于武器系统应对的多是敌方目标，在缺乏目标类型的先验知识的情况下，敌目标机动能力无法确定，也就不能得到敌目标圆周运动的角速度先验，所以本文的滤波算法中加入了未知转弯角速度ω的CT 运动模型［10］。

在未知转弯角速度ω的CT 模型中，目标转弯角速度作为状态向量中的一个分量需要估计。此时扩展的目标状态向量为

离散二维CV 模型的时间系统表达式为

3 仿真实验

实验采用Matlab (2008a）软件进行仿真计算。实验场景包含了对目标9G 加速度的机动规避和多次机动的仿真模拟。仿真产生的航迹数据加入量测噪声，假设雷达距离量测精度为60 m，方位角量测精度为0.1°，跟踪数据率为16 Hz。实验中对本文提出的使用CV、Singer、CT 运动模型的交互多模型不敏卡尔曼滤波算法(UKF-IMM3算法）与现有的使用CV、Singer 运动模型的交互多模型卡尔曼滤波算法(KFIMM2算法）采用蒙特卡罗仿真(独立运行100 次）进行对比分析。

3.1 实验场景1

在航路仿真的过程中，目标飞行速度设置为1260 km/h。假设雷达站处于坐标原点，目标从(137 km，143 km）处进入，向站直线飞行80 km，然后以9 G的加速度逆时针转半圈，之后背站直线飞行20 km，再以9G的加速度顺时针转半圈，最后直线飞向雷达站。其中一次仿真加噪的航路如图2所示。

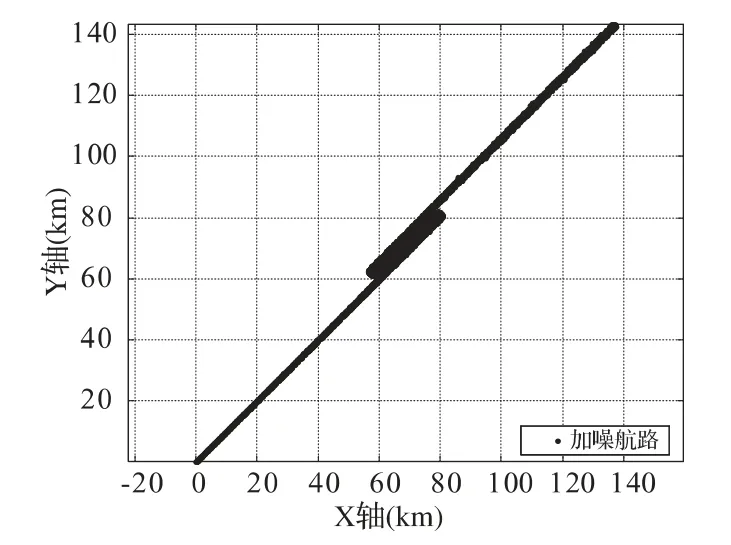
图2 场景1 航路仿真图

在模型状态方程的设计上，CV 模型选择小的噪声方差qcv=1e－6以准确模拟直线飞行;Singer模型选择噪声方差qsinger=1和α=1/20 提高模型的适应性，避免滤波发散;由于CT 模型的先验角速度不可靠，所以设置大的噪声方差qcT=1。

图3 显示了跟踪场景①航路时UKF-IMM3算法各模型的概率变化。在320 s 附近和410 s 附近，CT模型的概率明显上升达到3个模型概率的最大值，此时正是目标进行机动转弯的时刻;其余时间CV 模型和Singer 模型的概率都大于CT 模型(CV 模型的概率大于Singer 模型），符合目标进行直线飞行的运动状态。

图3 场景1 跟踪UKF-IMM3 各模型的概率

图4 是两种算法对场景1 跟踪的X和Y 位置均方根误差图(实验数据图中的曲线根据16 Hz为刻度的数据点绘制，为了图形的清晰，仅在每隔10 s的数据点画上标识符号，下同）。其中加号线是量测的误差曲线，叉号线是KF-IMM2的误差曲线，圈号线是UKF-IMM3的误差曲线。经过10 s后两种算法逐步收敛。在300 s 前KF-IMM2算法优于UKF-IMM3算法。到了320 s和410 s 附近，目标进行快速机动，KFIMM2算法的模型失配，导致均方根误差有两次大的跃升，其后精度一直差于UKF-IMM3算法;而UKFIMM3算法包含了处理机动的CT 模型，其均方根误差在这两个时间点没有大的波动，整个跟踪过程中误差曲线基本光滑。

图4 场景1 跟踪的位置均方根误差

图5 是两种算法对场景1 跟踪的X和Y 速度均方根图。其中叉号线是KF-IMM2 速度误差曲线，圈号线是UKF-IMM3 速度误差曲线。在10 s 钟跟踪之后，两种算法逐步收敛。到了320 s和410 s 附近，KFIMM2算法的均方根误差有两次大幅度的跃升，同时UKF-IMM3算法的均方根误差也发生跃升，但是跃升幅度小于KF-IMM2。整体而言，UKF-IMM3的速度均方误差小于KF-IMM2的误差。

图5 场景1 跟踪的速度均方根误差

表1 记录了场景1中两种算法跟踪全过程的X、Y坐标位置反算回雷达极坐标系后计算得到的全局的距离均方根误差和全局的方位均方根误差。在直线飞行段，UKF-IMM3的距离和方位精度不如KF-IMM2;在机动飞行段，UKF-IMM3的精度则好于KF-IMM2。全局来看，UKF-IMM3 距离误差是量测误差的24.5%，方位误差是量测误差的20.0%;与KF-IMM2 相比，距离误差减小了11.9%，方位误差减小了33.3%。

表1 场景1 跟踪距离和方位的均方根误差对比

3.2 实验场景2

为了模拟实战中敌方目标躲避我方雷达锁定的战术动作，仿真了目标高加速度多次机动的航迹:目标开始时从150 km 远处向站飞行，直线飞行1 min后以9G加速度逆时针转一个整圆，而后直线飞行1 min 再以9G 加速度顺时针转整圆，继续重复如上运动2 次，最后向站飞行1 min。目标保持1260 km/h的恒定线速度。其中一次仿真加噪的航路如图6所示。

图6 场景2 航路仿真图

图7 显示了跟踪场景2 航路时UKF-IMM3算法各模型的概率变化。在整个跟踪过程中，CT 模型的概率有6 次明显超过CV和Singer 模型的概率之和，符合目标6 次机动的运动模式。

图7 场景2 跟踪UKF-IMM3 各模型的概率

图8 是两种算法对场景2 跟踪的X和Y 位置均方根误差图。跟踪10 s后两种算法逐步收敛。在整个跟踪过程中，KF-IMM2算法的均方根误差有6 次明显的跃升，对应目标进行机动时KF-IMM2的运动模型与实际运动模式失配;而UKF-IMM3 由于包含CT 模型可以光滑的处理目标机动过程。经过6 次机动，UKF-IMM3的位置均方根误差明显小于KF-IMM2的误差。

图8 场景2 跟踪的位置均方根误差

图9 是两种算法对场景1 跟踪的X和Y 速度均方根图。在目标做6 次机动的时刻，KF-IMM2算法的速度误差都有大幅跃升;在机动时刻UKF-IMM3算法的速度误差也有增大，但是增大幅度小于KF-IMM2。从第1 次机动开始，KF-IMM2的X 坐标速度的误差明显大于UKF-IMM3，同样的，KF-IMM2的Y 坐标速度的误差也略大于UKF-IMM3。

图9 场景2 跟踪的速度均方根误差

表2 记录了场景2中两种算法跟踪全过程的X，Y 坐标位置反算回雷达极坐标系后计算得到的全局的距离均方根误差和全局的方位均方根误差。在机动段，UKF-IMM3算法精度的提升非常明显。全局上，UKF-IMM3 距离误差是量测误差的32.2%，方位误差是量测误差的20.0%;与KF-IMM2 相比，距离误差减小了46.4%，方位误差减小了66.7%。

表2 场景2 跟踪距离和方位的均方根误差对比

实验结果显示，在高数据率跟踪时UKF-IMM3 对目标快速机动的反应能力比KF-IMM2 更强。在目标作快速机动时，通过直线来拟合机动曲线的KF-IMM2算法对于每个机动转弯都会产生较大的跟踪误差，出现的时机就在目标的距离变化率由正转负或是由负转正时;而使用UKF-IMM3算法使用的CV、Singer、CT 模型集则更好地拟合了目标的运动模式，特别是在目标执行多次快速机动时CT 模型的介入明显减小跟踪的误差。

4 结束语

跟踪制导雷达要求数据处理软件能直接跟武器系统铰链，直接引导武器系统去打击目标，所以要求数据处理软件跟踪精度高，跟踪延迟小，稳定度高。而跟踪滤波正是影响制导雷达数据处理跟踪精度的关键问题。本文提出一种使用未知角速度ω的CT 模型的交互多模型(UKF-IMM3）跟踪方法，此方法具有如下优势:

(1）采用交互多模型的结构，适合跟踪目标机动/非机动飞行的全过程。

(2）针对现有的算法使用直线模型来拟合机动曲线，难以精确跟踪目标快速机动的问题。UKF-IMM3通过加入未知角速度ω的CT 模型，更好的拟合缺乏先验信息目标的运动模式，适合于防空系统对敌方目标直线段和机动段的全过程跟踪。

(3）现有的跟踪方法使用线性滤波器跟踪会引入较大的线性误差，而本文的方法通过使用不敏卡尔曼滤波具备更好跟踪精度。

仿真实验设计了两个实验场景，包含了目标执行蛇形规避和多次快速机动的仿真。与现有的以直线拟合机动的滤波算法相比，本文提出的方法显著地提高了跟踪精度，同时在目标转入机动的时刻具有一定的识别能力和鲁棒的跟踪性能。今后的工作集中在对于UKF-IMM3算法速度跟踪性能上的调优，以及算法向工程应用的转化。

［1］黄槐，齐润东，文树梁.制导雷达技术［M］.北京:电子工业出版社，2006.

［2］王小谟，张光义.雷达与探测——信息化战争的火眼金睛［M］.2 版.北京:国防工业出版社，2008.

［3］何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.2 版.北京:电子工业出版社，2009.

［4］Li X R，Jilkov V P.Survey of Maneuvering Target Tracking Part I:Dynamic Models［J］.IEEE Trans on Aerospace and Electronic Systems，2003，39(4）:1333-1364.

［5］Duan Z S，Han C Z，Li X Rong.Comments on“unbiased converted measurements for tracking”.IEEE Trans.on Aerospace and Electronic Systems，2004，40(4）:1374-1377.

［6］Li X R，Jilkov V P.Survey of Maneuvering Target Tracking Part V:Multiple-Model Methods［J ］.IEEE Trans.on Aerospace and Electronic Systems，2005，41 (4）:1255-1321.

［7］Julier S J，Uhlmann J K.Unscented Filtering and Nonlinear Estimation［J］.Proc.of the IEEE，2004，92 (3）:401-422.

［8］单奇，钮俊清，李川.炮位侦校雷达的数据处理研究［J］.雷达科学与技术，2010，8(2）:171-176.

［9］钮俊清，单奇，任清安，等.跟踪弹道导弹全阶段的可变多模型方法［J］.雷达科学与技术，2011，9(3）:224-231.

［10］韩崇昭，朱洪艳，段战胜，等.多源信息融合［M］.2 版.北京:清华大学出版社，2010.