基于共轭梯度法的降低多载波信号峰均比的研究

徐 壮，竺小松，李陈磊

(合肥电子工程学院，合肥 230031)

0 引言

多载波信号传输技术由于其频谱利用率高、抗干扰能力强的特点，在通信系统中有着广泛的应用，例如用于多载波雷达系统、JTIDS 干扰系统以及各种频率分集系统等［1-2］。由于多载波信号是由多个正弦子载波组成，随着子载波数的增加，其波形的幅值呈高斯分布，会形成高于平均幅度的时域尖峰，也就是峰值功率。一般情况下，载波数目N 越大，峰值功率也越大。为了不失真地传输这些高峰值功率的多载波信号，发送端对高功率放大器的线性度要求很高，同时接收端对前端放大器以及A/D 变换器的线性度要求也很高且输出效率很低。

峰值功率很大程度上取决于正弦子载波的初始相位，多载波信号以相同相位相加时会产生高于平均幅度的时域尖峰，不同相位相加时会使信号的平均幅度下降。因此，通过采取寻找最佳的正弦子载波初始相位的办法，可以有效地降低信号的峰值功率。已有许多文献［3-5］对寻找最佳的初始相位序列进行了研究。1954年，Shapiro和Rudin 提出了一种相位序列［3］，当子载波数为2的幂次时，PAPR 降至3 dB左右。1965年，Newman 提出了一种相位序列［4］，当子载波数为3时，其性能最差，PAPR 达到3.68dB，但随着子载波数的增加，其PAPR 逐渐收敛于2.6 dB。1994年，S.Narahashi 提出了一种相位序列［5］，其性能与Newman相位序列接近，只是当子载波数小于6时，其性能稍优于Newman 相位序列。由于Newman 相位序列和Narahashi 相位序列都是在N 趋向无穷大时通过逼近理论推导出来的，在N的取值不是很大的情况下，其结果并不理想。本文采用共轭梯度法对Newman 相位序列进行了优化，并对其结果与Newman 法和Narahashi 法所得的结果进行了比较。

1 两种著名的初相优化方案

N个多载波信号相加可表示为

为了方便讨论和分析，假设Ak在整个时间域中相等，则s(t）的瞬时功率为

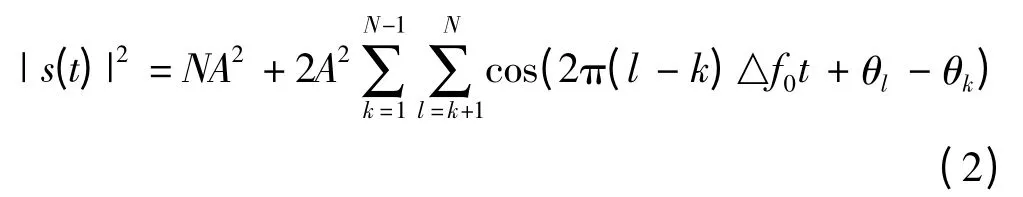
根据PAPR的原始定义得

其中

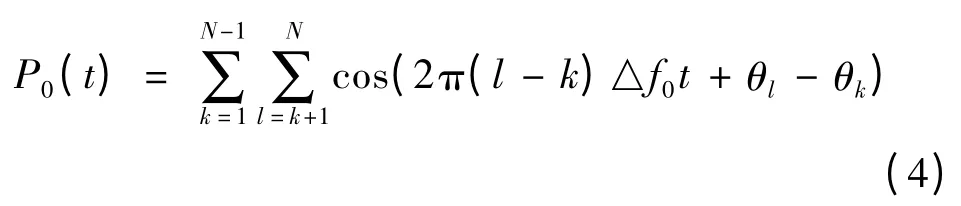
Newman 相位

Narashina 相位

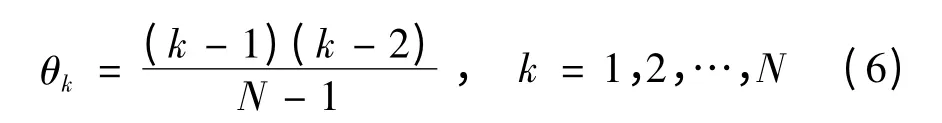
表1分别给出了当N 不同时采用Newman 法和Narahashi 法所求得得PAPR 值［6］。

2 共轭梯度算法原理

共轭梯度法是利用目标函数梯度逐步产生共轭方向作为线搜索方向的方法［7］，每次搜索方向都是在目标函数梯度的共轭方向上，搜索步长通过一维极值算法确定。

表1 不同方法的PRPR 结果比较

共轭梯度法搜索的第一步是沿负梯度方向。从任意点X(k）出发，按S(k）=－▽f (X(k））方向找到X(k+1），设按S(k+1）=－▽f (X(k+1））+βkS(k）来产生搜索方向。

在上式中βk的选择上，应使n 维欧氏空间En中的两个非零向量S(k）与S(k+1）关于矩阵A 共轭。即

以AS(k）乘以两边，于是有

由(7）、(8）两式可得

由于计算不方便，通过简化可得

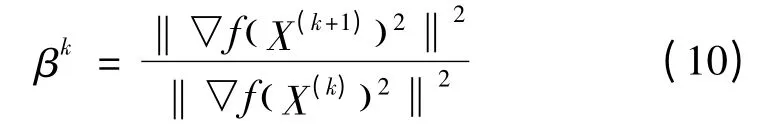
综上所述，N 维目标函数共轭梯度搜索可表示为

3 基于共轭梯度法降低多载波信号的峰均比

求解峰均值过程可以等价为寻找使得P0(t）最小的{θk}的过程，但是实现的过程是非常困难的。为了便于用共轭梯度法进行搜索，进行了下列数学分析推导［8］。根据施瓦兹不等式有下列不等式成立:

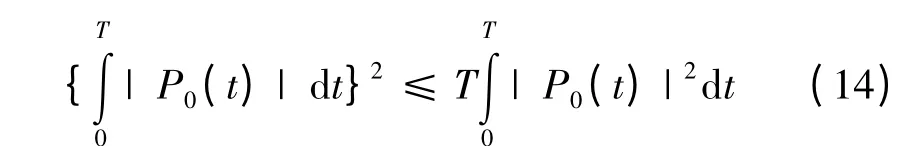
由方差公式 D [ X ]=E [ X2]－E2［X］，则EP0(t）的方差δ2为

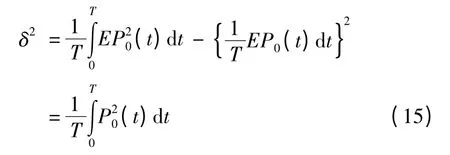
由(14）、(15）两式得

可见，如果δ2能够取得最小，就可以推出P0(t）此时也是最小，而δ2最小是一个多参数(含θ1θ2…θN）的目标函数，即转化为用共轭梯度法求无约束多维极值问题minδ2，θk∈Rn。

具体的算法步骤如下:

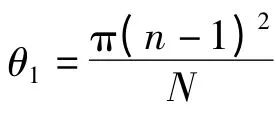
(2）若‖▽δ2(θ1）‖≤ε，停止，极小值点为θ1，否则转步骤(3）;

(3）取p1=－▽δ2(θ1）;

(5）若‖▽δ2(θk+1）‖≤ε，停止，极小值点为θk+1，否则转步骤(6）;

(6）若k+1=n，令θ0=θn，转步骤(3），否则转步骤(7）;

4 仿真分析

在matlab的开发环境下，分别仿真计算了子载波数N=2～36时信号s(t）的幅值和PAPR(dB），设共轭梯度法的搜索精度ε=10－6、s(t）的幅值A=1。在同等情况下，与Newman方法和Narahashi方法进行了性能比较。

图1为载波数2≤N≤36时3 种算法降低PAPR的比较图。如图1所示，在N ≤10的情况下，共轭梯度法求的PAPR 要明显低于Newman 法和Narahashi 法所得的PAPR 值。

图1 3 种算法PAPR 比较

图2为载波数N=16时3 种算法的振幅瞬时包络图。从图中可看出，文中的算法能更有效地改善多载波的包络特性。

图2 N=16时多载波信号的包络图

5 结束语

本文分析了抑制多载波高峰均值的相位组合理论，推导简化了初始相位来降低峰均值的公式，将峰均比的抑制问题转化为N 维变量的寻优问题。结合共轭梯度法收敛速度快、稳定性高的优点，将其成功地运用到峰均比抑制的问题上。实验仿真表明，在不过分增加复杂度的情况下，新方法要优于Newman 法和Narahashi 法。从图1 可看出，随着N的增加，其峰均值要比Newman 法低0.2～0.3 dB。从图2 可看出，文中的算法能更有效地改善多载波的包络特性，使其包络更具有平稳性。

［1］D R Gimlin，C R Patisul.On minimizing the Peakto-average power ratio for the sum of N sinusoides［J］.IEEE Transactions on Communications，1993，41(4）:631-635.

［2］P Chaudury，W Mohr ，S Onoe.The 3GPP proposal for IMT-2000［J］.IEEE Communication Magazine，1999，37(12）:72-81.

［3］Boyd Stephen.Multicarrier signals with low crest factor ［J］.IEEE Transactions on Circuits and Systems，1986，33(10）:1018-1022.

［4］D J Newman.An L1 external problem for polynomials［J］.Proc.Amer.Math.Soc.1965，16(5）:1287-1290.

［5］S Narahashi，T Nojima.New phasing scheme of N-multiple carriers forreducing peak-to-average power ratio ［J］.Electronics Letters，1994，30(17）:1382-1383.

［6］江涛.OFDM 无线通信系统中峰均功率比的研究［D］.武汉:华中科技大学，2004.

［7］郭科，陈聆，魏有华.最优化方法及其应用［M］.北京:高等教育出版社，2007.

［8］S Narahashi，K Kumagai，T Nojima.Minimising peak-to-average powerratio of multitone signals using steepest descent method［J］.IEEE Electronics Letters，1995，31(18）:1552-1554.