舰船雷达设备的冲击响应计算方法研究

陈 杨

(中国船舶重工集团公司第七二四研究所，南京 210003)

0 引言

多体系统是指通过一定方式相互连接的多个刚体或者刚体与弹性体的复杂系统。近年来，多体系统的动力学问题被受到普遍关注，如何建模和数值解析是对其研究的主要内容。多体系统的位形空间的位数增大，使得动力学方程的维数也增大，加上多种系统的耦合等因素使动力学方程出现刚性问题，提高动力学问题求解的精度和稳定性变得越来越重要。

三维多刚体系统与二维多刚体系统相比运动分析比较复杂，但求解方法相似，也是由位置坐标和方位坐标组成。位置坐标表示较为固定，是由坐标系基点坐标来确定;方位坐标则具有多种不同的形式，如方向余弦矩阵、欧拉角、卡尔丹角、有限转动四元数、欧拉参数等，最常用的是欧拉角和欧拉参数。

对多柔体系统动力学响应的求解最早是采用运动-弹性动力学方法，即KED(Kinetic Elastic Dynamic Amasses）法［1］。该法不考虑构件的弹性变形对其大范围运动的影响，通过对多刚体系统动力学分析得到构件运动特性，且考虑构件的惯量特性，以惯性力的形式加到构件上，根据惯性力和系统外力对构件进行弹性变形和强度、刚度的分析，实质上是把多柔体系统转变为多刚体系统和结构动力学分析的简单叠加。该方法不能满足轻质、高速的现代机械系统的动力学分析。为了能够更加真实地分析多柔体系统的机械特性，考虑弹性变形对大范围运动的影响，人们提出用混合坐标来描述柔性体变形［2］。建立浮动坐标系，将构件的变形看作是浮动坐标系的大范围运动与相对于该坐标系的变形的叠加，用大范围浮动系的刚体坐标与柔性体的节点坐标建立系统的动力学模型。

1 多刚体系统动力学方程建立

针对不同复杂的机械系统模型，建立系统的拉格朗日运动方程，对任意刚体建立6个广义坐标带乘子的拉格朗日方程及相应的约束方程［3］:

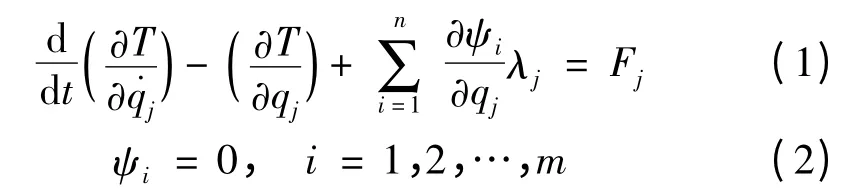
式中，T为系统的总动能，qj为描述系统的广义坐标，ψi为系统的约束方程，Fj为在广义坐标方向上的广义力，λj为m×1的拉格朗日乘子列阵。

式(1）、(2）可以改写成下面的形式:

动能可以定义为

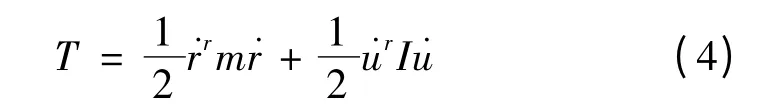
代入以上方程中，整理成简化的矩阵形式，可以得到

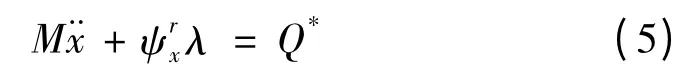
式中，x=(x1，x2，…，xn）T，ψ=(ψx1，ψx2，…，ψxn），M和Q*分别为系统的6×6 广义质量对角阵和6×1 广义列阵。

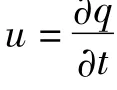
由以上可知，对于多刚体系统，把力和加速度联系在一起得到6个一阶动力学方程。

式中q=(x，y，z，ψ，θ，φ）T。

6个一阶运动学方程，将位置和速度联系在一起:

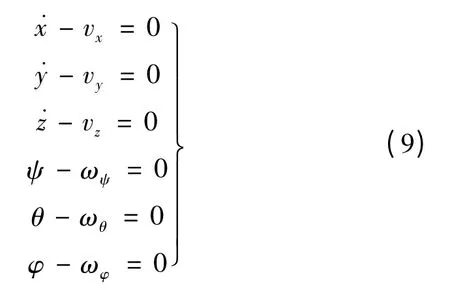
另外，还有约束代数方程、外力定义方程以及自定义的代数微分方程。

式中，u为广义坐标的微分，f为外力和约束组成，t 是时间。

若令y=[q，u]T为状态向量，那么系统方程可以改写为

2 多柔体系统动力学方程建立

柔性体动力学的建模方法与多刚体系统动力学相似。根据选取的参考坐标系不同，柔性体建模可以分为3类:浮动坐标系方法、随转坐标系方法和惯性坐标系方法［4］。浮动坐标系法使多刚体动力学软件扩展应用于多柔体系统成为可能，是目前多柔体系统建模中广泛使用的方法。

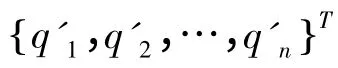
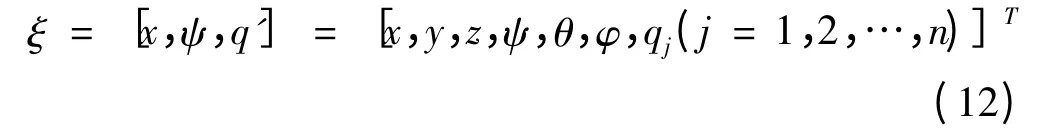
柔性体的动力学方程可以从拉格朗同方程导出［5］:

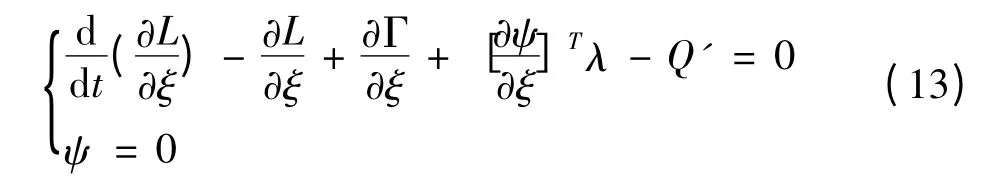
式中，ψ为约束方程;λ为对应于约束方程的拉氏算子;Q'为投影到ξ 上的广义力;L为拉格朗日项，定义为L=T－W，T、W分别为系统的动能和势能;Γ为能量消耗函数。

将所得到的T、W、Γ 代入式(13），求得最终的运动微分方程为

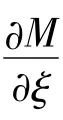
3 算例

本文以通用型雷达天线框架为例进行刚柔耦合多体动力学冲击响应计算。天线框架在收到冲击载荷时，主要是由于自身重量和TR组件的重量产生的惯性力使得天线框架产生冲击响应，并产生变形。TR组件与框架之间的连接靠其他连接件过渡，连接件最终传递给TR 框架的力矩通过螺钉螺栓转换为三方向的受力。TR组件结构强度相对较大，可以忽略其自身的变形。另外，由于天线框架靠基座法兰与基座螺栓连接，可以忽略其基座法兰的变形。

3.1 模型约束条件及载荷

为提高计算效率，减少计算时间，将采用刚柔耦合计算的方法，对主要研究对象天线骨架进行离散化处理，将骨架内的TR组件简化刚性体。天线框架与基座法兰进行固定连接;基座法兰设置冲击响应驱动;TR组件与天线框架设置6 自由度的柔性连接。如图1所示。

图1 天线框架约束设置示意图(隐藏TR组件）

设备在作战和航行时应能耐受舰船自身武器发射、非接触性爆炸或高强度碰撞等非重复性的强烈冲击，并连续有效地工作。冲击载荷参照《舰船环境条件要求 机械环境》(GJB1060.1-91）计算求得。

3.2 计算结果及分析

天线框架在受到横向冲击时，最大应力出现在中间立柱部分，为14.6 MPa，如图2所示;天线框架在受到纵向冲击时，最大应力出现在反射面法兰后部的立柱部分，为13.0 MPa，如图3所示;天线框架在受到垂向冲击时，最大应力也出现在反射面法兰后部的立柱部分，为39.3 MPa，如图4所示。

图2 天线框架受横向冲击时应力分布图

图3 天线框架受纵向冲击时应力分布图

图4 天线框架受垂向冲击时应力分布图

4 结束语

本文主要研究了舰船雷达设备的冲击响应计算方法，并以通用型雷达天线框架为例进行仿真计算，求得了天线框架在强冲击载荷条件下的应力响应分布情况。希望在以后的工作中，继续将仿真计算与试验验证相结合，整理出一套准确、可靠的计算方案，为舰船雷达设备的抗冲击设计提供技术指导。

［1］Schiehlen W.Multibody system dynamics:Roots and perspectives［J］.Multibody system Dynamics，1997(l）:149-188.

［2］Likens P W.Finite element appendage equation for hybrid coordinate dynamic analysis［J］.Journal of Solids ＆ Structures，1972(8）:709-731.

［3］杨辉.刚柔耦合动力学系统的建模理论与试验研究［D］.上海交通大学博士学位论文，2002.

［4］WASFY T M，NOOR A K.Computational strategies for flexible multibody systems［J］.Appl Mech Rev，2003，56(6）:553-613.

［5］刘铸永.刚柔耦合系统动力学建模理论与仿真技术研究［D］.上海交通大学博士学位论文，2008.