零点和极点位于有限条射线上的亚纯函数的增长性
叶枝宏,石东伟
(1.普洱学院数学系,云南普洱665000;2.河南科技学院,河南新乡453003)
零点和极点位于有限条射线上的亚纯函数的增长性
叶枝宏1,石东伟2
(1.普洱学院数学系,云南普洱665000;2.河南科技学院,河南新乡453003)
研究了一类亚纯函数级的估计问题,得到了零点位于从原点出发的有限条射线,极点位于其他从原点出发的有限条射线上的亚纯函数级与下级,没有类似于此类整函数的级与下级的估计关系.
亚纯函数;零点和极点;级与下级
1 亚纯函数概述和主要结论
本文假设读者已经熟悉了Nevanlinna理论中的主要结果和相关记号,并统一用ρf(λf)表示函数f(z)的级(下级),简记为ρ(λ).此外,详细内容可参考文献[1-3].
对于零点和极点位于有限条射线上的亚纯函数,乔建永在文献[4]中证明了:
定理A如果亚纯函数f(z)的零点位于arg z=θj(j=1,2…,q)则
笔者近期在文献[5]中证明了:
定理B存在的亚纯函数f(z),满足:
(1)零点和极点位于有限条(一条)射线上;
(2)级为+∞,下级为0;
(3)只有有限条Julia方向.
而定理B证明中所构造的亚纯函数函数的零点和极点位于同一条射线上.一个比较自然的问题是当零点和极点所在射线不同时,级与下级之间是否有一种具体的围界式子.对于只有2条射线的情况,在文献[6]中证明了:
定理C设亚纯函数f(z)的零点位于arg z=α,极点位于arg z=β(,α≠β),那么它的级和下级满足ρ≤[λ]+2.
猜测一般情况可能具有ρ≤[λ]+m的估计(m为射线条数),进一步否定了这个猜测.具体而言得到如下定理:
定理1对于任何s∈N,必存在α1, α2, α3,β1, β2, β3∈[-π,π)和一零点位于射线arg z=α(jj=1,2,3),极点位于射线arg z=β(jj=1,2,3)上的亚纯函数(fz)满足ρf-λf>s.
2 几个辅助结论以及证明
定义设D=D(α1,α2,....,αm)表示从原点出发的射线族Dl=D(lα1,lα2,....,lαm),l∈N; 用G(Dl)表示集合的凸包(开),并记V(D)={l∈N∶0∉G(Dl)}.
引理1设D=D(α1,α2,....,αm)和F=F(β1,β2,....,βm)两判别的射线族,如果存在自然数q,q'使得{q,q+1,...,q'}∩V(D)=φ,并且{q,q+1,...,q'}∩V(F)=φ,则存在一零点位于D,极点位于F上的亚纯函数,满足λ<q≤q'<ρ.
引理1的证明需要下面的引理:
引理2给定m, q, s∈N;βμl∈(0,+∞),1≤μ≤m,0≤l≤s -1,则存在有穷的正数序列xμj,1≤j≤n(μ),1≤μ≤m,满足,这里n(μ)是有限数,并且不失一般性设0<xμj<1[7].
引理1的证明:
设q,q'使得{q,q+1,...,q'}∩V(D)=φ,并且{q,q+1,...,q'}∩V(F)=φ成立的自然数.运用引理2和V(D)和V(F)的定义,对于D=D(α1,α2,....,αm),存在βμl,使得
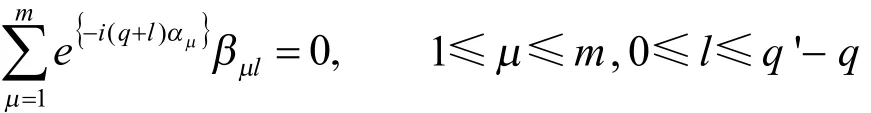
对于F=F(β1,β2,....,βm),存在βμl',使得

对于βμl,βμl',存在0<xμl<1和0<yμl<1,满足

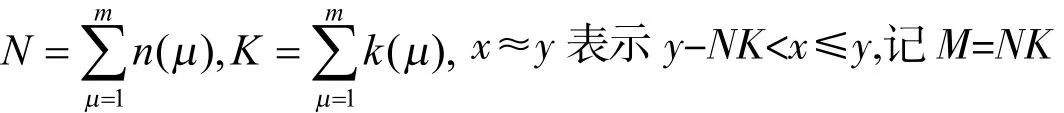
下面构造递增趋于+∞的数列{tv}和{Nv},Nv是M的整数倍.
对于λ∈(q-1,q);ρ∈(q',q'+1),选取适当的t,使0按如下递推的方式定义:
当v是奇数时选取Nv≈2(Ctv)λ.
当v是偶数时Nv的选取如下:
N2≈2(Ct2)ρ.如果t4>e2Ct2,选取N4≈2(Ct4)ρ.否则选取N4≈2(Ct4)λ.
依次下去:如果tv><v, k是使得Nk≈2(Ctk)ρ,且与v最近的偶数)选取Nv≈2(Ctv)ρ,否则选取的v必然有无穷多项.记
显然有Ctv<tv+1,又因为C≥A,C≥B,所以区间[tv,Btv]对于每一个都不相交,区间[tv,Atv]对于每一个v也不相交;
记n1(t)=n1(t,Z),n2(t)=n2(t,Y)
构造的n1(t),n2(t)具有以下性质(设A≥B)

下面构造以{aj},{bj}为零点,以p'为亏格的典型乘积E1(z)和E2(z),并构造亚纯函数
选取r∈[A-1exp(At),Alnt]∩[B-1exp(Bt),Blnt ],显然上面的交集非空且r∉[t,Ct ],
vn vn+1vn vn+1vn vn
r∉[tvn,Atvn],r∉[tvn,Btvn].选取充分小ε0的使得区间[r, r+ε0)内没有(fz)的零点和极点.在|z|≤r<r+ε0(ε0是充分小的固定正数)内
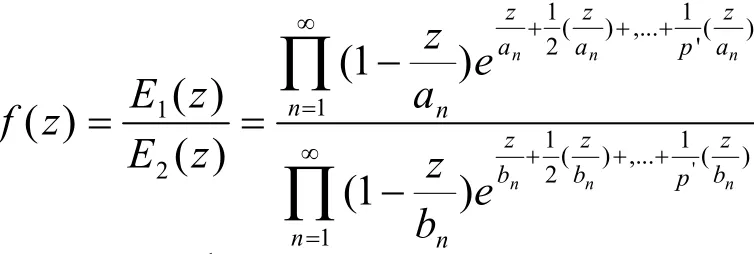

没有零点和极点,于是LogF(z)可以单值解析分支,选取主值分支logF(z)(选取的原因是后面的运算与虚部无关).此时在原点的充分小领域内
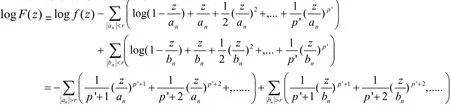

于是得到
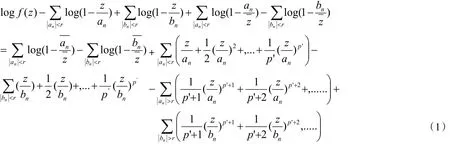
对式(1)两边取实部得到

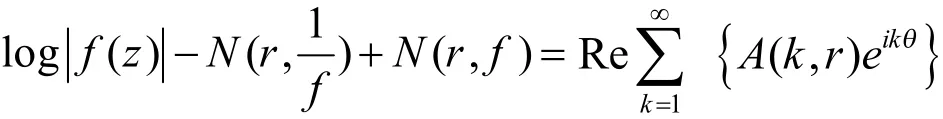
其中

所以
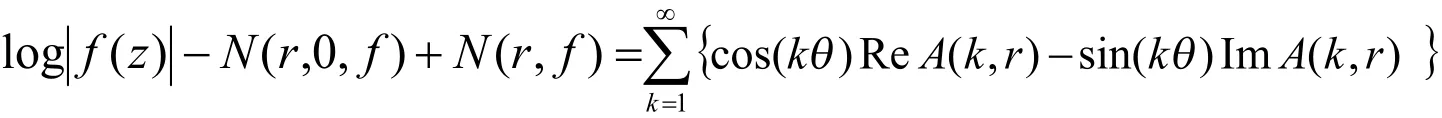
进一步来估算A(k,r).
(1)当q≤k≤q'时,由引理1有

由于


(2)当利用这些关系式子得到


从而所构造的函数以λ为下级,以ρ为级,且λ<q≤q'<ρ.
3 借助辅助引理证明定理1
根据引理3对于任意的s∈N,存在q∈N,使得2q-1>s,记q'=3q -1>q+s,我们考虑射线族和射线,其中,容易看到{q,q+1,...,q'}∩V(D)=φ,且{q,q+1,...,q'}∩V(F)=φ.
由上面的定理知道存在亚纯函数(fz)满足λ<q≤q'<ρ,即ρ-λ>q'-q =s.
定理说明对于一般情况ρ≤[λ]+m的估计不成立.
证毕.
[1]陈特为,张锡桐.圆外亚纯函数的Nevanlinna理论[J].华南师范大学学报:自然科学版,2002,11(4):40-44.
[2]张南岳,陈怀惠.复变函数选讲[M].北京:北京大学出版社,1995:53-78.
[3]Lee A.Rubel,Entire and Meromorphic Funcions[M].Spinger,1996:78-86.
[4]Qiao J Y.Tow problems in the value distribution theory[J].Acta.Mathematics sinia Newseries,1995,11(4):365-369.
[5]叶枝宏,刘满霞.零点和极点位于有限条射线上的亚纯函数[J].云南师范大学学报:自然科学版,2007,8(增1):18-20.
[6]叶枝宏,尹爱军.一类亚纯函数的级[J].华南师范大学学报:自然科学版,2010,24(2):24-26.
[7]Gleizer E V.Growth of entire functions with zeros on a syetm of rays[J].Ukrainskii Matematicheskii Zhurnal,1996,38(3):292-302.
(责任编辑:卢奇)
Growth of Meromorphic functions with zeros and poles lie on finitely many rays
Ye Zhihong1,Shi Dongwei2
(1.Department of Mathematics Puer College,Puer 665000,China;2.Henan Insititute of Science and Technology,Xinxiang 453003,China)
A question about the order and the lower order of meromorphic functions with zeros lie on finitely many rays and poles lie on finitely many other rays will be answered.Relation the order and the lower order of those meromorphic functions different from entire functions with zeros lie on finitely many rays.
Meromorphic function;order and lower order;zeros and poles
O174.52
A
1008-7516(2013)05-0040-05
10.3969/j.issn.1008-7516.2013.05.010
2013-06-24
云南省教育厅科学研究基金资助项目(2012c170)
叶枝宏(1980-),男,云南普洱人,硕士,讲师.主要从事复分析研究.

