基于DV-HOP算法的提高定位精度研究

张佳,刘艳昌,王鲜芳

（1.河南科技学院,河南新乡453003；2.河南师范大学计算机与信息技术学院,河南新乡453007）

基于DV-HOP算法的提高定位精度研究

张佳1,刘艳昌1,王鲜芳2

（1.河南科技学院,河南新乡453003；2.河南师范大学计算机与信息技术学院,河南新乡453007）

无线传感器网络在目标追踪、环境监测到空间探索等方面得到广泛应用,其关键支撑技术之一是节点定位.以经典的DV-HOP算法为研究对象,为突破算法本身的计算应用条件限制,在使用最小二乘原理得到位置信息时,采用异方差消除原理,在参考节点位置信息存在明显误差时,提高未知节点的定位精度.仿真实验结果表明：与原算法相比,改进算法能够降低累积误差带来影响,定位精度明显提高.

无线传感器网络；自身定位算法；DV-HOP算法；异方差；最小二乘原理

无线传感器网络（wireless sensor network,WSN）通过部署在目标区域的大量传感器节点,将采集到的数据在全网中进行传输,实现对目标的监测.WSN在未来有极广泛的应用前景,而在其各种应用中,传感器节点所捕捉到的数据必须与位置信息相结合才能加以采用.因此节点定位是WSN正常运行的首要工作,同时也是当前无线传感器研究的重点,有许多问题还有待于解决.

传感器节点的具有体积小、能耗低、自身资源有限等特点,传统的GPS等定位方法并不适合传感器网络,比较现实的做法是将网络中的若干传感器配备GPS接收器或由人工配制位置信息,将这样的传感器节点作为参考节点,而没有位置信息的节点为未知节点.传感器网络定位问题所要解决的就是未知节点如何根据参考节点的位置进行自我定位.

WSN定位算法的发展到目前可分为两类：基于测距的（Range-based）和非基于测距的（Range-free）.基于测距的算法主要依据信号接收的强度和时间、信号到达的时间差和角度等信息测量相邻节点距离,优点是定位精度较高,缺点是成本和能耗开销大,规模较大的传感器网络不适合这种算法.非基于测距的算法主要是根据网络的连通性进行定位,由于不需要对距离进行测量,所以成本和功耗相对较低,且对硬件支持等要求较低,因此这类定位方案近年来发展较快.例如：质心法、APIT、Amorphous、LSBA等[1-3].而其中DV-HOP（Distance Vector-HOP）节点定位算法[4-5]由于具有定位精度相对较高、算法简单、对参考节点比例要求较低等特点,受到较多关注.本文着眼于对DV-HOP算法进行研究,加以改进以进一步降低算法误差.

1 DV-HOP算法及误差分析

DV-HOP算法是为了避免节点之间直接测量距离提出来的.它的基本思想是用网络中节点之间的平均每跳距离和节点之间的跳数乘积表示待定位节点之间的距离,然后采用三角定位的方法获取节点的定位信息.DV-HOP定位算法大体分为3步：

（1）节点间使用距离矢量交换协议交换位置信息,使未知节点获得与参考节点之间距离值,该距离值以跳数表示.

（2）在获得其他参考节点位置（Xj,Yj）和相隔跳数后,各参考节点（Xi,Yi）利用所收集的信息按式（1）计算平均每跳距离

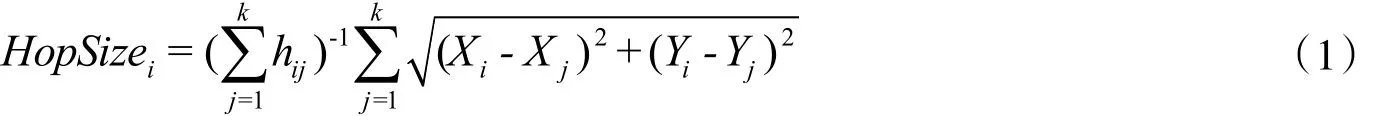
（3）在未知节点收集到与3个或更多参考节点之间的距离信息时,就可以用最小二乘法来确定自身的位置信息.

假设未知节点所得到参考节点的坐标分别是（x1,y1）,（x2,y2）,…,（xn,yn）,且它们到未知节点D的距离以d1,d2,…,dn表示,设未知节点D的坐标是（x,y）,则可得到

在式（2）中,由第一个方程开始分别减去最后一个方程,可得

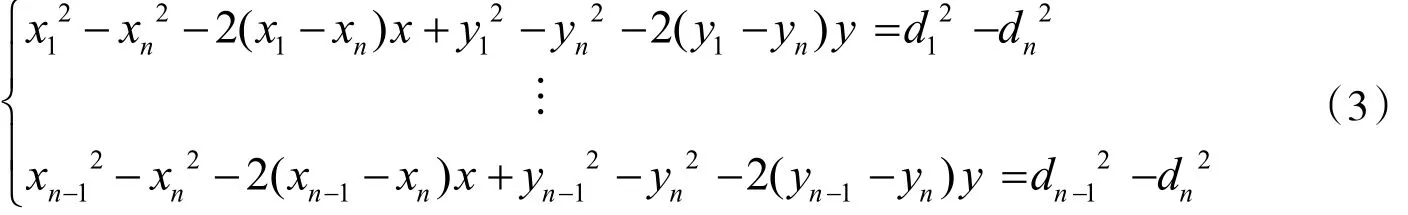
式（3）用线性方程表示为

式（4）中

最后使用最小均方差估计方法,得到未知节点的坐标

假设参考节点的初始坐标是由GPS测量得到的.由于存在多径干扰[6],测到的参考节点坐标有误差,而以这些节点位置数据作为待求节点的约束条件,导致求出的新节点位置也存在数据误差.这些误差在以后递推定位计算中不断传播与积累,使得到的节点位置数据存在较大误差.从数学上讲,DV-HOP算法定位计算是基于普通最小二乘法（Ordinary Least Squares,简记OLS）.普通最小二乘法的基本原则是：最优拟合直线应该使各点到直线的距离的和最小,也可表述为距离的平方和最小,即Ax=b+△b,其中,△b是测量误差.而事实上,与定位机制相关的矩阵A是由参考节点位置信息决定的,因而与不断积累的定位误差有关联的.目前已对DV-HOP算法提出多种改进方法,其中主要有：提高算法的平均跳距估计精度[7-10]；改进最后一步的定位计算方法[11]；与其他定位算法相结合等[12].

在DV-HOP算法中,节点位置由式（5）用标准最小二乘方法求得.最小二乘法是基于测量均方误差最小的算法,在对应的测量方程Ax=b+△b中,没有考虑到A也是存在误差的.在确定节点的过程中,依据的新参考节点（xi,yi）是以前计算的节点（i=1,2,…,N）,其本身就有误差.当考虑到这一误差时,测量方程应为（A+△A）x=b+△b.也就是说,用最小二乘基于均方差假设得到的节点位置信息不是最优的.针对这个问题,我们提出用异方差存在假设来替换OLS的均方差假设,并对异方差进行消除的方法,以下给出求解节点位置的理论根据与仿真结果.

2 结合异方差消除原理的DV-HOP定位算法

2.1 产生异方差的原因

由于在线性回归模型中采用最小二乘法估计模型中的参数,根据其假设条件,随机误差项具有以下性质：

（1）在一元线性回归模型y=a+bx+ε中,其误差项ε属于位置偏差,即绝对误差.根据一元线性回归模型的假设条件,则ε～N（0,σ2）.

（2）在多元线性回归模型y=b0+b1x1+b2x2+...+bnxn+ε中,随机误差项属于位置偏差,按照多元线性回归模型假设条件,满足ε～N（0,σ2）.以上都是满足同方差假定条件,在这种情况下的最小二乘法（OLS）估计称为最佳线性无偏估计[13]（Best Linear Unbiased Estimators,简记BLUE）.

而对于线性回归模型

若D（εi）=σ2≠常数,则表明模型显现出异方差性.在这种情况下,OLS估计不再是最佳线性无偏估计BLUE,即不满足最小方差性质.由于无法准确估计系数的标准差,则检验[14]可靠性减小,导致模型估计误差的加大.在利用截面数据建立模型时,则会产生异方差.而导致模型系数估计产生误差的原因一般就是由于在建立模型时遗漏了影响增大的因素.

2.2 异方差的消除

加权最小二乘法（Weighted Least Squares,简记WLS）[13]和模型变化法是消除异方差的常用方法,这里,选用WLS.WLS的思想是在同方差模型假定下,每个残差ei[13]对总体回归直线的偏离程度大致相同,权数都赋为1,这时OLS估计满足BLUE估计；当模型存在异方差性时,每个ei对总体回归直线的偏离程度不同,对于σi2较大,即偏离程度较大的ei,样本点可信度随之降低,就对其赋予较小的权数,而对σi2较小,说明偏离程度较小的ei,样本点的可信度较大,则随之赋予较大的权数,使模型估计时残差的加权平方和最小.

设一元回归模型y=a+bxi+εi若D（εi）=σ2,两边同除以σi得到消除了模型的异方差性.这时可以利用最小二乘法（OLS）估计模型.使得

提出的改进算法如下：首先根据参考节点位置信息对未知节点的距离进行估算,估算出未知节点到邻近3个或者3个以上参考节点的距离值,然后用加权最小二乘法来消除式（5）中出现的异方差,最终得到未知节点的坐标信息.

3 改进算法的仿真

用仿真的方法比较使用普通最小二乘法OLS和使用加权最小二乘测量法WLS经过异方差消除改进后的DV-HOP定位算法的性能,证明改进算法的有效性.仿真工具采用Matlab7.0,使用平均定位误差（Estimation Error）来作为算法评价的标准.平均定位误差是所有节点的估测位置和真实位置之间相差的平均距离,在本次实验中用节点的通信距离将其归一化.实验中传感器网络节点分布在200 m×200 m的区域内,节点最大通信距离为50 m,干扰噪声服从高斯分布,所有实验数据都是在独立运行100次之后得到的.

3.1 变化误差率

讨论出现明显误差的参考节点的比例变化对定位误差的影响.实验参数设置如下：传感器节点总数为200,参考节点个数为30,标准差为30 m,存在显著误差的参考节点信息比例从30%增加到100%.比较结果如图1.

由图1可以看出,在参考节点误差率低于60%的情况下,两种算法的定位误差相差不大,但在误差率继续增加时,原始算法的定位误差迅速增加,而改进后算法则对于误差信息干扰的抑制较为明显,始终将位置信息误差带来的影响控制在较低的范围.说明在参考节点误差率较高的情况下,改进后算法的优势更加显著.

3.2 变化标准差

标准差的变化反映了参考节点位置信息所出现误差的变化范围.本节讨论标准差从20 m增加到100 m的过程中对DV-HOP算法定位精度的影响.实验参数设置如下：参考节点个数为30,误差率为50%.比较结果见图2.

从图2来看,在标准差高于大约25 m以后,改进后的算法的定位精度始终高于原始算法,随着标准差的增加,原始算法的定位误差也明显继续加大,而改进后算法的定位误差并没有显著增加,在标准差越高时,改进算法的优势越为明显.

3.3 变化参考节点数目

讨论参考节点总数从20增加到100的情况下对定位算法性能的影响.实验参数设置如下：参考节点误差率为50%,标准差为30 m.比较结果见图3.

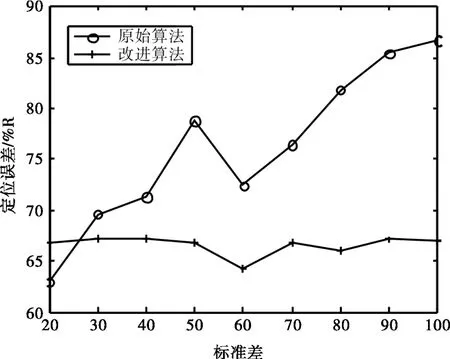
图2 标准差对定位算法性能的影响Fig.2 Change of standard deviation to positioning accuracy

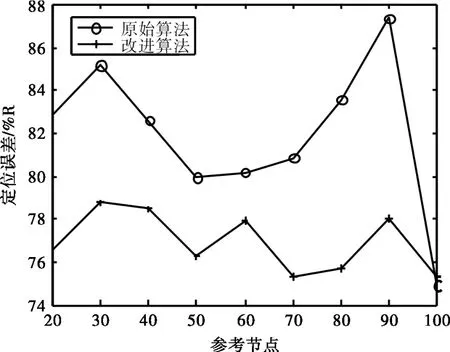
图3 参考节点数对定位算法性能的影响Fig.3 Change of reference number to positioning accuracy

一般情况下参考节点数目越多定位误差应该越小,但是从图3来看,在参考节点数目逐渐增加的情况下,两种算法的定位误差变化出现起伏.这是由于误差率不变的情况下,参考节点数量的增加在带来更多位置信息的同时也会导致带来更多误差信息.但改进算法的定位误差始终低于原始算法,并且定位误差的波动相对于原始算法并不明显,表明在使用异方差消除算法后改进算法能明显减少参考节点位置信息误差带来的影响.

4 小结

本文对DV-HOP定位算法产生误差的原因进行了理论分析,针对基于OLS原理的DV-HOP算法的缺点,提出了基于异方差假设,采用基于异方差消除的WLS原理改进的DV-HOP算法.仿真实验表明,改进算法较明显提高了DV-HOP算法的定位精度.改进方案具有良好的扩展性,未来将研究将其应用到其它基于最小二乘原理的定位算法之后的使用效果.

[1]Bulusu N,Heidemann J,Estrin D.GPS-less low cost outdoor localization for very small devices[J].IEEE Personal Communications, 2000,7（5）：28-34.

[2]He T,Huang C.Range-Free localization schemes for large scale sensor networks[C].In：Proc 9th Annual Int’l Conf on Mobile Computing and Networking,San Diego：ACM Press,2003：81-95.

[3]Li X,Hua B,Guo Y.Link state based annulus localization algorithm for wireless sensor networks[C].Proceedings of the International Conference on Communications and Networking,Shanghai：ICST,2007：298-303.

[4]Niculescu D,Nath B.DV based positioning in Ad hoc Networks[J].Journal of Telecommunication Systems,2003,22（1/4）：267-280.

[5]张震,闫连山,刘江涛,等.基于DV-Hop的无线传感器网络定位算法研究[J].传感技术学报,2011,24（10）：1469-1472.

[6]吴顺君,梅晓春.雷达信号处理和数据处理技术[M].北京：电子工业出版社,2008：146-149.

[7]林金朝,陈晓冰,刘海波.基于平均跳距修正的无线传感器网络节点迭代定位算法[J].通信学报,2009,30（10）：107-113.

[8]张佳,吴延海,石峰,等.基于DV-HOP的无线传感器网络定位算法[J].计算机应用,2010,30（2）：323-326.

[9]刘少飞,赵清华,王华奎.基于平均跳距估计和位置修正的DV-HOP定位算法[J].传感技术学报,2009,22（8）：1154-1158.

[10]丁江鹏,陈曙.一种基于跳数比的无线传感器网络定位算法[J].传感技术学报,2009,22（12）：1823～1827.

[11]王书锋,侯义斌,黄樟钦,等.无线感知网络最小二乘法定位算法的误差分析与优化[J].系统仿真学报,2009,21（19）：621l-6215.

[12]胡斌,李方敏,刘新华.基于RSSI量化模型的定位算法研究[J].武汉理工大学学报,2009,31（23）：92-95.

[13]王军.回归模型异方差性分析[J].科技和产业,2008,8（1）：61-63.

[14]刘明.基于一元线性回归模型异方差对加权最小二乘法的考察[J].统计与决策,2012（19）：11-14.

（责任编辑：卢奇）

Study of improving location accuracy based on DV-HOP algorithm

Zhang Jia1,Liu Yanchang1,Wang Xianfang2
（1.Henan Institute of Science and Technology,Xinxiang 453003,China；2.College of Computer and Information Engineering,Henan Normal University,Xinxiang 453007,China）

Wireless sensor networks have been wildly used in target tracking,environmental monitoring and space exploration,etc.One of its key supporting technologies is node localization.The DV-HOP algorithm is taken as the research object.To break the algorithm’s calculation application restrictions,the heteroscedasticity elimination principle is adopted when obtaining node location information through the Least Squares principle.This method is applied to remove distinct errors emerging when referring to the node location information and improve the positioning accuracy of unknown nodes.The simulation experiment results demonstrate that the improved algorithm can reduce the affects which the accumulation error brings about and improves the positioning accuracy compared with the original algorithm significantly.

wireless sensor network；self-location algorithm；DV-HOP algorithm；heteroscedasticity；least squares principle

TP393

A

1008-7516（2013）05-0058-05

10.3969/j.issn.1008-7516.2013.05.014

2013-07-11

国家自然科学基金项目（61173071）

张佳（1979-）,男,河南新乡人,硕士,助教.主要从事无线传感器网络研究.