城市固体废弃物(MSW)的压缩规律和沉降模型

孙 龙,施建勇,胡兴昊

(河海大学 岩土工程研究所,江苏 南京 210098)

0 前 言

城市固体废弃物成分复杂,且组分差异性很大;其中,纸、塑料、木材、厨余、渣土是主要成分,MSW(municipal solid waste)降解规律复杂、孔隙比大,主次压缩难以准确区分,压缩与降解对沉降的耦合作用使得MSW的沉降预测尤为困难。早期,Sowers[1]提出了一组分别计算新填MSW的主固结沉降量和次固结沉降量的半对数沉降模型,也有人提出将主次固结归一计算总沉降。Gibson和Lo[2]提出了一种把主、次固结沉降归入一个函数式的指数型沉降模型;Hoe等[3]在对数模型和指数模型的基础之上,提出了双曲线模型。Park和Lee[4]认为降解引起的沉降过程可以用一阶动力学函数方程来表达,沉降中考虑了生化降解作用。国内对于垃圾土沉降的影响研究起步较晚,但发展较快。钱学德和郭志平[5]对MSW的工程性质进行了长期的研究,确定了工程基本力学参数取值范围。张振营和陈云敏[6]通过对沉降变形机理分析,把沉降分为压缩沉降和降解压缩沉降两部分,提出了垃圾土沉降的相变计算方法;朱青山等[7]根据室内试验,认为沉降与时间成正比提出了次固结沉降模型;廖智强[8]认为可以用KELVIN模型来模拟填埋场次压缩沉降,并通过室内蠕变试验求得了KELVIN模型的参数,柯翰[9]根据上海老港封顶系统的部分实测沉降数据拟合了3种沉降计算模型的参数,模拟分析了分层堆填条件下填埋场的堆填及沉降过程。

现有的研究成果,建立了预测降解压缩的计算方法。但对于压缩特性中的主次压缩作用尚无法区分,压力对垃圾土次压缩的影响尚无研究报道,次压缩与降解沉降简单归入长期沉降。

本文针对垃圾土明显的次压缩特性,考虑降解、主次压缩分离、降解与主次压缩耦合作用,修正了预测垃圾土沉降的模型,通过试验结果对沉降模型进行了验证。

1 基本理论

现有的研究是将主次压缩对沉降的影响根据主固结时间分段考虑。而在实际情况中,主次压缩是在加载瞬间同时出现的。为了解决这一问题,本文引用殷建华[10]的次压缩模型,该模型将次压缩的计算时间提前到初始加载时刻。

次压缩 Δ e2计算式为:

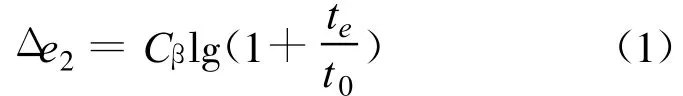
式中:Δ e2是次压缩孔隙比变化值;cβ是次压缩系数;te是等效时间,即蠕变开始的时间,从有效应力施加开始计算;t0是修正参数并非是主固结完成时间。

可以看到,在te为0的时候,等式右边是有意义的,即等于0。这样,从应力的施加初期就能明确次压缩的大小;而不用像以往,将主固结期间或是前24 h的次压缩归结为主压缩。

主压缩试验结果的e-lgp是线性关系。

主压缩 Δ e1计算式为:

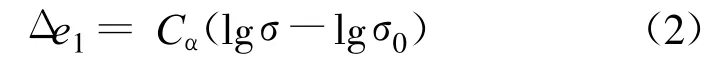
式中:Δ e1是主压缩孔隙比变化值;cα是主压缩系数,即 e-lgp直线的斜率;σ是有效应力;σ0是前期固结应力。

总压缩 Δ e:

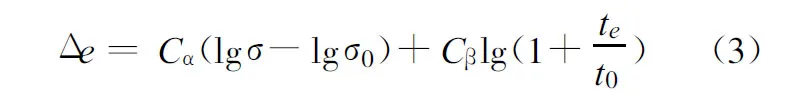
图1是e-t坐标轴中实际主次压缩曲线和次压缩拟合曲线比较示意图。

式(1)是计算次压缩大小的模型,根据图1中t1之后的次压缩曲线可求得次压缩未开始时刻的孔隙比,也即无次压缩影响的孔隙比。

图1中,e0是根据主固结完成后的次压缩曲线,用式(1)拟合求得,也即压力p0下无次压缩影响的孔隙比。t1是实际主固结完成时间,此时试样的孔隙比是e1;按照传统主次压缩计算理论,压力p0作用下的孔隙比就是e1;则压力p0下考虑次压缩影响和不考虑次压缩影响的差别就是e0-e1;由此可见,利用主固结之后的次压缩曲线拟合全段次压缩曲线,反推求得消除次压缩影响的孔隙比是十分必要的。否则,总是将主固结时间内的次压缩归结为主压缩,会引起相当的误差。图1中纵坐标e为孔隙比,横坐标t为时间。

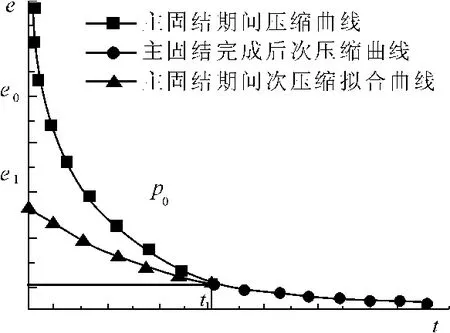
图1 次压缩拟合曲线示意图

将次压缩开始时间从理论上提前到荷载加载初期,可以明确主次压缩分别对沉降的贡献大小。

图2是多级加载的示意图。

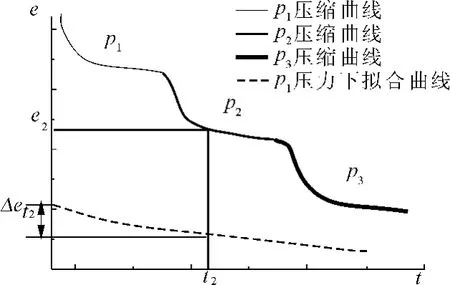
图2 多级加载示意图

在多级加载时,由于每个试样的次压缩系数都是在12.5 kPa下测得的,这样在进行各个试样的次压缩系数比较时,可以不考虑压力对次压缩系数的影响。

2 压力对主次压缩的影响

2.1 压力试验

2.1.1 试验装置与试验条件

试验采用常规重型固结仪,采用人工配置垃圾土。试样经过粉碎,粒径均小于5mm,试样体积为60cm3,高 2cm。初始含水率为100%,干密度为0.372 g/cm3,初始孔隙比为4。各个试样除加载压力不一样外,其他条件控制一致。由于垃圾土试样颗粒较大,属于散粒材料,因而在试验中制样比较困难;另一方面,材料的回弹性比较大,这增加了制样的难度。故采取直接向固结仪中填样的方法,填样的质量根据初始孔隙比和含水率确定。装样完成之后即加载,从加载初始时刻开始记时,采用人工读数。

压缩试验采用向垃圾土中加醋降低垃圾土pH的方法抑制降解[11],控制降解对压缩的影响。垃圾土的初始含水率较低,试样过程中始终用湿布覆盖,减少水分蒸发的影响。

2.1.2 试验结果

试验荷载从12.5 kPa～1600 kPa共分10级,试验得到的e～t曲线如图3所示。

图3中可以看出,各级荷载下次压缩曲线的切线斜率相差不大,有相同的趋势。根据试验结果用式(1)进行拟合求得次压缩系数cβ。

[13]胡志丁、曹原、刘玉立、葛岳静：《我国政治地理学研究的新发展：地缘环境探索》，《人文地理》2013年第5期。

2.2 压力对次压缩的影响

总体来说次压缩系数受压力的影响不是很明显,当用对数时间坐标时,其取值范围为0.035～0.049,并且与对数压力基本呈线性关系。图4是次压缩系数与对数压力的关系图。12.5 kPa和1600 kPa次压缩系数差别大约在28%左右。

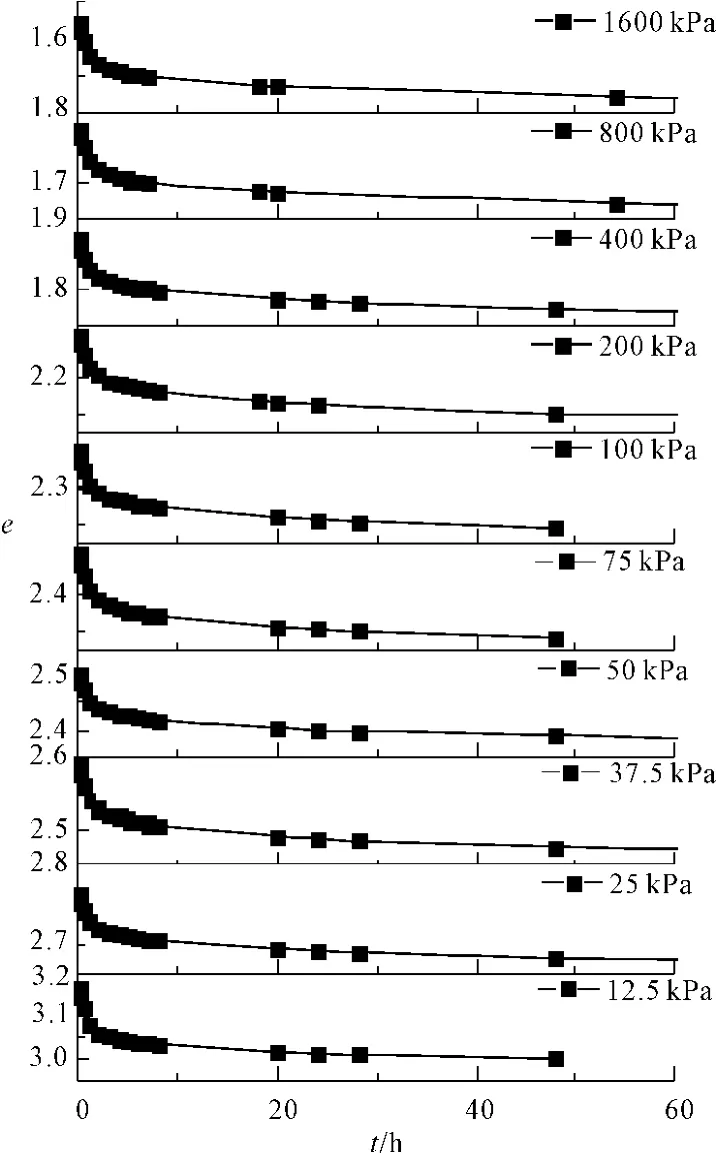
图3 各级荷载下 e-t曲线

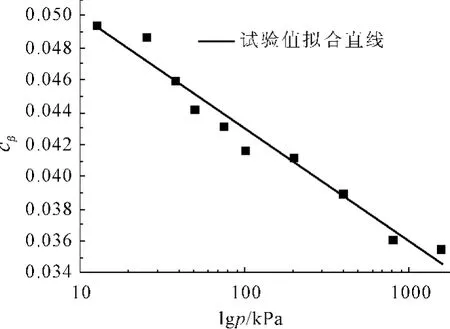
图4 次压缩系数-对数压力关系图

根据图1理论计算得到图3中各级荷载下的无次压缩影响的孔隙比e0,见表1所示。

表1 各级荷载下的修正孔隙比

2.3 压力对主压缩的影响

2.3.1 压力与孔隙比关系

将每一级荷载(12.5 kPa～1600 kPa)下的压缩曲线(如图3所示)用图1所示方法进行拟合求得修正后各级荷载下的孔隙比e0,见表1。作e-lgp关系图,见图5。该线性关系的斜率即为主压缩系数cα。可以看到孔隙比和对数应力基本呈线性关系,并无传统土力学理论中所出现的前期固结应力拐点。

2.3.2 压缩试验中主固结时间的确定

对于常规土样,是以24 h或者每小时沉降量不大于0.005mm作为主固结结束时间(压缩稳定标准);垃圾土渗透系数远比土体大,其主固结结束时间理应比普通土体小。对于垃圾土来说,相对于普通土体变形具有量级的变化,如果按照普通土体的变形标准,在48 h时后变形仍不能达到稳定,对于试验时间条件来说难以接受。所以探索垃圾土的主固结稳定时间就显得很有必要。

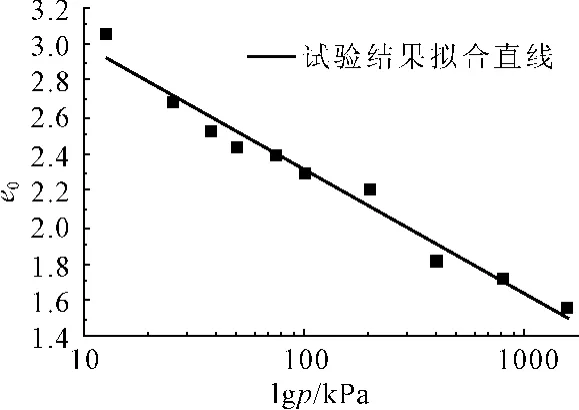
图5 孔隙比-对数压力关系图

图6是各级荷载下取不同时间作为主固结完成时间,求得的次压缩系数与选定的主固结完成时间关系图。

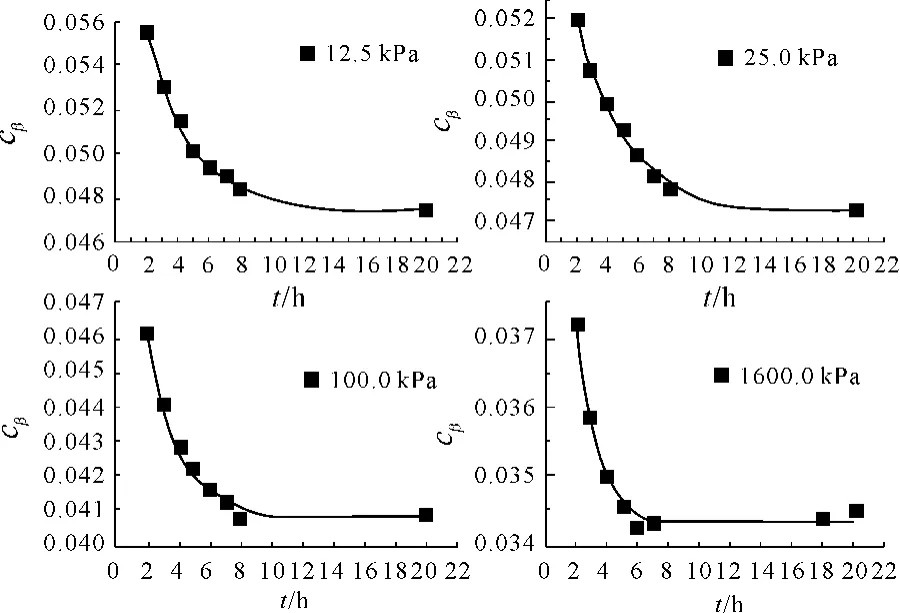
图6 次压缩系数-选定主固结结束时间关系图

从图6中各级荷载下的曲线图可以看出,在6 h～8 h左右,曲线出现明显的拐点;8 h之后,取各个时间作为主固结结束时间对次压缩系数的影响已经不大;在压力较小时,拐点在7 h～8 h,在压力较大时,拐点还不到7 h,在6 h～7 h左右。在压力较小时,8 h之后,次压缩系数随时间增大有微弱减小;而在压力较大时,次压缩系数随时间增大有微弱增大。故在垃圾土压缩试验中,取8 h作为主固结结束时间。

2.3.3 主固结结束时间的选定对修正后孔隙比 e0的影响

在图1中,t1是主固结完成时间,根据这个主固结完成时间,可以在图1中拟合得到一个修正后的孔隙比e0。但在实际情况中,无法准确的确定主固结完成时间,故需要知道设定的不同的主固结完成时间对修正后孔隙比e0的影响。对图3中各级荷载下的压缩曲线分别取不同的主固结完成时间,用图1的方法进行拟合。以设定的主固结完成时间t1为横坐标,修正后孔隙比e0为纵坐标,作出各级荷载下的关系图,见图7。

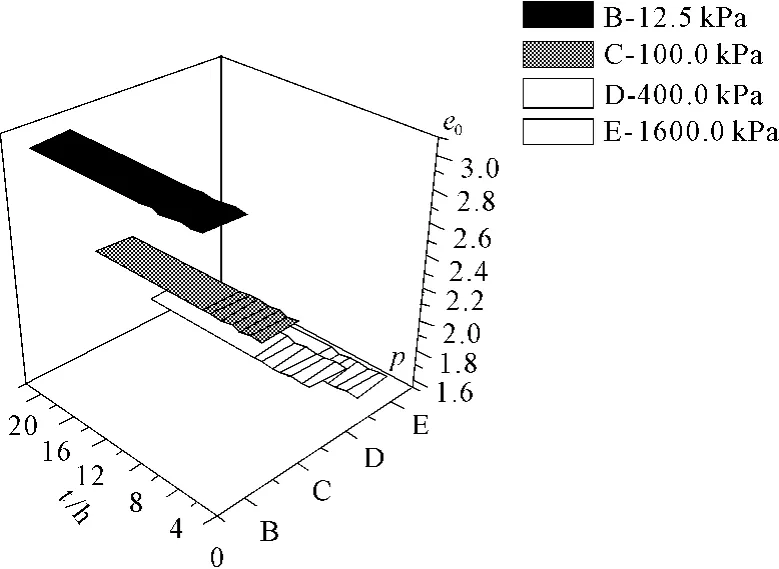
图7 修正后孔隙比与选定的主固结结束时间关系图

从图7中可以看出,各级荷载下的曲线几乎水平。说明不同主固结完成时间的选定对于该级荷载下修正后的孔隙比 e0影响很小。随着选定主固结完成时间的增大,修正后孔隙比在低压下有微弱的降低,在高压下有微弱的增大。

2.4 比重试验

采用比重瓶法,由于垃圾土中含有大量有机质,所以采用酒精作为溶剂,在一个大气压下抽真空4 h以上,图8是九组比重试验结果。

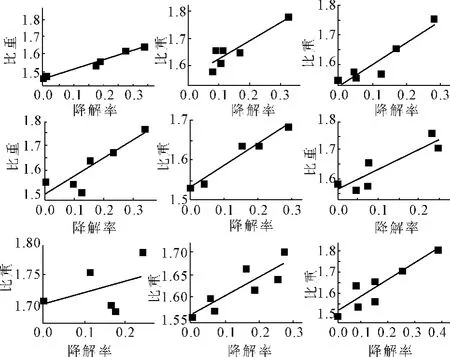
图8 比重-降解率关系图

根据图8结果可知,比重随着降解率的增大而增大。垃圾土干物质(固体)由有机物与无机物组成,无机物的比重一般是大于有机物的,所以有机物越少,混合物比重越大。

由于直线拟合效果较好,且应用方便,故用线性关系来描述比重与降解率之间的关系。

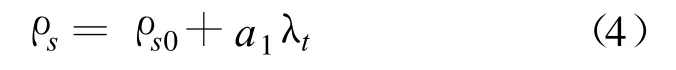
式中:ρs为最终比重 ;ρs0为初始比重;λt为降解率;a1为直线斜率。

3 沉降模型

本文沉降模型的推导是在张振营[6]模型的基础上,引用刘晓东[11]降解模型及上述主次压缩模型加以改进而得。

模型基本假定:

(1)MSW中干物质及水本身是不可压缩的。

(2)沉降是在一维进行的,不考虑侧向变形。

(3)当降解率相同时,在相同压力下孔隙比相同,与受力体积无关。

(4)降解引起两方面的沉降;一方面是骨架减少,另一方面是降解引起的主压缩系数的增大。

(5)不考虑降解对次压缩的影响。

图9是降解压缩前后试样对比示意图。其中,h0、h是压缩前后试样的高度,vv0、mv0是初始孔隙体积和质量,vs0、ms0是初始固体体积和质量;vv、mv是降解后某一时间孔隙体积和质量,vs、ms是降解后某一时间的固体体积和质量,λt代表某一时间的质量降解率。

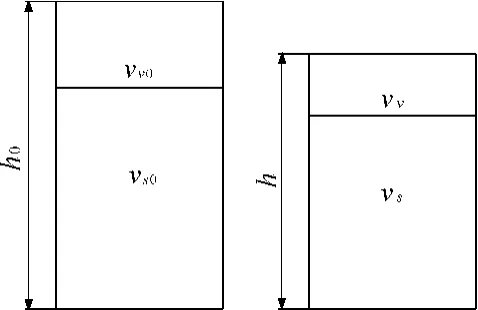
图9 压缩示意图

沉降 :Δ h=h0-h据此可得[6]:

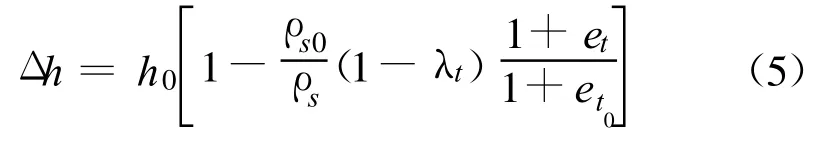
式中:ρs0是初始比重;ρs是t时刻比重;λt是降解率;et0是初始孔隙比;et是t时刻孔隙比。

降解率与时间的关系以及参数确定方法具体可见文献[11]:

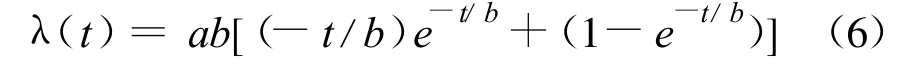
式中:a、b降解参数。

将式(4)代入式(5)可得:

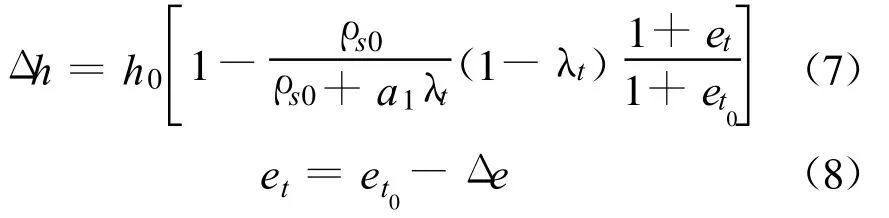
降解会使土体骨架软化,直接反映在降解模型中就是主压缩指数的变大,在文献[12]中,主压缩指数与降解率呈线性关系

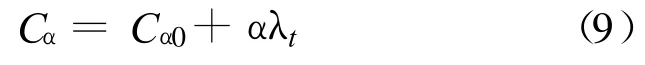
式中:Cα0是未降解时的主压缩指数;Cα是降解之后的主压缩指数;α是主压缩指数-降解率直线斜率。将式(9)代入式(3)可得:

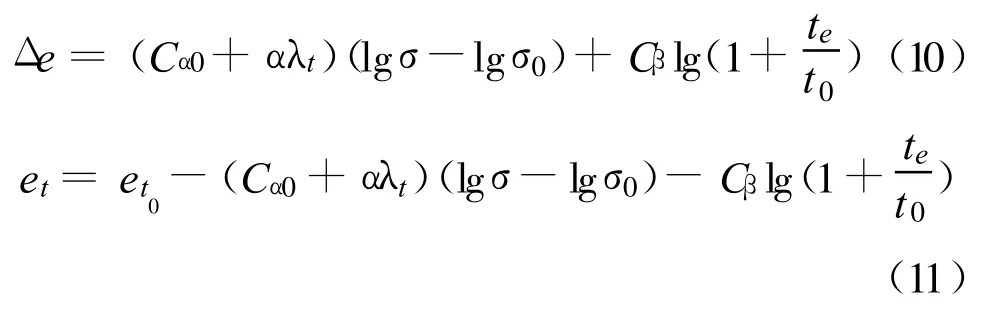
将式(11)代入式(7)可得:

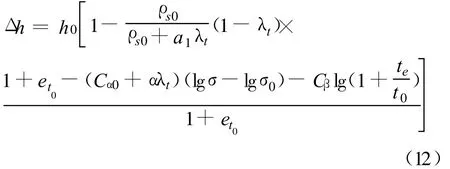
如不考虑比重随降解率的变化,则沉降模型可简化为:

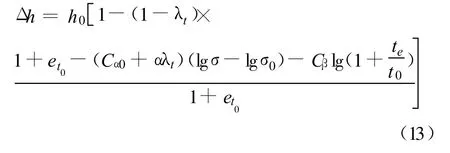
4 室内试验

结合文献[13]的室内沉降试验,运用沉降模型进行计算,验证本文模型的合理性、适用性。

文献[13]在2004-07-13到 2005-01-29期间进行了垃圾土人工试样沉降观测试验,试验仪器尺寸为46.3cm×28.5cm,试验控制条件如下:

初始干密度:0.171 g/cm3,含水率接近饱和;

外载:0.62 kPa,不加水,收集淋滤液;

初始孔隙比:7.1

根据sowers的建议:Cβ=(0.03～0.09)×e0

考虑到有侧壁摩擦力的影响取小值:0.2

主压缩参数根据试验取值:

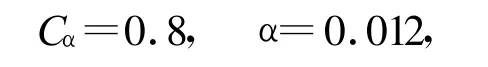
有机质的降解参数:a=0.0025,b=36

实测数据与理论模型计算对比如图10所示。

由试验与计算对比结果可以看出,模型计算值同试验数据吻合的很好,验证了本文模型的合理性。初始阶段存在一定的偏差(小于5%),这主要是由于碗状垃圾样和桶状垃圾样在降解环境方面存在较大的差异。

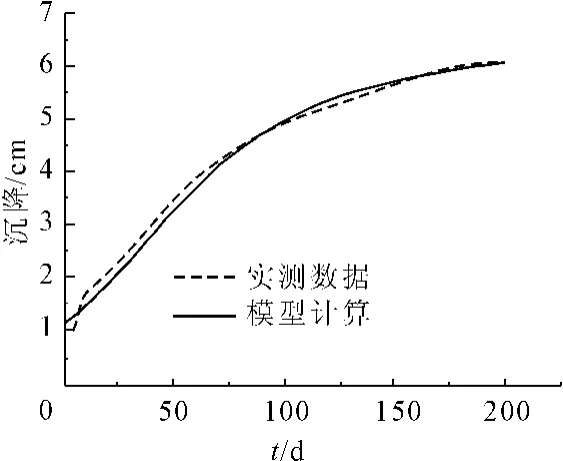
图10 文献[13]试验计算模型与实测数据对比图

5 结 论

(1)垃圾土的次压缩与压力关系不大,在压力增大的时候,次压缩系数会有一定的减小,并与对数压力呈线性关系。

(2)将次压缩计算时间提前到加载时刻,从填埋初期就能明确主次压缩对沉降各自的贡献,为更准确地预测填埋场沉降打下理论基础。

(3)主固结结束时间与压力大小有一定的关系。在垃圾土压缩试验中,主固结结束时间比常规土要小的多。

(4)在垃圾土沉降计算中,考虑主压缩、次压缩、降解三者的耦合作用,建立了垃圾土沉降预测模型,并通过室内试验验证了其合理性。

[1]Sowers SK.Settlement of waste disposal fills[C]//Proc.8th Int.conf.Soil Mech.and Found.Engrg.,Moscow,1973:207-210.

[2]Gibson R E,Lo K Y.A theory of consolidation of soils exhibiting secondary compression[M].Scandinavia:Acta Polytech Scand,1961.

[3]Hoel L,Dov L,YoshiyukiM,et al.Estimation of municipal solid waste landfill settlement[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1998,124(1):21-28.

[4]Park H I,Lee S R.Long-term settlement behavior of MSW landfills with various fill ages[J].Waste Management and Research,2002,20(3):259-268.

[5]钱学德,郭志平.城市固体废弃物(MSW)的工程性质[J].岩土工程学报,1998,29(5):1-6.

[6]张振营,陈云敏.城市垃圾填埋场沉降模型的研究[J].浙江大学学报(工学版),2004,38(9):1162-1165.

[7]朱青山,赵由才,徐迪民.垃圾填埋场中垃圾降解与稳定化模型试验[J].同济大学学报,1996,24(5):596-600.

[8]廖智强.卫生填埋降解试验研究及沉降机理分析[D].南京:河海大学,2006.

[9]柯 瀚,王耀商,陈云敏,等.分层堆填条件下填埋场沉降计算及实例分析[J].岩土工程学报,2011,33(7):1029-1035.

[10]殷建华.从本构模型研究到试验和光纤监测技术研发[J].岩土工程学报,2011,33(1):1-15.

[11]刘晓东.考虑生化降解的城市固体废弃物(MSW)力-液-气耦合沉降模型及试验研究[D].南京:河海大学,2012.

[12]胡亚东.有机质降解规律及对垃圾土变形影响的研究[D].南京:河海大学,2006.

[13]方云飞.城市生活垃圾(MSW)有机物降解和变形规律研究[D].南京:河海大学,2005.