基于计算力矩法的永磁球形电动机轨迹跟踪控制
李洪凤,宋振辉,郭 辰,李 斌
(1. 天津大学电气与自动化工程学院,天津 300072;2. 华能新能源股份有限公司,北京 100036)
基于计算力矩法的永磁球形电动机轨迹跟踪控制
李洪凤1,宋振辉1,郭 辰2,李 斌1
(1. 天津大学电气与自动化工程学院,天津 300072;2. 华能新能源股份有限公司,北京 100036)
永磁球形电动机动力学系统是一个多变量、非线性、强耦合系统.外部扰动、参数估计误差以及模型的近似均会影响系统的控制效果.为了获得良好的静态和动态性能,改善轨迹跟踪性能,提出了一种基于计算力矩法的永磁球形电动机轨迹跟踪控制策略.仿真结果表明,此方法可有效地削弱各轴向间非线性交叉耦合的影响,对外部扰动和模型误差具有良好的鲁棒性,可实现理想的轨迹跟踪控制效果.
永磁球形电动机;动力学模型;轨迹跟踪;计算力矩法
做多自由度运动的传统精密装置,如机器人关节、机械手关节等,往往需要多台单自由度驱动元件以及复杂的机械传动装置来实现.这导致系统复杂、驱动元件之间协调性差、响应迟缓、精度不够、效率低等一系列问题.能够完成多自由度运动的球形电动机可以大大简化机构的复杂程度,缩小机构体积,提高定位精度和响应速度,成为国内外学者的研究热点.
国内外学者关于球形电动机研究取得了一定的成果,当前所研究的球形电动机主要包括变磁阻型球形电动机[1]、感应型球形电动机[2]、双馈型球形电动机[3]、永磁步进球形电动机[4]和永磁球形电动机(permanent magnet spherical motor,PMSM)[5-7],其中Halbach阵列永磁球形电动机有效地改善了电机的电磁场分布,提高了电机性能,具有结构简单、体积小、重量轻、可靠性高、低成本和便于控制等独特优点[8-10].
在球形电动机的控制方面,美国佐治亚理工大学研究者提出了一种解耦控制法来实现对球形步进电机的旋转运动控制,并且以其动态模型为基础控制转子倾角[11].德国亚琛工业大学研究者针对永磁球形电动机提出了一种变极距转矩控制策略[6].美国霍普金斯大学研究者设计开发了一种新型永磁球形步进电动机,并对该球形电动机的定转子空间位置排列进行了深入探讨,提出了一种基于二元数学模型的球面运动编码器,用于对转子位置进行检测[4,12].合肥工业大学研究者提出了一种基于加权无向图的永磁球形步进电机运动控制方法[13].华中科技大学研究者针对球形双馈电动机,提出了该电动机的力学模型和电磁模型,以及一种基于前馈和矢量控制的控制策略[14].
在球形电动机轨迹跟踪控制中,传统PD控制算法作为一种不基于模型的控制算法,其轨迹跟踪误差较大;直接前馈补偿法的实现较简单,具有较好的控制效果,但由于其耦合项的构造依靠对输出量的在线采集,因此在线计算量较大[14].文献[15]提出并采用计算力矩法实现了对永磁球形电动机动态解耦控制,但此方法基于简化的动力学模型,与实际系统存在较大的误差.笔者建立了永磁球形电动机的完整动力学模型,并采用计算力矩法来实现其轨迹跟踪控制,克服了简化模型带来的控制系统不准确性;同时,对系统的鲁棒性进行了分析,扩展了运动控制的研究思路.
1 永磁球形电动机结构及工作原理
永磁球形电动机由半壳型定子和球形转子构成,基本结构如图1所示.内部转子由嵌入外部定子球壳的静压油轴承支撑以实现高转矩和低摩擦损耗,其表面由N、S极交替排列的钕铁硼永磁体粘贴而成,对每块永磁体采用平行充磁.在定子壳上按一定规律放置集中绕组线圈.转子输出轴上装有法兰,以传递电机产生的电磁力和电磁转矩.
永磁球形电动机的电磁转矩由定子通电线圈和转子永磁体之间磁场的相互作用产生.采用一定的次序对定子绕组线圈进行通电,产生足够大的转矩,便能驱动转子旋转.当给沿赤道上分布的定子线圈通电时,转子会产生自转运动;当给同一经度上的定子线圈通电时,转子会产生俯仰或偏航运动;但限于自身机械结构和制造工艺的限制,对于后2种运动形式,只能在一定角度范围内实现.这样通过改变定子线圈的通电策略,当在各方向均产生足够大的转矩时,就使电机输出轴实现自转、偏航、俯仰3个自由度的运动,从而使联结在电机转子上的负载获得3自由度的运动.
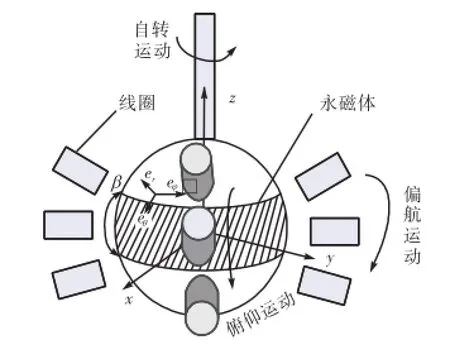
图1 永磁球形电动机结构Fig.1 Structure of PMSM
2 永磁球形电动机动力学模型
永磁球形电动机动力学模型代表的是施加于其上的转矩与未知变量之间的关系,采用拉格朗日法对永磁球形电动机动力学模型进行推导,由拉格朗日方程可得
式中:Ε=Κ-Ρ,K为质点系动能,P为质点系位能;θj为质点系中第j个广义坐标;Qj为广义坐标θj对应的广义力.
对于永磁球形电动机,其质点系是一个单独的转子球体,并且系统位能为零,则Ε=Κ.此时k=3,广义坐标θ1=α,θ2=β,θ3=γ;广义力Q1=τα-τfα,Q2= τα-τfβ,Q3=τγ-τfγ,其中τfα、τfβ和τfγ表示转子在3个轴向上的负载转矩与摩擦转矩之和.在坐标系xyz中,永磁球形电动机转子球体的动能表达式为
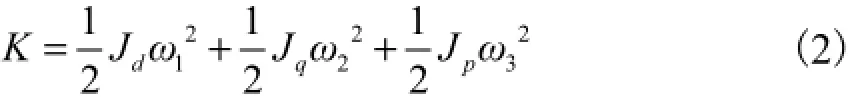
式中:Jd、Jq和Jp分别为永磁球形电动机转子在dqp坐标系3个轴向上的主转动惯量;ω1、ω2和ω3分别为沿x轴、y轴和z轴的角速度分量.坐标系dqp由坐标系xyz分别绕x、y、z轴旋转α、β和γ得到,其坐标变换关系如图2所示.由文献[15]可得角速度转换矩阵为
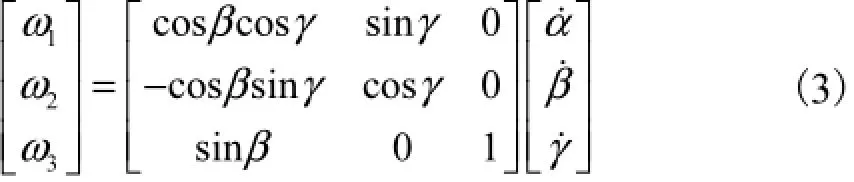
将式(3)代入式(2),得
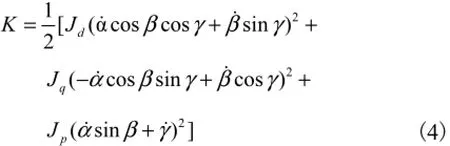

图2 笛卡尔坐标系变换关系示意Fig.2 Schemactic diagram of transformation between two Cartesian coordinates
由永磁球形电动机结构可以得出,其转子沿输出轴方向呈轴对称,于是Jd=Jq≠Jp,设Jd=Jq=Jdq,将式(4)代入式(1),由上述分析可知,这里Ε=Κ.则可得各轴向动力学方程
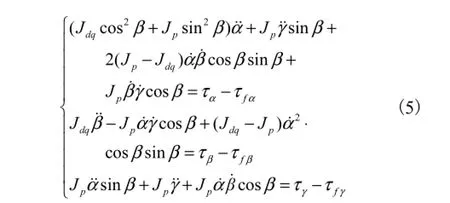
将式(5)写成矩阵形式为

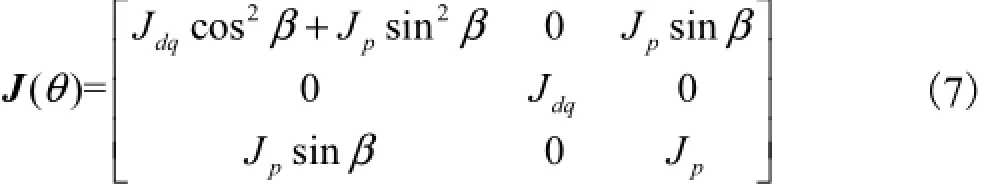
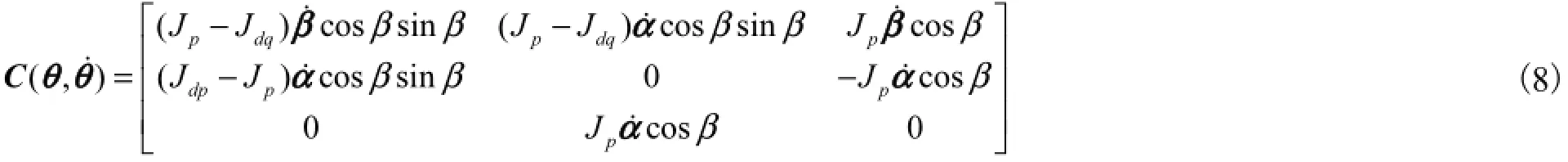
与文献[16]中所建立永磁球形电动机动力学简化模型相比,本文所建立完整模型提高了系统阶次,增加了系统的复杂度,更加接近实际系统,提高了控制系统的准确度.
3 基于计算力矩法的轨迹跟踪控制
3.1 基于计算力矩法控制器的设计
计算力矩法是一种基于模型的动力学控制算法,在机器人的控制领域得到广泛应用.从动力学系统角度出发,永磁球形电动机属于广义机器人的范畴,因此,利用计算力矩法对其进行动力学控制.计算力矩法控制律为

式中:τ 为控制转矩;u为伺服控制器,表达式为


忽略摩擦转矩τf,得

并且由式(7)可知J(θ)为非奇异矩阵,则

依据计算力矩法的原理,以永磁球形电动机的动力学模型为被控对象,设计相应的控制方案,其控制框图如图3所示.

图3 基于计算力矩法的控制方案示意Fig.3 Control block diagram of the computed torque method based algorithm
3.2 不确定因素分析
永磁球形电动机的实际控制中,需要对其动力学模型进行参数估计,并由此得出估计模型.估计模型与实际模型之间存在的模型误差构成了系统的结构化不确定性,外部扰动与摩擦转矩构成了系统的非结构化不确定性.在永磁球形电动机动力学控制方案中,对其模型的主转动惯量进行估计,构建估计矩阵,则估计的惯性矩阵与估计的哥氏力矩阵分别为

其中

其中
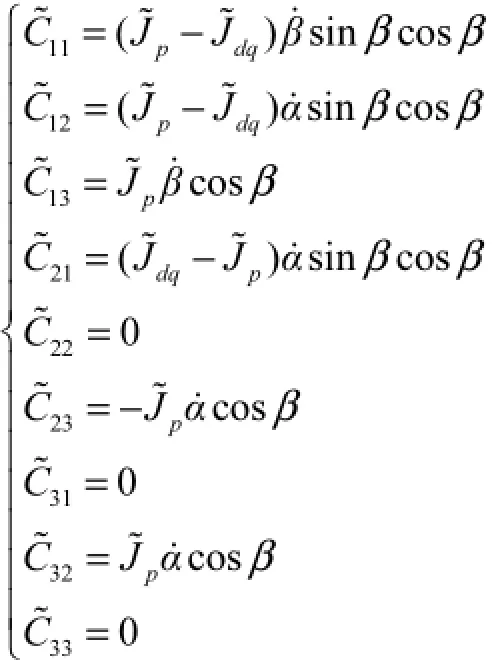

式(16)和式(17)定义的误差称为永磁球形电动机系统结构化不确定性;摩擦转矩、负载转矩和外部扰动等不易被精确建模的因素,称为永磁球形电动机系统的非结构化不确定性.
4 仿真结果与分析
根据图3所示的控制框图和计算力矩法的原理,在Matlab-Simulink搭建永磁球形电动机轨迹跟踪控制系统仿真模型,并对系统仿真结果进行分析.
为了比较永磁球形电动机简化模型和较完整模型的准确性,分别对2种模型下的α 轴向轨迹跟踪误差进行对比研究,采用以下2种仿真条件:①α、β和γ3个轴向的给定信号均为阶跃信号(初始时间为0,终值为1);②α、β和γ轴向的给定信号均为正弦信号y=sin(2πx/3).仿真结果如图4所示.
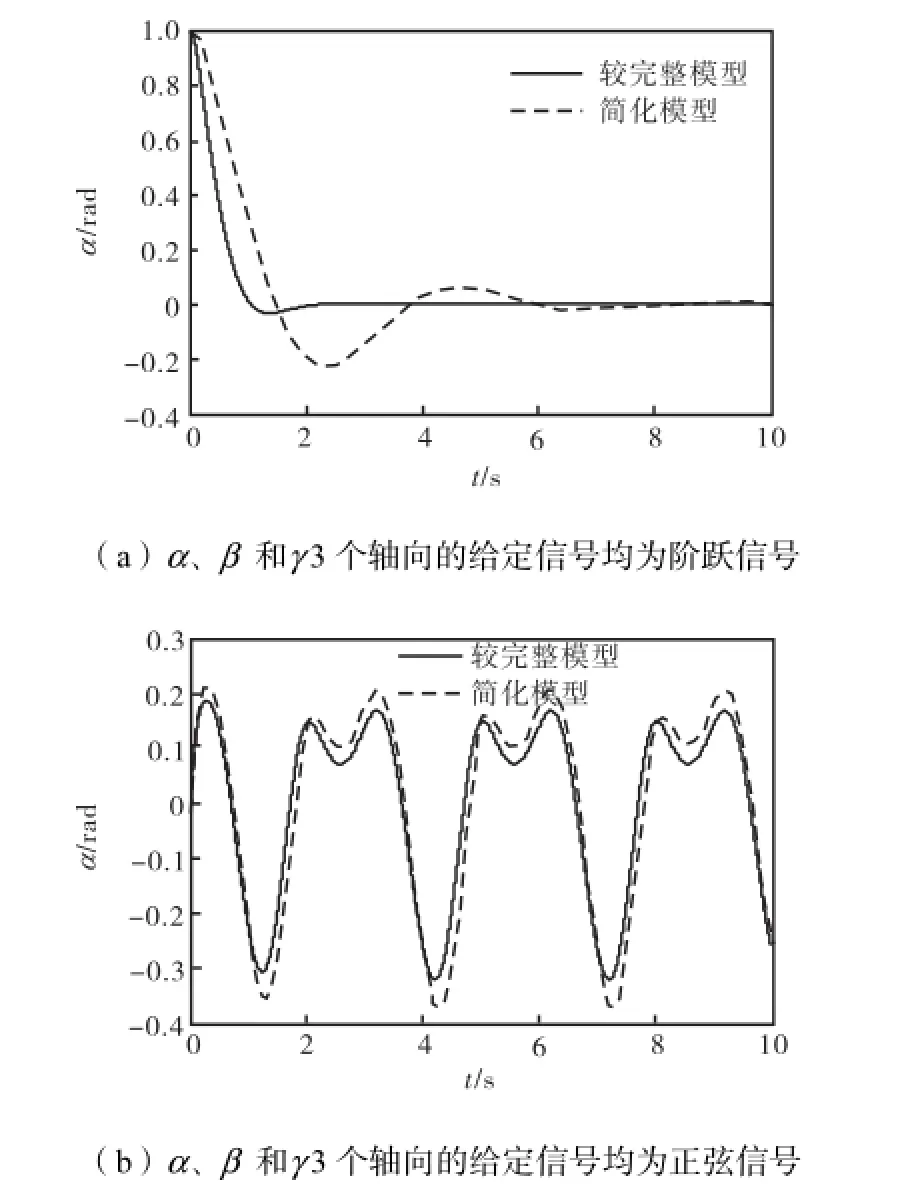
图4 α 轴向轨迹跟踪误差对比Fig.4 Comparison of trajectory tracking error of α-axis
由图4可以看出,永磁球形电动机较完整模型轨迹跟踪误差明显小于简化模型,从而证明本文所建立的完整模型更加接近实际系统.
基于永磁球形电动机较完整模型采用计算力矩法分析其3个轴向轨迹跟踪情况.图5为当3个轴向给定信号都为连续正弦信号y=sin(2πx/3)时,α、β和γ 3个轴向的轨迹跟踪情况示意.
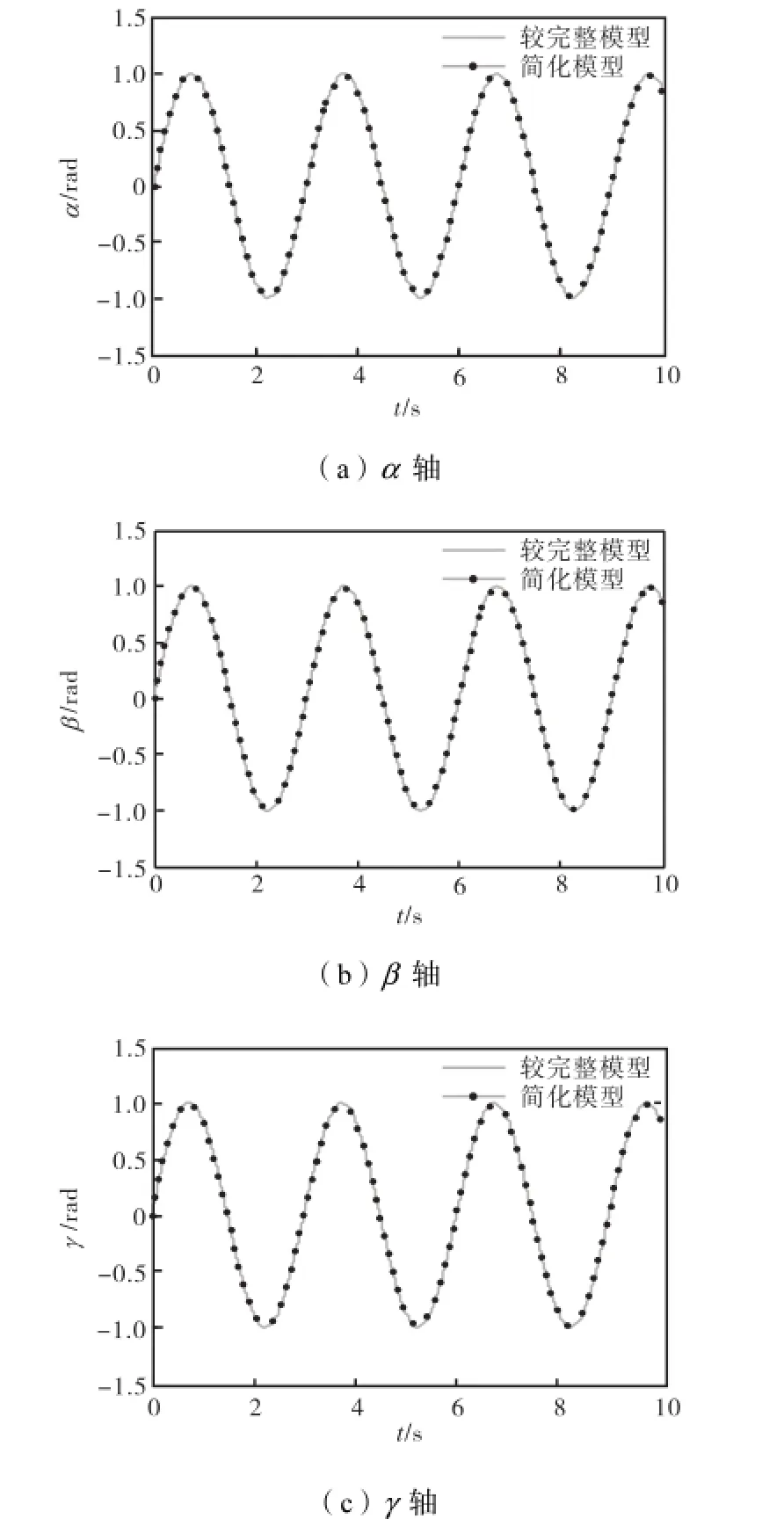
图5 3轴向连续轨迹跟踪结果Fig.5 Continous trajectory tracking results of three axes
由图5可以看出,采用计算力矩法时,跟踪轨迹可以较好地追踪给定轨迹,且稳态情况下跟踪误差基本收敛为零,实现了较高精度的轨迹跟踪,从而证明了此方法的有效性.
为了比较不同算法下的连续轨迹跟踪误差情况,分别采用PD算法、直接前馈补偿法和计算力矩法来进行仿真比较,图6为α、β 和γ 3个轴向的正弦信号跟踪误差对比情况.从图6中可以看出,计算力矩法对连续轨迹的跟踪误差明显小于其他2种方法,保证了控制的精度和响应速度.
为了进一步检验计算力矩法的解耦控制效果,给出以下3种情况:①α、β 和γ 3个轴向的给定信号均为阶跃信号(初始时间为0,终值为1);②α 轴向给定信号为阶跃信号,β轴向给定信号为正弦信号y= sin(2πx/3),γ轴向给定信号为余弦信号y= cos(2πx/3);③α 轴向给定信号为阶跃信号(初始时间为0,终值为1),β轴向给定信号为正弦信号y= sin(2πx/3),γ轴向给定信号为指数信号y=1-exp(-0.1,t2). 分别采用PD算法和计算力矩法,对α轴向的轨迹跟踪效果进行了仿真比较,如图7所示.

图6 3轴向连续轨迹跟踪误差对比Fig.6 Comparison of continous trajectory tracking error of three axes
从图7中可以看出,当采用PD算法时,3种情况下,α 轴向跟踪轨迹与给定轨迹之间存在较大的跟踪误差,其跟踪误差明显大于采用计算力矩法时的情况.由此可知,采用PD算法时β和γ轴向给定信号对α 轴向跟踪轨迹有较大的影响,说明各轴向间的交叉耦合影响严重,作为一种不基于模型的控制算法,PD算法较难实现永磁球形电动机的动力学解耦控制.当采用计算力矩法时,3种情况下,α轴向的输出信号均能较好地跟踪给定信号,轨迹跟踪误差较小,说明采用计算力矩法,可以有效削弱轴向间的交叉耦合影响,从而实现较为理想的解耦控制效果.
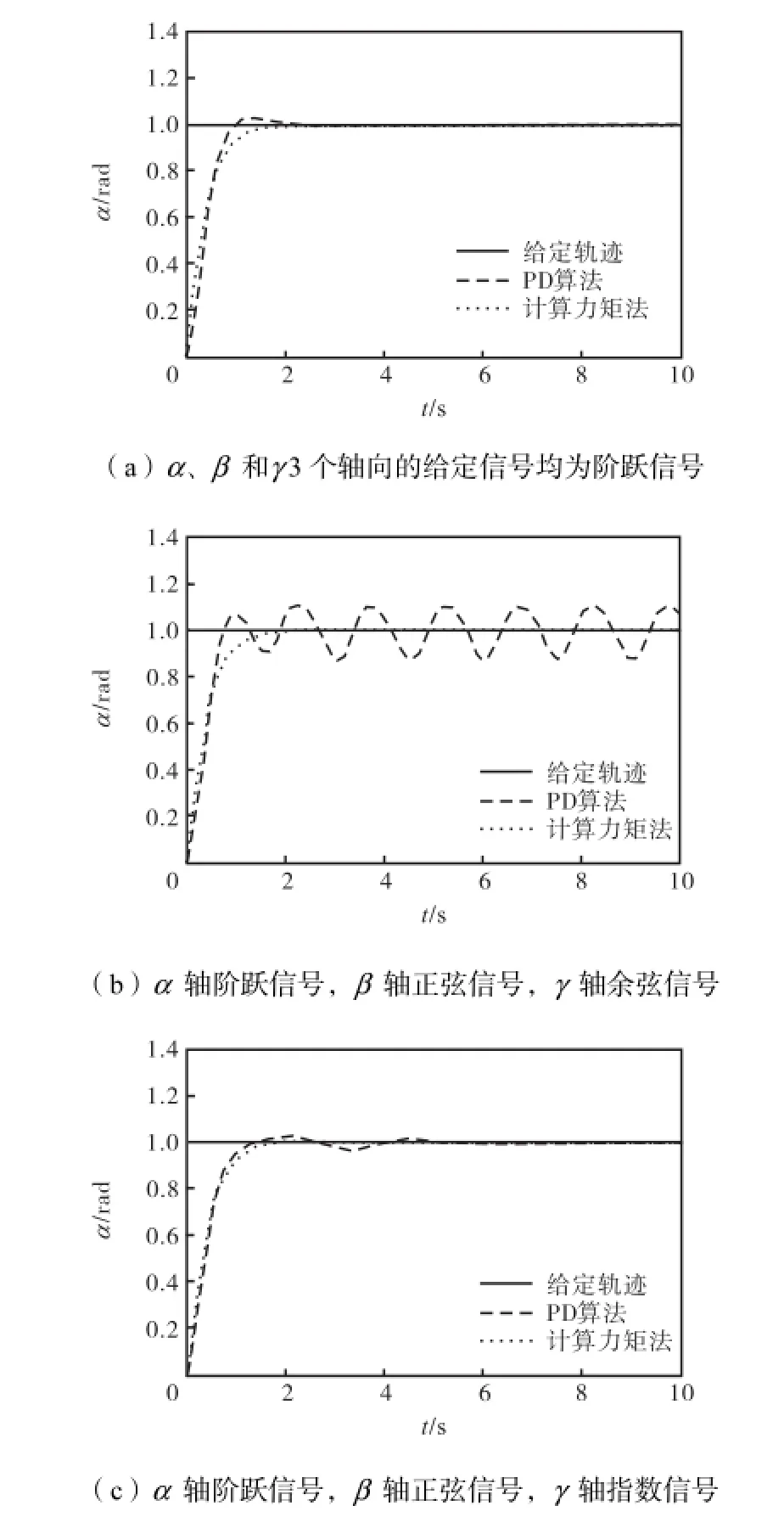
图7 不同算法的解耦效果对比Fig.7 Comparison of decoupling results of different methods
最后,对永磁球形电动机控制系统的鲁棒性进行检验.α、β 和γ 3个轴向的给定信号均为正弦信号y=sin(πx/3),即转速为n=10,r/min,分别从以下3种情况进行分析:①α、β 和γ 3个轴向分别在1,s时加入幅值为0.1,N·m和幅值为0.2,N·m的阶跃信号,即加入幅值为给定信号的10%及20%的突加负载,如图8(a)所示;②α、β 和γ 3个轴向分别加入幅值为给定信号的10%与20%均匀分布的随机扰动信号,如图8(b)所示;③系统模型参数分别为Jp1=1.1,Jp,Jdq1= 1.1,Jdq,如图8(c)所示.以上均以α 轴向轨迹的跟踪误差作为检验目标.
从图8(a)可以看出,当系统突加负载1与负载2时,α 轴向轨迹的跟踪误差与不加负载时基本吻合;由图8(b)可知,当系统存在有界的随机扰动时,α 轴向轨迹的跟踪误差很小,且2种随机扰动下跟踪误差基本不变;由图8(c)可知,无论简化模型,还是较完整模型,在系统模型参数变化时,α 轴向轨迹的跟踪误差仍然较小,并且跟踪误差基本不变.说明当系统在突加负载、存在有界的随机扰动以及系统模型参数变化的情况下,轴向轨迹跟踪误差基本不变,计算力矩法可有效抑制系统的不确定性因素对轨迹跟踪效果的影响,从而表明该算法具有较强的鲁棒性.
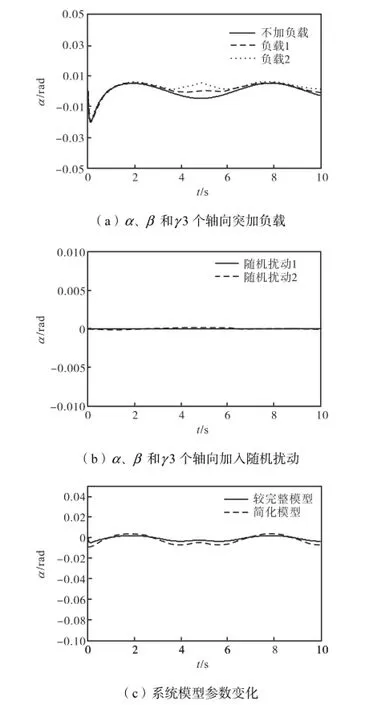
图8 α 轴向连续轨道跟踪误差比较Fig.8Comparison of continous trajectory tracking error of α-axis
5 结 语
永磁球形电动机动力学系统是一个多变量、非线性、强耦合系统.相比于简化模型,较完整模型更加接近于实际系统,提高了系统的准确性.轴向间存在强耦合性,严重影响了各轴向的轨迹跟踪性能.仿真结果表明,本文所提出并采用的计算力矩法可以有效地削弱轴向间交叉耦合的影响,显著改善运动性能,并对不确定因素的干扰具有一定的鲁棒性,相比普通的PD算法和直接前馈补偿算法,在轨迹跟踪控制方面具有较强的优越性,为永磁球形电动机运动控制的研究提供了新思路.
[1] Son Hungsun,Lee Kok-Meng. Distributed multipole models for design and control of PM actuators and sensors[J]. IEEE/ASME Transactions on Magnetics,2008,13(2):228-238.
[2] Kent D,George V,Richard P. The analysis of fields and torques in spherical induction motors[J]. IEEE Transactions on Magnetics,1987,23(1):273-282.
[3] 黄声华,陶醒世,林金铭. 三维电动机的电磁模型[J]. 电工技术学报,1994(4):17-20. Huang Shenghua,Tao Xingshi,Lin Jinming. Electromagnetic model of three-dimensional motor[J]. Transactions of China Electrotechnical Society,1994(4):17-20,40(in Chinese).
[4] Chirikjian G S,Stein D. Kinematic design and commutation of a spherical stepper motor[J]. IEEE/ASME Transactions on Mechatronics,1999,4(4):342-353.
[5] Wang Jiabin,Wang Weiya,Jewll G W,et al. A novel spherical permanent actuator with three degrees-offreedom[J]. IEEE Transactions on Magnetics,1998,34(4):2078-2080.
[6] Kahlen K,Voss I,Priebe C,et al. Torque control of a spherical machine with variable pole pitch[J]. IEEE Transactions on Power Electronics,2004,19(6):1628-1634.
[7] Stein D,Chirikjian G S. Mathematical models of binary spherical-motion encoders[J]. IEEE/ASME Transactions on Mechatronics,2003,8(2):234-244.
[8] Xia Changliang,Li Hongfeng,Shi Tingna. 3-D magnetic field and torque analysis of a novel halbach army permanent-magnet spherical motor[J]. IEEE Transactions on Magnetics,2008,44(8):2016-2020.
[9] Xia Changliang,Song Peng,Li Hongfeng. Research on torque calculation method of permanent-magnet spherical motor based on the finite-element method[J]. IEEE Transactions on Magnetics,2009,45(4):2015-2022.
[10] Xia Changliang,Guo Chen,Shi Tingna. A neural network identifier and fuzzy controller based algorithm for dynamic decoupling control of permanent magnet spherical motor[J]. IEEE Transactions on Industrial Electronics,2010,57(8):2868-2878.
[11] Son Hungsun,Lee Kok-Meng. Open-Loop controller design and dynamic characteristics of a spherical wheel motor[J]. IEEE Transactions on Industrial Electronics,2010,57(10):3475-3482.
[12] Stein D,Chirikjian G S,Scheinerman E R. Theory,design,and implementation of a spherical encoder [C]// Proceedings of the 2001 IEEE International Conference on Robotics and Automation. Seoul,Korea,2000:1773-1779.
[13] 王群京,陈丽霞,吴立建,等. 基于加权无向图的永磁球形步进电机运动控制[J]. 中国电机工程学报,2005,25(9):130-134.
Wang Qunjing,Chen Lixia,Wu Lijian,et al. The control of a permanent magnent spherical stepper motor based on weighted gpaph[J]. Proceedings of the CSEE,2005,25(9):130-134(in Chinese).
[14] 黄声华,陶醒世,林金铭. 三维电动机力学模型及解耦控制[J]. 电工技术学报,1996,11(1):12-16.
Huang Shenghua,Tao Xingshi,Lin Jinming. Mechanical model of three dimensional motor and its decoupling control[J]. Transactions of China Electrotechnical Society,1996,11(1):12-16(in Chinese).
[15] Guo Chen,Xia Changliang. A dynamic decoupling control algorithm for halbach array permanent magnet spherical motor based on computed torque method[C]// Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics. Sanya,China,2007:2090-2094.
Control for Trajectory Tracking of Permanent Magnet Spherical Motor Based on Computed Torque Method
Li Hongfeng1,Song Zhenhui1,Guo Chen2,Li Bin1
(1. School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China;2. Huaneng Renewables Corporation Limited,Beijing 100036,China)
The permanent magnet spherical motor(PMSM)is a multivariable,nonlinear and strong coupling system. The external disturbance,the evaluated error of parameters and model error all have a great influence on the control performance of the motor. In order to obtain a better static and dynamic performance,and improve the trajectory tracking performance,a trajectory tracking control strategy of PMSM based on a computed torque method was proposed. The simulation results indicate that the proposed method can effectively eliminate the influences of inter-axis nonlinear coupling,and has better robustness against the external disturbance and the model error. Furthermore on excellent tracking trajectory performance can also be realized.
permanent magnet spherical motor;dynamic model;trajectory tracking;computed torque method
TM320.13
A
0493-2137(2013)11-0991-07
DOI 10.11784/tdxb20131107
2012-06-07;
2012-10-19.
国家自然科学基金资助项目(51007061);天津市应用基础与前沿技术研究计划资助项目(10JCYBJC07900).
李洪凤(1979— ),女,博士研究生,副教授.
李洪凤,lihongfeng@tju.edu.cn.

