基于未确知测度的崩塌危险性综合评价模型研究及应用

何虎军 ，苏生瑞, ，王孝健，李鹏

(1. 长安大学 地球科学与资源学院，陕西 西安，710054；2. 长安大学 西部矿产资源与地质工程教育部重点实验室，陕西 西安，710054；3. 长安大学 地质工程与测绘学院，陕西 西安，710054)

我国是滑坡、崩塌和泥石流等地质灾害频繁发生的国家，而崩塌灾害是3大地质灾害常见灾害之一。由于崩塌突发性强，破坏性强，经常破坏公路、铁路和建筑物，给人类的生命和财产造成重大损失。尤其我国西部地区多为山区，地形地质条件极为复杂，山区公路一般沿沟谷、斜坡路段布线，公路两侧存在大量高陡斜坡，地震后高陡边坡多为抗震不利段，容易产生崩塌落石灾害，对于公路等交通基础设施造成严重破坏，给抗震救灾工作和灾区人民生产生活产生极大的影响。因此，开展崩塌地质灾害灾情评估研究的信息化、定量化和科学化将为区域地质灾害灾情评估提供强有力的支持，为区域地质环境可持续发展奠定基础[1-9]。目前，国内外在崩塌地质灾害危险性评价方面使用方法分为定性评价和定量评价2类[10]。其中定性方法又可分为野外地貌分析法和参数地图法。定量方法又可分为统计分析法和地理工程技术方法，近年来神经网络分析法也开始应用到地质灾害危险性定量评价中。虽然目前发展出很多方法，然而，这些方法大多存在一些不足：一方面，影响崩塌活动的因素众多，既有崩塌体本身所具有的内部特征，称为内因，如标高、坡度、地层岩性、土壤类型和土地利用情况等，又有诱发崩塌灾害发生的外部因素，称为外因，如地下水、降水、震动和各种人类活动等。大部分文献中只考虑其中某一指标的影响因素，评价指标不够全面；另一方面，现有研究文献中的半定量和定量模型本身存在一些不足，如模糊评判法不符合“非负有界性、可加性、归一性”的测量准则等特征，其“取大取小”原则也存在一定的不足，尤其在确定权值时有时采用专家打分法有一定的主观性[11]。本文作者在前人对崩塌地质灾害危险性研究及综合考虑影响崩塌地质灾害危险性的基础上，借鉴未确知测度评价模型的理论和思想，构建崩塌危险性未确知测度综合评价模型，用信息熵理论确定影响崩塌危险性各因素的权重，利用置信度识别准则对崩塌危险性进行评价，为崩塌危险性评价提供一种新的思路。

1 未确知测度模型的概述

设x1，x2，…，xn为n个对象，即指标空间X={x1，x2，…，xn}，每个评价对象有m个单向评价指标空间，即 I={I1，I2，…，Im}，则 xi可表示为一个 m维向量xi={xi1，xi2，…，xim}。对xi有p个评价等级，评价等级空间U={C1，C2，…，Cp}，其中Ck表示第 k个评价等级，设k级比k+1级强，即Ck＞Ck+1，则称{C1，C2，…，Cp}为评价空间U上的一个有序分割类。

1.1 单指标未确知测度

设μijk=μ(xij∈Ck)表示测量值 xij属于第k个评价等级Ck的程度，要求μ满足：

其中：式(2)称为μ对评价空间U满足“归一性”；式(3)称为 μ对评价空间 U“可加性”。满足式(1)，(2)和(3)的称为 μ未确知测度(uncertainty measure)，简称测度[12-18]。

称矩阵pmijk×)(μ为单指标测度评价矩阵，且有

在构建单指标测度评价矩阵时，首先要构建单指标测度函数，目前，单指标测度函数的构建方法主要有直线型、指数型、抛物线型和正弦型等。不管采用什么形式的模拟函数，“非负、归一、可加”的限制条件是必须被满足的。应根据具体指标的变化特点选用适当的未确知测度函数，直线型未确知测度函数是目前应用最广、最简单的测度函数，故本研究也采用直线型未确知测度函数。

1.2 指标权重的确定

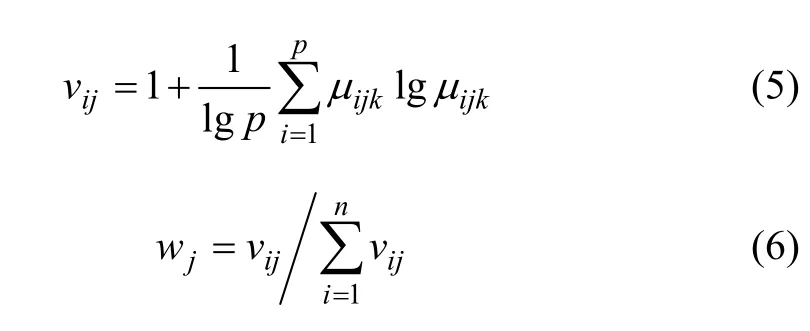
1.3 多指标综合测度

1.4 置信度识别准则

若C1＞C2＞…＞Cp，引入置信度识别准则，设λ为 置 信 度(λ≥0.5， 通 常 取 λ=0.6 或 0.7)则认为 xi属于Ck0。

1.5 排序

除了要判别xi属于那个评价等级外，有时要求对xi的重要程度排出顺序。若C1＞C2＞…＞Cp，令 Cl0的分值为 nl0，则 nl0＞nl+1，且有式中：qxi为评价因素 xi的未确知重要度，称q={qx1,qx2,…,qxp}为未确知重要度向量，可按 qxi的大小对xi的活动性重要区进行排序。

2 震后崩塌危险性评价指标体系

评价指标的选择是建立综合评价实体模型的基础，评价指标的数量和质量直接关系到评价的准确程度。由于影响崩塌危险性的因素多且复杂，结合有关研究崩塌危险性的指标体系，最终选取15项因素作为评价影响因子，即边坡坡形、边坡坡向、边坡坡度、边坡坡高、细观构造、出露结构面、地层岩性、软弱夹层、软弱面与临空面关系、多年平均降雨量、降雨冲刷作用、植被覆盖率、岩石风化程度、地震烈度、人类活动强度，分别用 x1，x2，x3，x4，x5，…，x15表示，其中对边坡坡形、边坡坡向、细观构造、地层岩性、软弱夹层、软弱面与临空面关系、人类活动强度用半定量化的方法进行取值，其分级标准及赋值情况见表 1。对边坡坡度、边坡坡高、出露结构面、多年平均降雨量、降雨冲刷作用、植被覆盖率、岩石风化强度、地震烈度用实测值进行评价，其分级标准见表1。对各评价指标进行分级及取值，评判集为{C1，C2，C3，C4}，即Ⅰ，Ⅱ，Ⅲ，Ⅳ级，分别表示危险性极高、危险性高、危险性中等和危险性低。

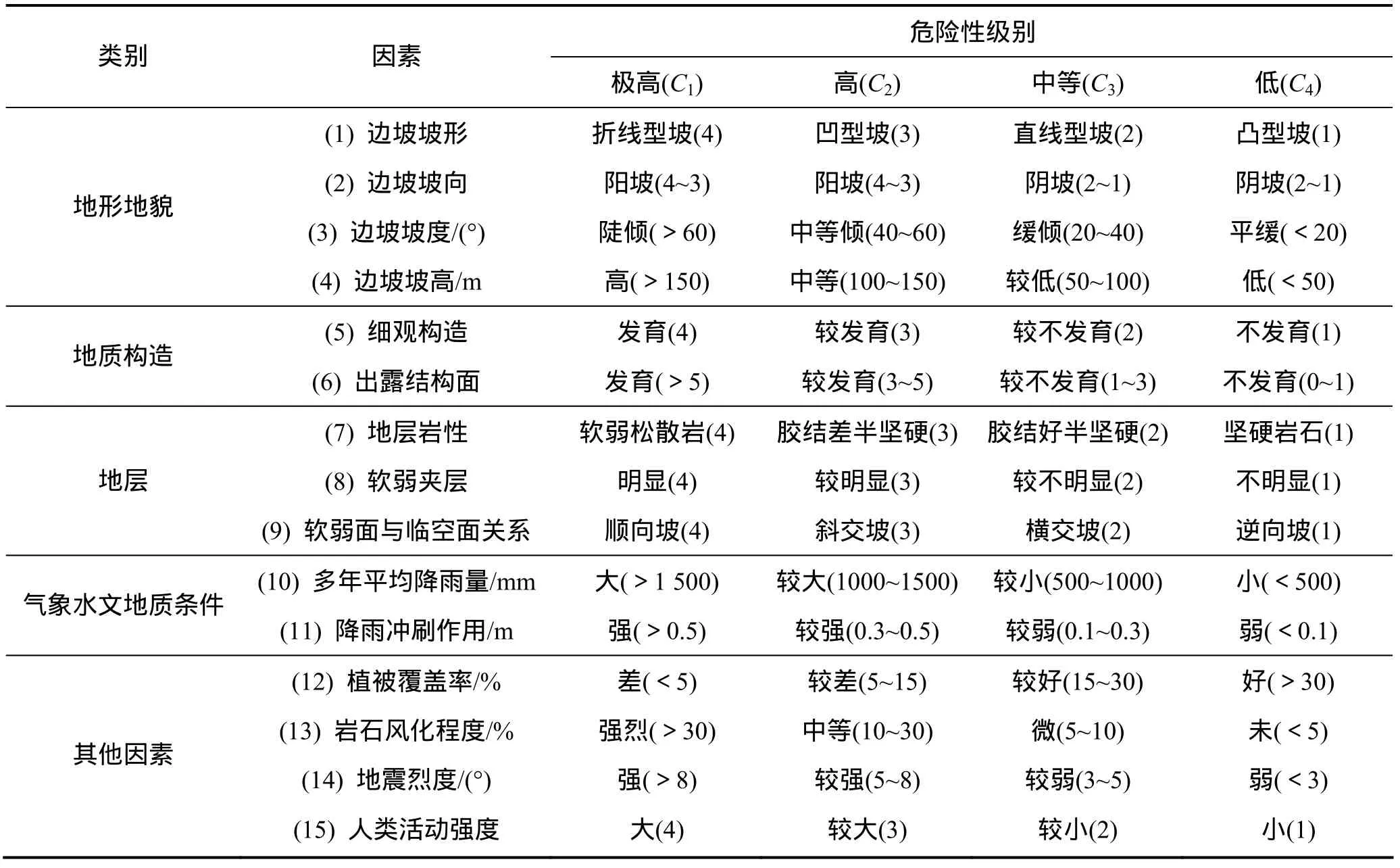
表1 评价因子及分级标准Table 1 Evaluation factors and grading standard

3 映秀－卧龙震后崩塌典型实例

研究区(S303映秀至卧龙段)处于四川省汉川县境内，四川盆地西北边缘，全长45.5 km，为一条横贯东西的重要干线公路，连接映秀和卧龙。坟川“5.12”地震之前，映秀至卧龙段已完成路面铺筑。该公路基本沿横穿龙门山构造带方向布线，起自中央主断裂(北川-映秀断裂)，穿龙门山后山断裂(茂县—汉川断裂)，地质条件复杂，是汉川地震灾区距震中最近的一条公路，也是地震地质灾害最为发育，损毁最为严重的一条公路。尤其是映秀至耿达段，75%道路被地震崩滑和泥石流堆积物掩埋。根据野外现场调查和相关资料分析，调查区内震后发育的崩塌灾害共99处。结合研究区水、工、环地质条件及崩塌自身的结构参数，本研究选择了其中17个崩塌点，分别对各影响因子进行取值。作为崩塌危险性的评价对象，各崩塌点基本情况见表2。

3.1 构造单指标测度函数

根据单指标测度函数的定义和表1的分级标准及表2具体取值，构建单指标测度函数，以便求得各评价指标的测度值。单指标测度函数分别见图1～9。

由表2中的取值，根据以上单指标测度函数，可以计算出 17个崩塌点的单指标测度评价矩阵。以BT05为例进行评判，可求得单指标测度评价矩阵为：

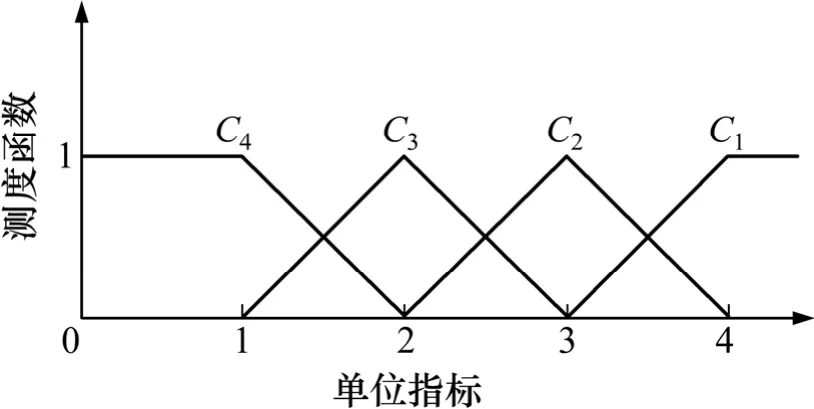
图1 边坡坡形、边坡坡向、细观构造、地层岩性、软弱夹层、软弱面与临空面关系、人类活动强度的单指标测度函数Fig. 1 Single index measure function of slope shape, aspect of slope, meso structure, stratum lithology, weakness interlayer,relationship among weakness face and free face and human activity intensity

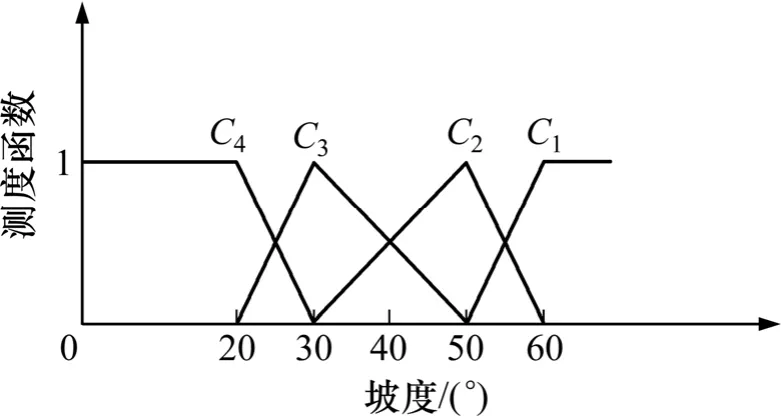
图2 边坡坡度单指标测度函数Fig. 2 Single index measure function of slope

表2 崩塌危险性评价指标调查统计表Table 2 Survey statistics table of landslide hazard evaluation index

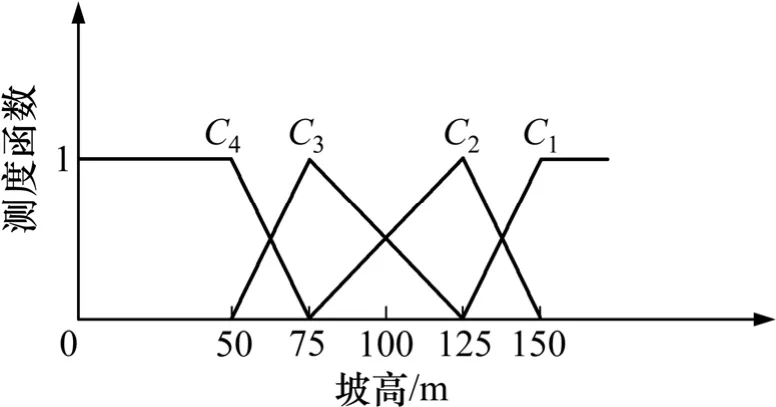
图3 边坡坡高单指标测度函数Fig. 3 Single index measure function of slope height of slope

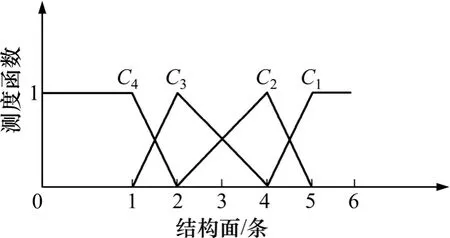
图4 出露结构面单指标测度函数Fig. 4 Single index measure function of exposed structural face

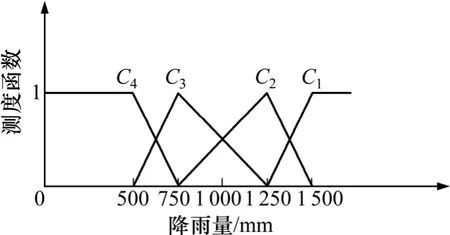
图5 多年平均降雨量单指标测度函数Fig. 5 Single index measure function of mean annual rainfall

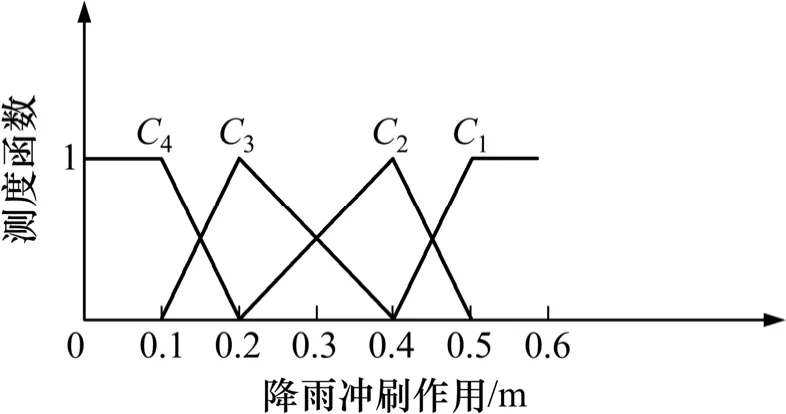
图6 降雨冲刷作用单指标测度函数Fig. 6 Single index measure function of rainfall erosion

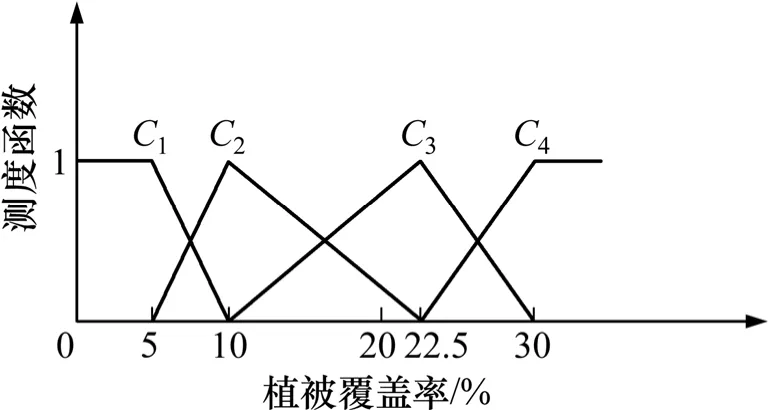
图7 植被覆盖率单指标测度函数Fig. 7 Single index measure function of vegetation cover rate

图8 岩石风化程度单指标测度函数Fig. 8 Single index measure function of weathering degree of rock

图9 地震烈度单指标测度函数Fig. 9 Single index measure function of earthquake intensity

3.2 计算多指标测度评价矩阵

用式(5)和(6)确定各评价指标权重，BT05评价指标权重{w1，w2，w3，w4，w5，…，w15}= {0.074 0.074 0.074 0.059 0.074 0.036 0.074 0.074 0.074 0.071 0.074 0.047 0.047 0.074 0.074}，根据单指标测度矩阵及多指标测度计算公式得出多指标测度向量为：μ1=ϖ1·μA1={0.260 0.246 0.258 0.236}。

3.3 置信度识别

取置信度λ=0.5，k0=0.506＞0.5，即该边坡危险性分级为II级高。同理，对其他16个崩塌点进行了评价。评价结果如表3所示。

表3 未确知测度模型评价结果Table 3 Evaluation results of uncertainty measure model

3.4 危险性排序

根据排序公式，因为 C1＞C2＞C3＞C4，取nl=10-2q，1≤q≤4，则有 q={5.060，4.720，5.046，4.786，3.822，4.012，5.120，4.540，4.940，4.720，4.880，4.690，5.180，4.980，5.040，5.080，5.000}。

对17个崩塌点的危险性按重要度进行排序，则崩塌危险性程度从大到小依次为YBT03，W28，BT05，BT13，W17，W33，W06，BT58，BT70，BT24，BT09，BT66，BT80，BT54，BT49，BT40，BT33。

4 结论

(1) 影响崩塌危险性的因素极其复杂多样，既有内部因素又有外部因素，针对目前对崩塌危险性评价和分析采用的理论方法存在的缺点和不足，运用未确知测度评价模型对崩塌危险性进行了评判。

(2) 根据崩塌危险性的影响因素和分级标准，运用未确知测度理论建立了崩塌危险性评价指标的未确知测度函数，利用信息熵权理论计算各指标的权重，按照置信度识别准则对崩塌危险性进行了评价，并对其活动性进行排序。

(3) 未确知测度评价模型更加科学客观合理，不仅能够克服单一指标评价及专家打分法对崩塌危险性评价结果的影响，还能确定崩塌危险性的等级及危险性重要程度的排序，为崩塌危险性评价提供了一种新思路。

[1] Hoek E, Bray J W. Roek slope engineering[M]. London: Inst of Mining and Metallurgy, 1981: 6-37.

[2] 唐红梅. 群发性崩塌灾害形成机制与减灾技术[D]. 重庆: 重庆大学资源与环境科学学院, 2011: 1-8.TANG Hongmei. Developing mechanism and mitigation techniques of massive collapse[D]. Chongqing: Chongqing University. College of Resources and Environmental, 2011: 1-8.

[3] 曾廉. 崩塌与防治[M]. 成都: 西南交通大学出版社, 1990:1-20.ZENG Lian. Landslide and prevention[M]. Chengdu: Southwest Jiaotong University Press, 1990: 1-20.

[4] Fall M, Azzam R, Noubactep C. A multi-method approach to study the stability of natural slopes and landslide susceptibility mapping[J]. Engineering Geology, 2006, 82(4): 241-263.

[5] Kanungo D P, Arora M K, Sarkar S. A comparative study of conventional, ANN black box, fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas[J]. Engineering Geology, 2006, 85(3/4):347-366.

[6] 李贡辉. 基于模糊综合评价方法的崩塌落石影响参数关系探讨[J]. 中国水运, 2008, 8(8): 67-69.LI Gonghui. Discuss on impact parameters relationship of landslide rockfall based on fuzzy comprehensive evaluation method[J]. China Water Transport, 2008, 8(8): 67-69.

[7] 张劲松, 杨红. 四川青川县碾子崩塌风险性评价[J]. 中国地质灾害与防治学报, 2012, 23(1): 33-38.ZHANG Jinsong, YANG Hong. Risk assessment for Nianzi rockfall in Qingchuan county, Sichuan province[J]. The Chinese Journal of Geological Hazard and Control, 2012, 23(1): 33-38.

[8] 李松. 震后公路边坡崩塌灾害分类与形成机理研究[D]. 西安:长安大学地质工程与测绘学院, 2011: 1-10.LI Song. Study on classification and formation mechanism of highway slope landslide disaster after earthquake[D]. Xi’an:Changan University. School of Geology Engineering and Geomatics, 2011: 1-10.

[9] 郭亚军. 综合评价理论、方法及应用[M]. 北京: 科学出版社,2008: 25-36.GUO Yajun. Theory, method and application of synthetic evaluation[M]. Beijing: Science Press, 2008: 25-36.

[10] 岳跃. 基于 GIS的崩塌地质灾害危险性评价研究[D]. 上海:同济大学土木工程学院, 2008: 20-30.YUE Yue. Study on hazard evaluation landslide geological disaster based GIS[D]. Shanghai: Tongji University. School of Civil Engineering, 2008: 20-30.

[11] 曹庆奎, 杨艳丽, 于瑞龙. 基于未确知集的煤矿安全评价[J].煤炭学报, 2007, 32(2): 181-185.CAO Qingkui, YANG Yanli, YU Ruilong. The coal mines safety appraisal based on unascertained set[J]. Journal of China Coal Society, 2007, 32(2): 181-185.

[12] 刘开第, 吴和琴, 庞彦军, 等. 不确定性信息数学处理及应用[M]. 北京: 科学出版社, 1999: 10-30.LIU Kaidi, WU Heqin, PANG Yanjun, et al. Mathematics treatment and application of uncertainty information[M]. Beijing:Science Press, 1999: 10-30.

[13] 刘开第, 吴和琴, 王念鹏, 等. 未确知数学[M]. 武汉: 华中理工大学出版社, 1997: 1-20.LIU Kaidi, WU Heqin, WANG Nianpeng, et al. Uncertainty mathematics[M]. Wuhan: Huazhong University of Science and Technology Press, 1997: 1-20.

[14] 宫凤强, 李夕兵, 董陇军, 等. 基于未确知测度理论的采空区危险性评价研究[J]. 岩石力学与工程学报, 2008, 27(2):323-330.GONG Fengqiang, LI Xibing, DONG Longjun, et al.Underground goaf risk evaluation based on uncertainty measurement theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 323-330.

[15] 李树刚, 马超, 王国旗. 基于未确知测度理论的矿井通风安全评价[J]. 北京科技大学学报, 2006, 28(2): 101-103.LI Shugang, MA Chao, WANG Guoqi. Colliery ventilation safety evaluation on the basis of uncertainty measure[J]. Journal of University of Science and Technology Beijing, 2006, 28(2):101-103.

[16] 朱兴琳, 方守恩, 王俊骅. 基于未确知测度理论的高等级公路交通安全评价[J]. 同济大学学报: 自然科学版, 2010, 38(7):1012-1017.ZHU Xinglin, FANG Shouen, WANG Junhua. Traffic safety assessment of high-grade highway based on uncertainty measurement theory[J]. Journal of Tongji University: Natural Science, 2010, 38(7): 1012-1017.

[17] 王飞跃. 基于不确定性理论的尾矿坝稳定性分析及综合评价研究[D]. 长沙: 中南大学土木建筑学院, 2009: 67-78.WANG Feiyue. Research on stability analysis and comprehensive assessment of the Tailing dam based on the uncertainty theory[D]. Changsha: Central South University.School of Civil Engineering and Architecture, 2009: 67-78.

[18] DONG Longjun, PENG Gangjian, FU Yuhua, et al.Unascertained measurement classifying model of goaf collapse prediction[J]. Chinese Journal of Coal and Engineering, 2008,12(2): 221-224.