顾及约束的网络道路三维模型简化方法

蒲浩 ，李伟 ，赵海峰 ，宋占峰

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 高速铁路建造技术国家工程实验室，湖南 长沙，410075)

近年来，随着计算机网络技术的飞速发展，人们已经不满足Web页上二维空间的交互特性，而希望将万维网变成一个立体空间，以互联网为信息载体的网络三维可视化技术由于其表现形式直观生动，可跨越时间和空间的限制，有效地实现数据共享，已成为当前可视化技术新的发展方向，并被《国家中长期科学和技术发展规划纲要(2006—2020年)》[1]列为重点发展的前沿技术。道路工程的网络交互式三维可视化在可视化的协同设计，道路建设与运营的远程管理等领域有着广阔的应用前景，现已成为构建“数字公(铁)路”必不可少的基础核心技术。道路三维模型数据通常呈海量，将所有数据传输到客户端再进行可视化显然不可行。如何对网络环境下的道路三维模型进行简化，实现海量数据的高效压缩，并在客户端实时重构出令人满意的三维模型是实现道路三维可视化的关键。模型简化是采用适当的算法减少模型的面片数、边数和顶点数，在保证视觉效果的前提下，尽量降低模型的复杂度，从而满足模型数据实时传输与显示的要求。针对模型简化技术，国内外学者开展了一系列的研究，其中：Hoppe等[2-3]提出了经典的基于边折叠的渐进网格简化方法；Garland[4]针对渐进网格提出了简单有效的二次误差度量方法；近年来，付鑫等[5]提出了基于频度中心理论的三维模型的简化方法。刘湘云和邹北骥[6]提出了一种基于概率值简化三角形网格模型的新算法，加快了简化速度；冯翔和周明全[7]综合考虑了模型几何信息以及纹理信息的全局误差提出了一种带纹理的三角形网格模型简化算法。胡于进等[8]提出一种带属性的边折叠网格简化方法，较好地保留了原模型的物理属性特征。文献[9-14]对Garland[4]的二次误差度量方法进行了各种改进，使简化后模型的重要几何特征得到较好的保留。Atlan和Garland[15]针对大规模地形模型的特点提出相应的简化方法。上述方法在一定程度上实现了复杂三维模型的简化，为实现模型的网络交互式可视化奠定了基础，但仍存在以下问题：(1) 主要面向单机环境下的模型简化，不适于网络三维模型。(2) 主要针对无约束边界的三维模型，而道路模型中存在大量的约束边(路肩线、坡脚线等)，无法适用。因此，本文作者针对含有大量约束边界的道路三维模型的简化技术进行深入研究，提出顾及约束的网络道路三维模型简化方法，建立顾及约束的误差度量和视相关重构准则，实现大规模道路三维模型的高效压缩和实时动态传输。

1 总体实施方案

网络环境下道路三维实时交互式可视化的总体实施方案如图1所示，主要包括以下3个关键技术内容：

(1) 道路三维整体建模：基于约束Delaunay三角网理论，在服务器端建立道路三维整体模型。

(2) 服务器端三维模型简化：提出顾及约束的误差度量准则，在服务器端基于该准则，采用半边折叠操作对道路模型进行整体简化，同时构建半边折叠操作层次树，存入服务器端数据库。

(3) 客户端三维模型重构：建立视相关重构准则，在客户端，基于该准则，依据视点位置从服务器端的操作层次树上获取必要的模型细化信息，对模型进行细化，实现道路模型的视相关重构。

图1 总体实施方案图Fig.1 Overall implementing scheme

其中，关于道路三维整体建模方法，本文作者已有详述[16-17]。本文重点介绍后面2个关键技术。

2 服务器端顾及约束的道路模型简化

2.1 半边折叠与点分裂

道路三维整体模型为含有大量约束边界的三角网模型。针对三角网模型简化，Hoppe[2]的渐进网格提供了一种典型的简化模式。渐进网格是一个具有任意层次的多分辨率网格模型，这种特点非常适用于渐进传输和三维几何压缩等方面。如图2所示，原始网格模型 Mn通过一系列边折叠(fecol)操作来渐进地简化为基网格M0。

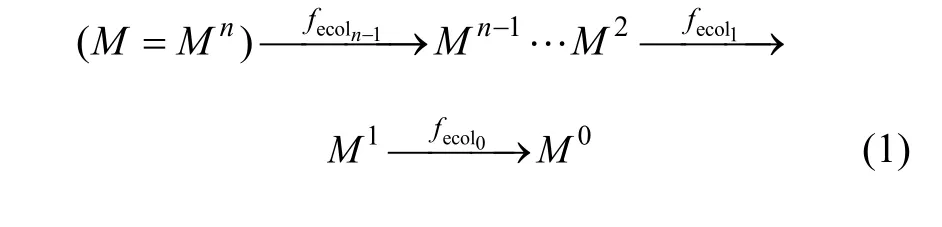
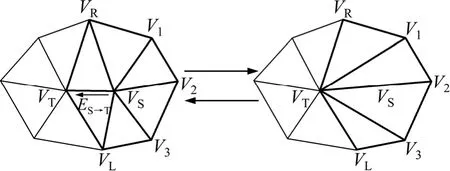
图2 半边折叠与点分裂操作Fig.2 Half-edge collapse and vertex split

相反，通过逆变换点分裂(fvsplit)操作可将基网格M0，渐进细化为Mn。

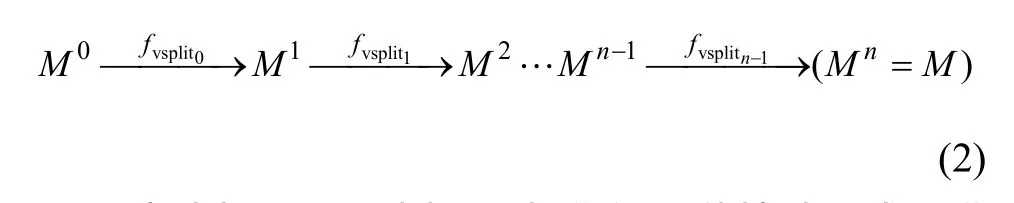
“半边折叠”是“边折叠”操作的一种特殊形式。进行“边折叠”时需要计算新的顶点位置，而“半边折叠”则以折叠边上的某个点作为新顶点的位置，而且操作记录中只需要记录1个顶点的坐标，可显著减少操作的时间和数据量。虽然在相同细节层次上半边折叠网格的质量不如边折叠网络的质量，但由于数据量显著较少，在相同时间内可获得更高层次细节的网格模型，因此，更适合模型的网络传输。

2.2 顾及约束的误差度量

在半边折叠过程中，选择合适的半边折叠误差度量方法是决定优质网格简化、重构效果和速度的关键。Garland[4]提出经典的二次误差度量(QEM)，Atlan[15]证明了该方法简单有效，但该方法未考虑模型中的约束边，不适于道路模型。虽然可以通过对此类半边折叠赋予极大误差值的方式来保证在简化过程中不改变约束边，但是，道路三维模型中约束边数量多，在简化过程中始终保留所有约束边，模型得不到有效地简化，基网格数据量大，而且容易出现大量的狭长三角形，模型质量不理想。因此，本文作者在 QEM基础上，提出顾及约束的误差度量(CQEM)。该方法不仅考虑对任意边进行简化时产生的几何误差，而且考虑对约束边的影响，对此类误差进行适当放大，保证在进行模型重构时可以优先恢复出约束边，具有较好的模型质量。

2.2.1 概念与定义

道路三维网格模型M可由顶点集V=(V1，V2，…，Vn)和三角形集合T=(T1，T2，…，Tm)所组成的二元组(V，T)来表示。为便于论述CQEM的基本原理，首先引入一些基本定义。

定义1 设VS，VT是三角网M中任意三角形Ti上的2个顶点，则记ES→T和ET→S分别为三角网中VS指向 VT和 VT指向 VS的2条有向边。ES→T，ET→S构成有向边对。对于有向边 ES→T，顶点 VS，VT分别为该有向边的起点和终点。

定义2 对于三角网中任意有向边ES→T，如果起点VS∈UCV，其中UCV为构成三角网约束边的顶点集合，则该有向边为约束有向边，否则，为无约束有向边。若ES→T，ET→S均为约束有向边，则ST为全约束边，若ES→T和ET→S均为无约束有向边，则ST为无约束边，否则，为半约束边。

定义3 三角网M中任意顶点VS，能与该顶点构成有向边的顶点称为其邻接点，所有邻接点构成的集合称为邻接点集，记为 VAdj,VS。VAdj,VS中所有顶点按逆时针方向排列形成的区域称为顶点VS的1阶邻域。

定义 4 具有相同顶点 VS的所有三角形构成的集合称为该顶点的邻接三角形集，记为 TAdj,VS。具有相同有向边的三角形构成的集合称为该有向边的邻接三角形集，记为 TAdj,ES→T。当该有向边处于三角网边界时， TAdj,ES→T包含1个三角形，否则，包含2个三角形。对于邻接三角形集有以下2条性质：

(1) 有向边对的邻接三角形集相同，即TAdj,E S→T= TAdj,ET→S；

(2) 有向边的邻接三角形集为该有向边起、终点邻 接 三 角 形 集 的 子 集 ， 即 TA dj,E S→T∈ TAdj,VS，TAdj,E S→T∈ TAdj,VT。

所有半边折叠操作均可用三角网中的一条有向边的相关信息来表示。如图2所示，该半边折叠操作删除有向边ES→T及邻接三角形集 TAdj,ES→T，并修改有向边起点VS的邻接三角形集 VAdj,VS，该半边折叠操作记为fE colS→T。

2.2.2 半边折叠误差计算

半边折叠 fEcolS→T对整个三角网模型的影响范围为起点VS的1阶邻域，误差度量仅需考虑VS的1阶邻域，本文提出的顾及约束的误差度量计算公式如下：

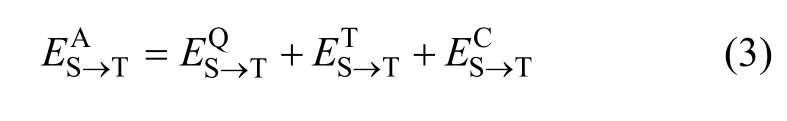
令：

则：

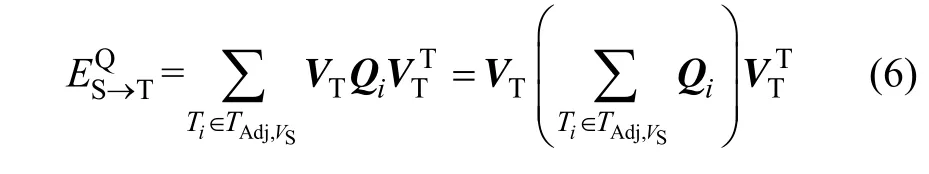
半边折叠中待删除的有向边邻接三角形如图3所示。有向边终点VT是 TAdj,ES→T上的点，VT到 TAdj,ES→T中三角形面片的距离为 0，中无法考虑删除TAdj,ES→T对三角网的影响，故CQEM计算公式中采用第2项计算该误差。删除 T 中三角形引起Adj,ES→T的误差与三角形的面积及三角形面片之间的夹角有关，面积越大，则夹角越大，对整个模型的影响就越大。对于三角网内部的有向边， TAdj,ES→T中包含2个三角形ΔSTL，ΔRTS。计算公式如下：

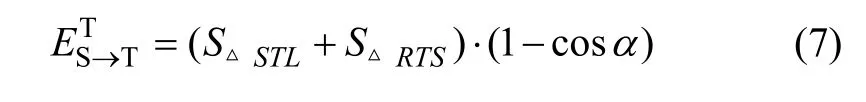
其中：SΔSTL，SΔRTS分别为2个三角形面积，可由边S，T，L，R的 4个顶点向量 VS，VT，VL，VR进行简单的矢量运算得出。α为2个三角形面片法向量夹角，cos α通过2个三角形的单位法向量点乘即可，计算公式如下：

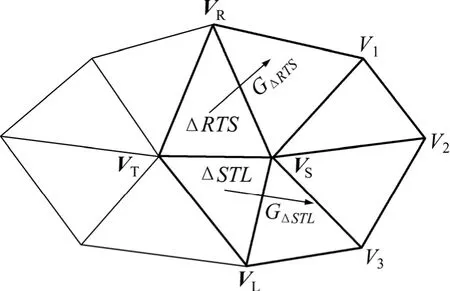
图3 半边折叠中待删除的有向边邻接三角形Fig.3 Adjacent triangle to be deleted in half-edge collapse

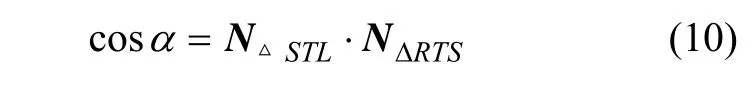
当有向边ES→T处于三角网M边界上时，TAdj,ES→T仅有1个三角形SΔSTL。此时

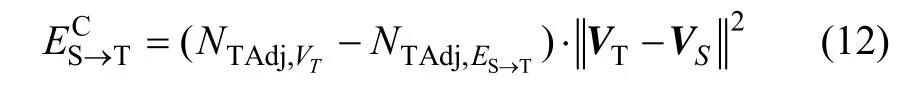
其中：N A dj,VT，N Adj,ES→T分别为顶点VT和有向边ES→T的邻接三角形个数。是对约束顶点进行半边折叠时误差的适当放大，可确保对半约束边进行折叠时总能保留约束顶点，现证明如下。

证明：设ST为三角网中任意一条半约束边，ES→T为约束有向边，ES→T为无约束有向边。

由于 VS在 TAdj,ET→S中的三角形上，距离为 0，则有：

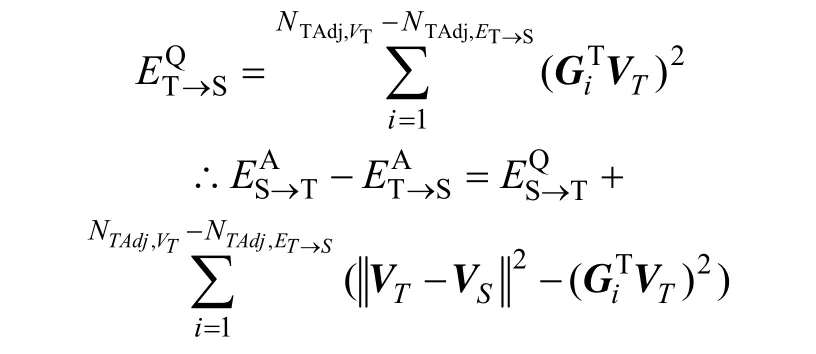
VT为三角形面片Ti上的点，||VT-VS||2为VS到VT的空间距离的平方和， (VT)为VS点到平面Ti的垂直距离平方和。由于点到平面上任一点的距离一定不小于该点到平面的垂直距离，故

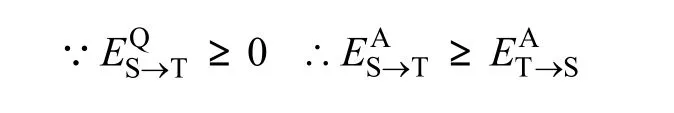
因此，对一端为约束点，一端非约束点的半约束边 ST进行折叠时，总能使得约束顶点得到保留，从而保留约束边。而对于两端均为约束顶点的全约束边，无论折叠过程中删除哪个顶点都需要增加该项，一般只有当边长相对很小时，全约束边的折叠误差才会小于周围的无约束边，先行折叠，而边长很小的约束边对可视化效果贡献不大，应当先进行简化，这是符合模型简化要求的。针对约束顶点增加的只是对半边折叠误差的适当放大，当周围存在着边长或者折角较大的三角形时，约束顶点也可被折叠，从而有效避免狭长三角形的出现，而且约束顶点参与简化，简化率也可得到显著提高。

2.3 建立操作层次树

半边折叠操作序列一般按半边折叠的顺序采用堆栈进行存储，越先折叠的边越早被分裂出来，但这不利实现客户端道路三维模型的视相关重构，如果待分裂的边位于堆栈的底部，则需要进行大量的点分裂操作才能实现视点范围内模型的细化。因此，应采用可尽量减少操作之间相关性的数据结构来存储操作序列，本研究采用如图4所示的操作层次树对半边折叠操作进行存储。操作层次树上每个结点记录1条有向边的半边折叠操作，子结点的半边操作依赖于其父结点，越早进行半边折叠，结点越处于操作树的顶端。在层次树中向上遍历结点则表示边折叠(简化)，向下则为点分裂(细化)。客户端进行实时交互浏览时，将依据视相关重构准则，选择出当前视点必要的操作结点即活动结点(如图5)，然后将需要更新的活动结点数据传输给客户端，最终在客户端绘制当前视相关网格。

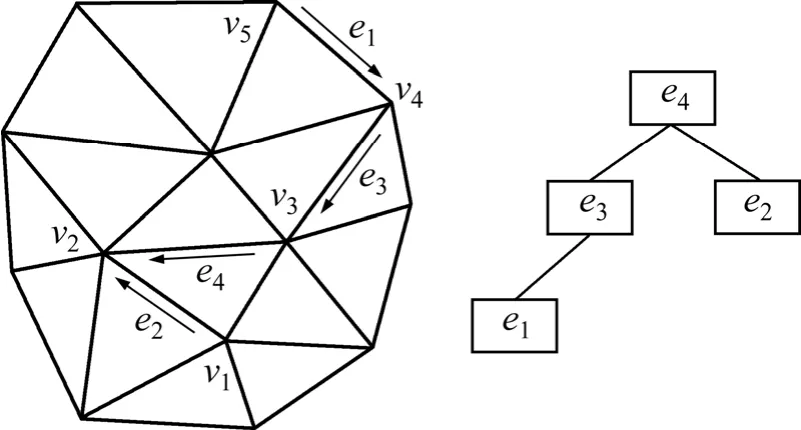
图4 半边折叠操作的层次结构Fig.4 Structure of half-edge collapse

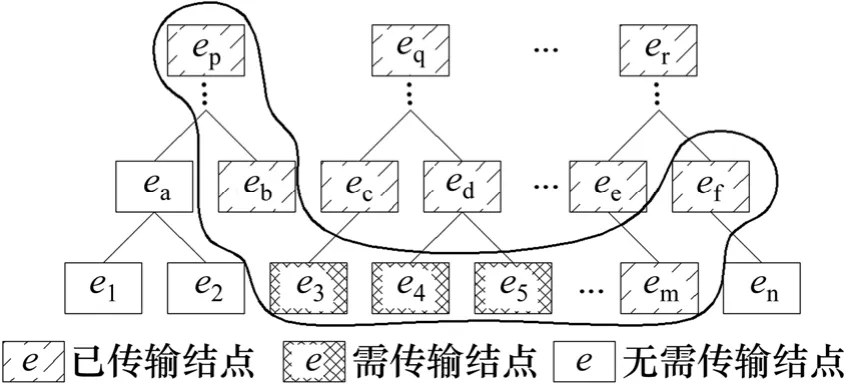
图5 基于层次结构的视相关重构Fig.5 View-dependent reconstruction based on level structure

为建立较为平衡的操作层次树，减少操作的依赖性，需要在三角网范围内均匀地选择折叠边[16]。为此，对有向边进行网格管理，按照客户端的浏览需求将整个场景划分为一系列大的网格区域，落在同一网格区域内的有向边按误差值用链表存储起来，误差越小，越在网格链表的前部，越早进行折叠。在进行模型简化时采用各网格首条有向边轮流折叠的策略，即先采用快速排序算法将网格数组按点数从小到大排序，依次对排好序的各网格取首条有向边进行折叠，并更新其有向边链表，轮流折叠，简化至基网格止。

3 客户端视相关模型重构

为减少远程客户端所需的数据量，缩短客户端等待时间，客户端在接收完基网格之后，应根据视点只获取必要的网格细化信息。对此，本文作者建立包括视锥准则、面向准则、轮廓准则及屏幕投影误差准则在内的视相关重构准则和约束边优先策略。只有同时满足这些重构准则的结点才需要将网格重构数据发送至客户端。同时，为保证距离视点较近的约束边可优先重构，采用约束边优先策略对待传输结点进行重排序。在视相关准则计算中，需要用到结点的包围球和法向锥。

定义5 结点包围球：对于结点t，其包围球是以t对应的有向约束边起点为中心，其半径r包围约束边起点的1阶邻域和t的所有子孙的球体。

定义6 结点法向锥：以结点t对应的有向边起点VS为圆锥顶点，VS的1阶邻域内三角形的单位平均法向量为轴线，VS平均法向量与这些三角形面最大的夹角θ为半角的圆锥称为法向锥，它包含了顶点VS的1阶邻域内三角形的法向量和t的子孙的法向量。

图6所示为视锥准则。如图6所示，e当前为视点，n为单位化的视线方向矢量，w为视野角的一半，dN，dF分别为近，远裁剪面到视点距离，v为结点 t包围球中心。如果a+b＜d且dN＜c＜dF，结点包围球在视锥内，可能需要进行细化。其中：

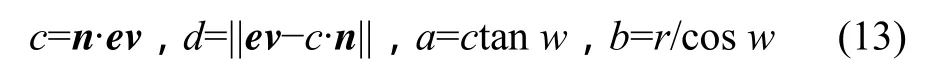
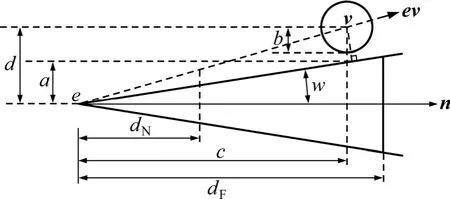
图6 视锥准则Fig.6 View cone criterion

图7所示为面向准则。对于结点t，若它关联的法向锥是面向视点的，则对结点t可能需要进行细化。如图7所示，结点t法向量nv，法向锥半角θ，nv与ev的夹角α，如果下式成立，则法向锥是面向观察者的：

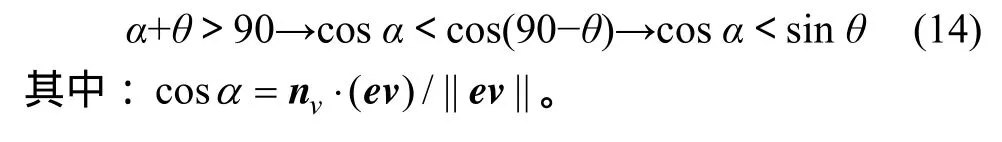
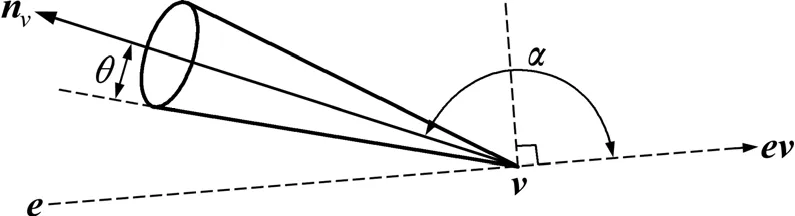
图7 面向准则Fig.7 Face criterion

图8所示为轮廓准则。在远程浏览中应尽可能获得轮廓边信息。如图8所示，如果下述一个不等式成立，该结点对应的有向边是轮廓的一部分，可能需要进行细化。

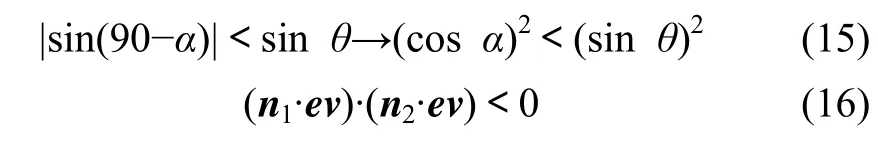
图9所示为屏幕投影误差准则。为减少网络传输量，只有在屏幕上绘制时其大小大于给定误差阀值 τ的三角形才需要绘制。如图9所示。如下式成立，则对应的结点t的有向边可能需要细化。

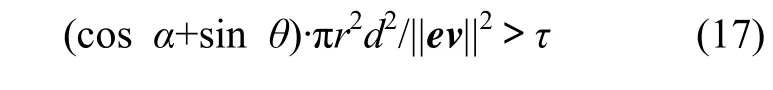
图8 轮廓准则Fig.8 Outline criterion

图9 屏幕投影误差准则Fig.9 Screen projection error criterion

约束边优先策略：如果在视点可见范围内这些约束边上的点尚未重构出来，尤其是在距离视点较近处，三维模型中将出现令人无法接受的变形。因此，在通过以上 4项准则选取操作层次树中对应需细化结点后，还需按如下方法对结点进行排序：

(1) 根据结点是否含约束有向边，将无父子关系的结点集L分为约束结点集Lc及无约束结点集Ln；

(2) 计算视点到所有结点包围球球心的距离di；

(3) 按 di由小到大对 Lc和 Ln分别进行排序得到Lc′和 Ln′；

(4) 将Lc′插入到Ln′前，形成约束边优先的活动结点列表L′。

通过以上方法形成的约束边优先活动列表L′可保证距离视点越近的约束边越早被分裂出来，而后是距离视点较远的约束边，最后按由近及远的方式分裂非约束边。该方法可有效地避免三维模型由于约束边未分裂出而产生的模型变形失真，保证三维模型的视觉质量。

值得注意的是，本文的模型简化和视相关重构是2个可逆的过程。当视点距离道路模型较近时，可完全无损地恢复出简化前的原始道路模型。客户端最终获得的模型精度仅与建立道路整体三维模型时的数据精度有关。

4 实验与应用

本研究对含25 849 366个三角形的高速公路三维模型进行实例测试。对原始模型进行简化后，形成的基网格仅有2 079个三角形。图10所示为该高速公路某区段的三维网格模型，道路的路肩线和坡脚线作为约束边(采用粗线表示)。从图10(b)中可以看出：模型基网格中道路模型的路肩线由于边长较短已经被简化，坡脚线由于与地形面片之间的夹角交大，少量得到保留，可以看出道路的大致轮廓。图10(c)所示为客户端动态浏览时的重构出的视相关网格模型，距离视点较近的网格已达到原始模型精度，距离较远的网格模型较为粗糙，但约束边界已清晰可见。

网络动态浏览测试时，服务器采用 IBM X3650 M3专业服务器(Xeon X5690 3.46G CPU， 32G内存)，客户端采用普通微机(Pentium 4双核 2.8 GHz CPU、2 G内存、GeForce FX 5200显卡)，在4 Mb/s带宽下，访问系统时，客户端的平均初始等待时间为3.8 s。在即可获得原始精度的三维模型，当视点发生跳转时，400 ms以内可观察到约束边，1 500 ms以内可观察到网络三维浏览过程中，当视点平滑移动时250 ms以内原始精度的三维模型，浏览过程中可达到20帧/s以上的帧速，具有流畅的速度和理想的三维可视化效果。

图10 高速公路某区段的三维网格模型Fig.10 3D mesh model of one highway segment

综合上述原理与方法，应用Wed3D技术，本文作者采用Visual Studio 2005和OpenGL开发“高速公路建设管理网络三维可视化信息系统”。该系统建立B/S架构下的高速公路及其建设管理信息的三维交互式浏览、查询、分析平台。已在常德至吉首、醴陵至茶陵、广元至巴中等高速公路的建设管理中成功应用。图11为广巴高速公路网络三维可视化效果。

本文提出的方法也可应用于各阶段的道路设计，为远程的道路三维设计提供技术支持。简化后的模型通过视相关重构可无损地恢复到原始模型，因此，只需按不同设计阶段的精度要求在服务器端建立原始三维模型，设计人员便可在客户端获得相应精度的三维信息，并在此基础上进行道路设计。

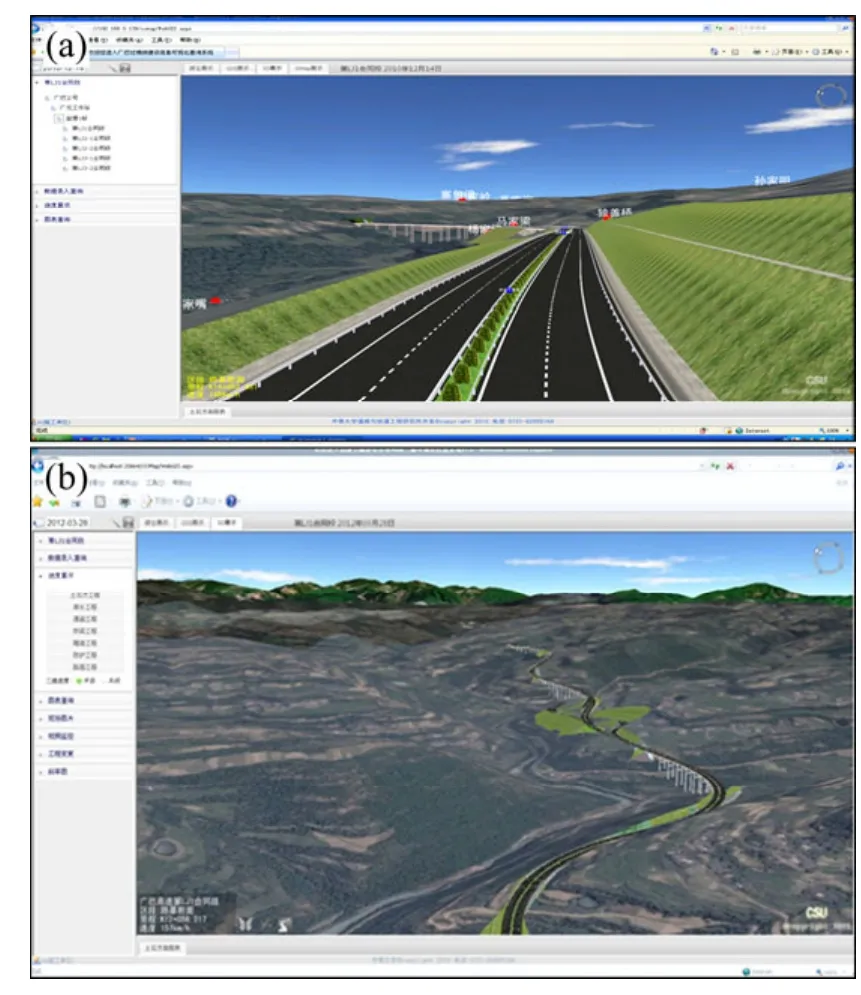
图11 广巴高速公路网络三维可视化Fig.11 Web-based 3D visualization for section of Guangyuan-Bazhong highway

5 结论

(1) 顾及约束的半边折叠误差度量方法，使约束边上顶点可参与简化，显著提高简化率，同时可视范围内约束边又可快速恢复，保证模型网格质量，解决了含大量约束边的道路模型简化问题。

(2) 远程视相关网格重构准则与约束边优先策略可在半边折叠操作层次树上快速确定需要传输到客户端的最小模型细化数据，使网络传输的数据量大大减少，解决了带宽与海量道路模型数据之间的矛盾。

(3) 基于上述方法开发的网络道路三维可视化系统已在高速建设管理中成功应用。应用结果表明可实现大规模公路三维场景的远程实时交互式可视化，具有令人满意的可视化效果。

(4) 该方法具有通用性，可扩展应用到其他含大量约束边的大规模三维模型。

[1] 中华人民共和国国务院.国家中长期科学和技术发展规划纲要(2006—2020)[EB/OL][2012-07-31]. http://www.gov.cn/jrzg/2006-02/09/ content_183787.htm.The State Council of the People’s Republic of China. National medium and long-term science and technology development plan(2006—2020)[EB/OL][2012-07-31]. http://www.gov.cn/jrzg/2006-02/09/ content_183787.htm.

[2] Hoppe H. View-dependent refinement of progressive meshes[J].Computer Graphics, 1997, 31(3): 189-198.

[3] Hoppe H, Derose T, Dechamp T, et al. Mesh optimization[C]//Proceedings of the SIGGRAPH, San Diego,USA: ACM, 2003: 19-25.

[4] Garland M. Multi resolution modeling: survey & future opportunities[C]//Proceedings of the Eurographics, Granada,Spain: Eurographics Association, 1999: 49-65.

[5] 付鑫, 陈睿, 唐雁. 基于频度中心理论的三维模型简化方法[J]. 计算机科学, 2008, 35(7): 216-218.FU Xin, CHEN Rui, TANG Yan. 3D model simplification algorithm based on degree centrality[J]. Computer Science, 2008,35(7): 216-218.

[6] 刘湘云, 邹北骥. 一种依概率值简化三角网格模型的新算法[J]. 中南大学学报: 自然科学版, 2005, 36(1): 123-127.LIU Xiangyun, ZOU Beiji. A new algorithm for simplying triangle mesh model based on probability[J]. J Cent South Univ:Science and Technology, 2005, 36(1): 123-127.

[7] 冯翔, 周明全. 带纹理的三维模型简化算法[J]. 计算机辅助设计与图形学学报, 2009, 21(6): 842-846, 852.FENG Xiang, ZHOU Mingqun. An algorithm for simplification of 3D models with texture[J]. Journal of Computer-Aided Design & Computer Graphics, 2009, 21(6): 842-846, 852.

[8] 胡于进, 蔡建荣, 凌玲, 等. 基于物理属性与三角形正则度的网格简化算法[J]. 华中科技大学学报: 自然科学版, 2011,39(6): 96-100.HU Yujin, CAI Jianrong, LING Ling. Simplified algorithm of mesh by using physical properties and triangle regularity[J]. J Huazhong Univ of Sci & Tech: Nature Science Edition, 2011,39(6): 96-100.

[9] 卢威, 曾定浩, 潘金贵. 支持外观属性保持的三维网格模型简化[J]. 软件学报, 2009, 20(3): 713-723.LU Wei, ZENG Dinghao, PAN Jingui. Mesh simplification for 3D models with feature-preserving[J]. Journal of Software, 2009,20(3): 713-723.

[10] 李凤霞, 赵邓, 李仲君. 基于外观保持的多分辨率模型生成算法[J]. 系统仿真学报, 2012, 24(1): 62-66.LI Fengxia, ZHAO Deng, LI Zhongjun. Mesh Simplification for 3D models with exterior maintaining[J]. Journal of System Simulation, 2012, 24(1): 62-66.

[11] 陈伟海, 徐鲤鸿, 刘敬猛, 等. 网格简化中基于特征矩阵的二次误差测度算法[J]. 北京航空航天大学学报, 2009, 35(5):572-575.CHEN Weihai, XU Lihong, LIU Jingmeng, et al. Quadric errormetrics formesh simplification based on featurematrix[J].Journal of Beijing University of Aeronautics and Astronautics,2009, 35(5): 572-575.

[12] 杜晓晖, 尹宝才, 孔德慧. 一种边折叠三角网格简化算法[J].计算机工程, 2007, 33(12): 12-15.DU Xiaohui, YIN Baocai, KONG Dehui. Triangle mesh simplification algorithm based on edge collapse[J]. Computer Engineering, 2007, 33(12): 12-15.

[13] Andersson M, Gudmundsson J, Levcopoulos C. Restricted mesh simplification using edge contractions[J]. International Journal of Computational Geometry and Application, 2009, 19(3):247-265.

[14] Kaick Y M, Pedrini H. A comparative evaluation of metrics for fast mesh simplification[J]. Computer Graphics Forum, 2006,25(2): 197-210.

[15] Atlan S, Garland M. Interactive multiresolution editing and display of large terrains[J]. Computer Graphics Forum, 2006,25(2): 211-223.

[16] 宋占峰, 詹振炎, 蒲浩. 基于不规则三角网的视相关细节层次网格化方法研究[J]. 铁道学报, 2003, 25(1): 99-103.SONG Zhanfeng, ZHAN Zhenyan, PU Hao. Study on the method of view-dependent level-of-detail meshing based on triangulated irregular net[J]. Journal of the China Railway Society, 2003, 25(1): 99-103.

[17] 蒲浩, 宋占峰, 詹振炎. 基于约束 Delaunay三角剖分的道路三维建模方法[J]. 华中科技大学学报: 自然科学版, 2005,33(6): 111-113.PU Hao, SONG Zhanfeng, ZHAN Zhenyan. 3D-modelling for roads based on constrained Delaunay triangulation[J] J Huazhong Univ of Sci & Tech: Nature Science Edition, 2005,33(6): 111-113.