基于内禀尺度分量的自适应时频分析方法
程军圣,李海龙,杨宇
(湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082)
近几年来,时频分析方法在信号分析中得到了广泛的应用。典型的时频分析方法有窗口傅里叶变换、小波变换等,经研究发现这些方法缺乏自适应性。为了更方便地分析信号,又提出了自适应性的时频分析方法,例如:经验模态分解方法(Empirical mode decomposition,简称EMD)和局部均值分解方法(Local mean decomposition,简称LMD)。EMD方法[1]是在定义瞬时频率具有物理意义的内禀模态函数(Intrinsic mode function,简称IMF)的基础上,将复杂的多分量信号自适应的分解为若干个IMF分量之和,进一步对每个IMF分量进行Hilbert变换[2]求出瞬时频率和瞬时幅值,从而得到原始信号完整的时频分布。LMD方法[3]将一个单分量的调幅-调频信号看成是其本身的包络信号和一个纯调频信号的乘积,即 PF分量,首先采用极值点获得局部均值函数和包络估计函数,然后在对原始信号不断解调的过程中获得瞬时频率具有物理意义的纯调频信号和相应的包络信号,将纯调频信号和包络信号相乘便可得到一个 PF分量,从而可将复杂信号自适应的分解为若干个PF分量之和[4]。经研究发现EMD方法中采用3次样条线形成上、下包络线时产生过包络、欠包络以及Hilbert变换带来负频率[5]等问题,LMD方法也存在端点效应[6]、频率混淆、由于解调而引起信号突变、计算量大等问题。虽然EMD与LMD方法有各自的优点和缺陷[7],但是它们有一个共同特点,那就是首先采用基于极值点的局部特征尺度参数定义一种瞬时频率具有物理意义的单分量信号(在EMD方法中为IMF分量,在LMD方法中为PF分量),然后据此对信号进行自适应的分解。因此,EMD与LMD方法在提供有效的自适应时频分析方法的同时,也提供了一个很好的自适应时频分析思路,即首先假设任意一个复杂信号由若干个瞬时频率具有物理意义的单分量信号组成,并给出该单分量信号所需要满足的条件[8],然后据此条件对原始信号进行自适应地分解。基于以上的思路,本文作者采用基于极值点的局部特征尺度参数,定义了另一种瞬时频率具有物理意义的单分量信号—内禀尺度分量(Intrinsic scale component,简称ISC),在此基础上提出了一种新的自适应时频分析方法—局部特征尺度分解方法(Local characteristic-scale decomposition,简称LCD),本文将展开对局部特征尺度分解方法的研究。
1 LCD方法
LCD方法假设任何复杂信号由不同的ISC分量组成,任何2个ISC分量之间相互独立,这样任何一个信号x(t)就可以被分解为有限个ISC分量之和。为了定义瞬时频率具有物理意义的ISC分量,考察瞬时频率具有物理意义的典型单分量信号,如调幅信号、调幅-调频信号[9]等,从图1可以看出:在这2种典型信号中相邻2个极值点的时间跨度都无规律可循,但是,它们有一个共同特点,就是图1中的A点和B点相对于时间坐标轴对称。由此,可以给出瞬时频率具有物理意义的单分量信号所满足的条件,并将满足该条件的单分量信号叫做ISC分量。
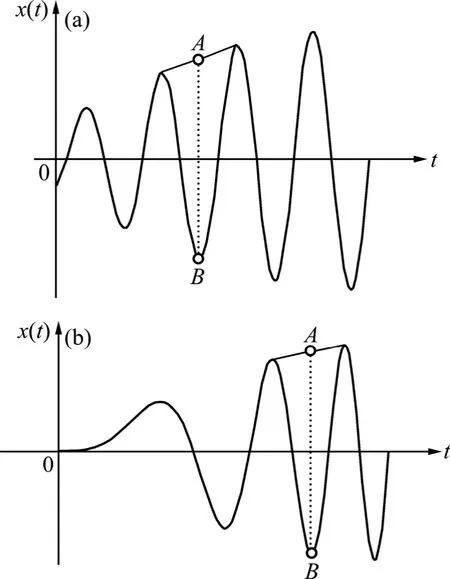
图1 瞬时频率具有物理意义的2种典型信号Fig. 1 Two kinds of typical signals’ instantaneous frequency with physical significance
ISC分量满足以下条件:(1) 在整个数据段内,任意2个极值点之间呈单调性;(2) 在整个数据段内,其极值点为Xk,k=1,2,…,M,各个极值点相对应的时刻为 τk,k=1,2,…,M,由任意 2个极大(小)值点 (τk,Xk)和(τk+2,Xk+2)连接而成的线段在其中间极小(大)值点(τk+1,Xk+1)相对应时刻 τk+1的函数值与该极小(大)值Xk+1的比值关系不变,即,即满足,如图2所示。其中,a∈ (0,1),为常量,典型情况下,a=1/2,例如正弦或余弦信号、调幅信号、调频信号、调幅-调频信号等。
以上2个条件保证了ISC分量任意2个极值点之间具有单一的模态,而且在局部(极值点与相邻的零交叉点之间)吻合标准正弦曲线,因此瞬时频率具有物理意义。

图2 ISC分量满足的条件Fig. 2 Conditions of ISC components needed to meet
对任意信号 x(t)进行局部特征尺度分解,将其分解为若干个ISC分量之和,其步骤如下:
(1) 确定 x(t)的所有极值 Xk,k=1,2,…,M 及其相对应的时刻τk,k=1,2,…,M,并设置参数a,在任意 2个相邻极值点之间对 x(t)进行线性变换,得到
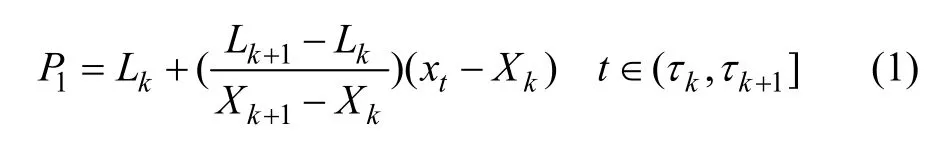
式中:

理想情况下,P1为一个 ISC分量,则 P1为信号x(t)的第1个分量。
(2) 如P1不满足ISC的条件,则将P1作为原始信号重复步骤(1),循环k次,直到得到内禀尺度分量Pk,Pk即为信号x(t)的第1个分量ISC1。
(3) 将 ISC1从 x(t)中分离出来,得到一个新的信号r1,将r1作为原始信号重复步骤(1)和(2),得到x(t)的第2个满足ISC条件的分量ISC2,重复循环n次,得到信号x(t)的n个满足ISC条件的分量,直到rn为一单调函数为止。这样便可以将 x(t)分解为 n个内禀尺度分量ISC和一个单调函数rn之和,即

2 仿真信号分析
考察式(4)所示的仿真信号,其由2个单分量的调制信号组成,时域波形如图3所示。
首先采用LCD方法对此信号进行分解,得到了2个ISC分量和一个余量。从图3可以看出与原信号的各部分有对应关系。因为LCD方法采用分段的形式对任意2个相邻的极值点之间的数据段进行线性变换而实现对整个数据段的分解,这样迭代次数相对减少,并且该方法没用插值拟合技术,不会出现拟合误差。而EMD采用3次样条来拟合极值点形成包络线,会产生拟合误差,在信号的端点处也容易产生拟合误差。所以再不进行端点处理的前提下,LCD方法分解结果的端点效应相对于EMD方法不明显,图3和4说明了LCD方法的有效性。
对上述信号进行EMD分解,由于在EMD分解中,求包络平均是通过对原数据中的极大值点和极小值点分别进行样条插值拟合[10]然后再平均的。在样条插值时,除非数据的2个端点处就是数据的极值点,否则就不能确定端点处的极值点,会在样条插值时产生数据的拟合误差,易产生端点效应,得到的结果如图 4所示,从图4可以看出端点效应比较严重。
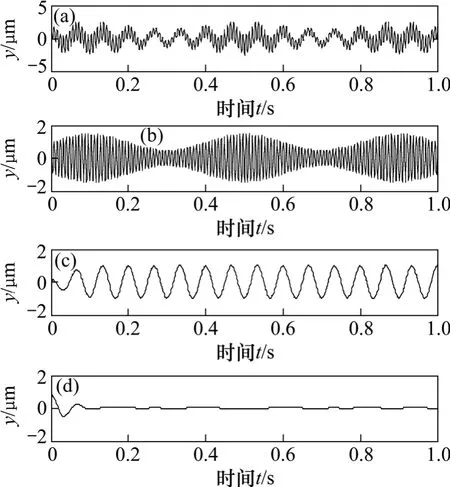
图3 LCD分解结果Fig. 3 LCD decomposition results
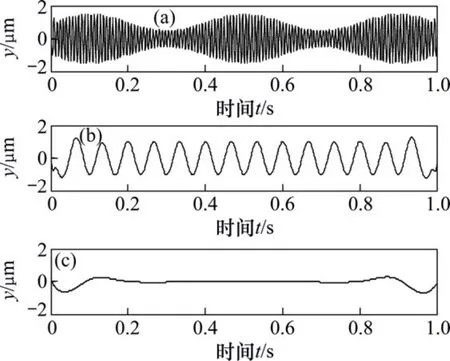
图4 EMD分解结果Fig. 4 EMD decomposition results
为了减弱端点效应对分解结果的影响,采用端点数据延长的方法[11]对图3和4的端点效应进行处理,处理后的结果如图5和6所示。

图5 LCD端点效应处理后的分解结果Fig. 5 End effects processing of LCD and its decomposition results

图6 EMD端点处理后的分解结果Fig. 6 End effects processing of EMD and its decomposition results
对上述信号的分析,可以看出LCD方法的优点:(1) LCD方法是用分段的形式对任意两个相邻的极值点之间的数据段进行线性变换而实现对整个信号的分解,迭代次数减少,没有利用插值拟合技术,不会出现拟合误差,这样该方法产生的端点效应相对不明显。而EMD分解采用3次样条线形成上、下包络线时易产生过包络、欠包络,从而极易引发端点效应[12],上面的例子清晰的说明了这个问题。(2) LCD对信号逐段进行线性变换,避免了整体插值的过程,这样也使其计算量大大减少;而EMD中采用3次样条插值形成上下包络线,再计算包络平均,计算量很大[13],所以LCD的计算效率要高于EMD的计算效率。
3 实验信号分析
将 LCD方法与包络分析法[14-15]相结合应用于齿轮振动加速度信号的分析,首先对振动加速度信号进行LCD分解,得到若干个平稳的ISC分量,然后对包含主要振动信息的高频ISC分量求其包络谱,根据包络谱分析齿轮是否有故障。
在齿轮故障实验台上进行实验,分别采集了裂纹齿轮振动加速度信号和正常齿轮振动加速度信号,实验的齿轮是标准直齿轮,齿轮的转频为20 Hz,采样频率为1 024 Hz。取一裂纹齿轮振动加速度信号,并对其进行LCD分解,如图7所示,取第1个ISC分量进行分析,得到包络谱如图8所示。
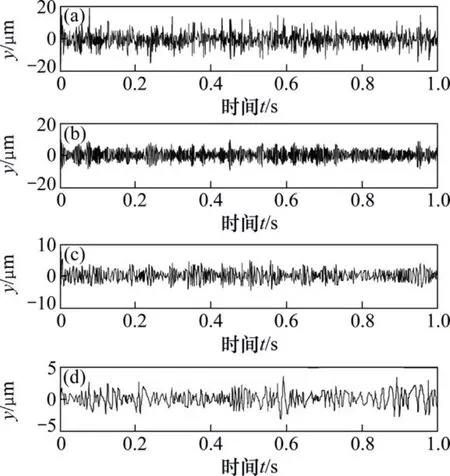
图7 裂纹齿轮信号的LCD分解结果Fig. 7 Signal of crack gear’s LCD decomposition results
从图8 可以清晰地看到在2倍频40 Hz处有明显的谱线,由此可以确定齿轮存在局部故障。
再取一正常齿轮振动加速度信号,并对其进行LCD分解,如图9所示。取第1个ISC分量进行分析,得到包络谱如图10所示。
从图9中第1个ISC分量看不出明显的调幅特性,并且其包络谱图10中没有明显的谱线。所以可以判定齿轮工作正常。
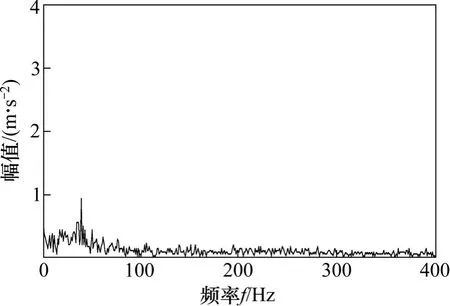
图8 裂纹齿轮ISC1分量的包络谱Fig. 8 ISC1 component’s envelope spectrum for crack gear
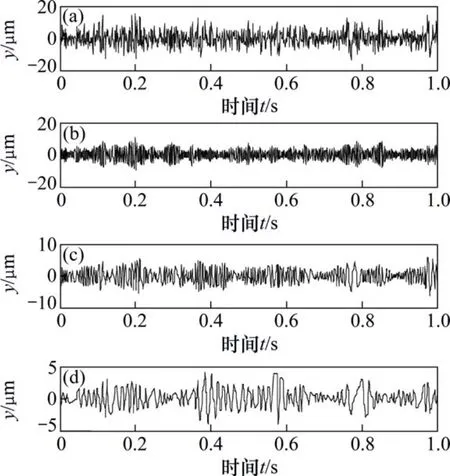
图9 正常齿轮信号的LCD分解结果Fig. 9 Signal of normal gear’s LCD decomposition results
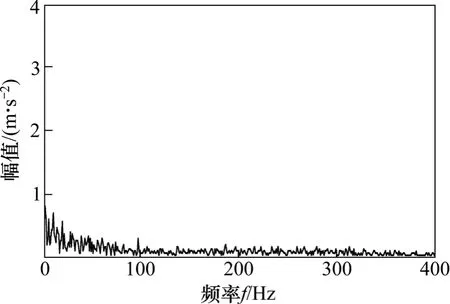
图10 正常齿轮ISC1分量的包络谱Fig. 10 ISC1 component’s envelope spectrum for normal gear
从以上对实验信号的分析中可以看出:LCD方法能自适应的将齿轮实际振动加速度信号分解为若干个ISC分量之和,对ISC分量进行包络分析可得到齿轮故障特征信息,从而正确判断齿轮的工作状态。这说明LCD方法可以有效的应用于齿轮故障诊断。
4 结论
提出了一种新的信号自适应时频分析方法—局部特征尺度分解方法,简称LCD,并用LCD方法对仿真信号和齿轮的实际振动加速度信号进行了分析,从分析结果可以看出 LCD方法能很好地提取各信号的信息特征,这也说明了LCD方法的有效性,并且为机械故障诊断提供新的有效分析手段。
[1] Liu B, Riemenschneider S, Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum[J].Mechanical Systems and Signal Processing, 2006, 20(3):718-734.
[2] Huang N E, SHEN Zheng, Long S R. A new view of nonlinear water waves: The Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31: 417-457.
[3] Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of Royal Society Interface, 2005,2(5): 443-454.
[4] 程军圣, 杨宇, 于德介. 局部均值分解方法及其在齿轮故障诊断中的应用[J]. 振动工程学报, 2009, 22(1): 76-84.CHENG Junshen, YANG Yu, YU Dejie. The local mean decomposition method and its application to gear fault diagnosis[J]. Journal of Vibration Engineering, 2009, 22(1):76-84.
[5] 薛嫚. 总体平均经验模式分解方法的理论研究[D]. 黑龙江:哈尔滨工程大学水声工程学院, 2007: 14-15.XUE Man. Research and application of ensemble empirical mode decomposition principle[D]. Harbin Engineering University,School of Underwater Acoustic Engineering, 2007:14-15.
[6] 程军圣, 张亢, 杨宇. 局部均值分解与经验模式分解的对比研究[J]. 振动与冲击, 2009, 28(5): 13-16.CHENG Junsheng, ZHANG Kang, YANG Yu. A comparison between the local mean decomposition and the empirical mode decomposition method[J]. Journal of Vibration Engineering and Shock, 2009, 28(5): 13-16.
[7] 刘慧婷, 张旻, 程家兴. 基于多项式拟合算法的EMD端点问题的处理[J]. 计算机工程与应用, 2004(16): 84-86.LIU Huiting, ZHANG Min, CHENG Jiaxing. Dealing with the end issue of EMD based on polynomial fitting algorithm[J] .Computer Engineering and Applications, 2004(16): 84-86.
[8] Norden E. Huang, Zheng Shen, Steven R. Long. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society, 1998, 454: 903-995.
[9] Wang W J, Mcfadden P D. Application of wavelets to gearbox vibration signals for fault detection[J]. Journal of Sound and Vibration, 1996, 192(5): 927-939.
[10] Loh C H, Wu T C, Huang N E. Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses[J]. Bulletin of The Seismological Society of America,2001(91): 1339-1357.
[11] 宁静, 诸昌钤, 高品贤, 等. EMD分解中端点数据的延长方法问题研究[J]. 计算机工程与应用, 2011, 47(3): 125-128.NING Jing, ZHU Changqian, GAO Pinxian, et al. Research on extending end data in empirical mode decomposition[J].Computer Engineering and Applications, 2011, 47(3): 125-128.
[12] 林丽, 周霆, 余轮. EMD算法中边界效应处理技术[J]. 计算机工程, 2009, 35(23): 265-268.LIN Li, ZHOU Ting, YU Lun. Edge effect processing technique in EMD algorithm[J]. Computer Engineering, 2009, 35(23):265-268.
[13] 黄大吉, 赵进甲, 苏纪兰. 希尔波特-黄变换的端点延拓[J].海洋学报, 2003, 25(1): l-11.HUANG Daji, ZHAO Jinjia, SU Jilan. Practical implementation of the Hilbert-Huang Transform algorithm[J]. Acta Oceanolgica Sinica, 2003, 25(1): l-11.
[14] 焦卫东, 朱有剑. 基于EMD的轴承故障包络谱分析[J]. 轴承,2009(1): 47-49.JIAO Weidong, ZHU Youjian. Envelope spectrum analysis of bearing fault based on EMD[J]. Bearing, 2009(1): 47-49.
[15] 于德介, 程军圣, 杨宇. 机械故障诊断的 Hilbert-Huang变换方法[M]. 北京: 科学出版社, 2006: 186-191.YU Dejie, CHENG Junshen, YANG Yu. Mechanical fault diagnosis based on Hilbert-Huang transformation[M]. Beijing:Science Press, 2006: 186-191.

