一种基于自适应粒子滤波的多层感知器学习算法

席燕辉 ，叶志成 ，彭辉

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；2. 长沙理工大学 电气与信息工程学院，湖南 长沙，410077；3. 先进控制与智能自动化湖南省工程实验室，湖南 长沙，410083)

多层感知器是一种典型的前馈神经网络，它在时间序列的非线性预测、模式识别与分类、系统建模、动态系统控制等领域得到了广泛的应用。用来训练多层感知器的最常用的学习方法是BP算法，BP算法对于小型的简单网络能够取得较好的效果。随着神经网络变得复杂和训练数据的增加，BP算法的收敛速度减慢，且容易陷入局部极小点等。Iiguni等[1-2]提出用扩展卡尔曼算法(the extended kalman filter, EKF)引入到多层神经网络的学习中。把前馈网络所有权值作为EKF算法的状态，网络输出作为EKF的观测，结果表明，EKF训练算法明显优于BP算法。但EKF训练算法也存在一些难点或问题：噪声统计特性的确定，特别是系统噪声；系统初始状态和初始协方差的设置；一阶线性化处理，可能使得滤波器的性能大为下降，甚至出现发散现象。针对上述问题，很多人提出了许多改进的神经网络算法[3-14]，如无忌卡尔曼滤波算法(UKF)、自适应 UKF算法、进化算法等。de Freitas等[10-14]相继提出了过程噪声可调的自适应 EKF训练算法(EKFQ)和基于粒子滤波(HySIR)的神经网络训练算法，前者通过在线更新过程噪声的统计特性提高EKF的滤波性能，后者使用EKF方法来构造粒子滤波的重要性密度函数，在多层神经网络训练中得到良好的效果。但HySIR算法同样要求准确已知系统噪声统计特性，实际上，对于神经网络状态空间模型，噪声统计参数通常是变化的，而且很难准确获得。由此需要采用自适应方式在线辨识噪声统计特性参数，即利用观测数据进行递推滤波的同时，不断地由滤波本身来判断动态系统是否变化。如果判断发生了变化并把这种变化判别为随机干扰，则可由滤波本身去估计由它产生的模型噪声方差阵,或者当模型噪声方差未知或不准确时，由滤波本身不断地去估计和修正。在实际系统中，量测噪声的统计特性通常可以较精确的获得，而过程噪声的统计特性则很难进行评价，所以本文主要针对过程噪声进行讨论。本文作者采用Jazwinski所提出的序贯最大化可信度更新先验信息的方法来辨识系统的过程噪声[15]，提出了一种在线辨识噪声的自适应粒子滤波(APF)神经网络训练算法。该算法利用粒子滤波进行递推的同时，不断的在线辨识出系统噪声特性，仿真结果表明该方法有效地提高了网络收敛的速度和精度。

1 神经网络状态空间模型

为了把滤波算法引入到多层感知器网络学习中，需要把网络所有的权值看作是系统的状态变量，而网络的输出看成是系统的观测变量，相应的状态空间模型如下：

式中：yk∈Rm为输出量，uk∈Rn为输入量，wk∈Rp为神经网络的权值。非线性函数g(·)使用一个多层感知器来近似(本文采用Sigmoidal激活函数的感知器)。系统的量测噪声 vk和过程噪声 dk为 0均值的高斯噪声，协方差分别为Rk和Qk。系统k时刻状态(网络的权)依赖于k-1时刻网络的权以及系统随机噪声dk，因此，过程噪声dk的变化特性直接决定了系统权的变化。在通常情况下，都假定量测噪声vk和过程噪声dk的协方差Rk和Qk是确定不变的。而实际上，噪声统计特性参数通常是变化的，而且也很难准确获得。由此需要在线辨识系统噪声统计特性来提高滤波精度。

2 噪声估计

噪声辨识的方法有很多，本文采用的是Jazwinski所提出的序贯最大化可信度更新先验信息的方法来辨识系统的过程噪声。该方法认为噪声均值为 0，仅对噪声二阶中心矩(协方差)进行估计。根据贝叶斯理论，可以采用下式来估计噪声Qk：

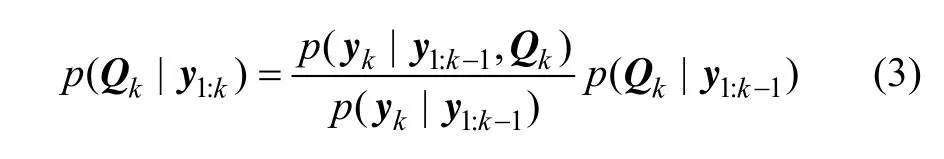
由于没有Qk的先验信息 p (Qk| y1:k)，可以通过最大化可信度密度函数 p (yk| y1:k-1,Qk)来估计Qk，即

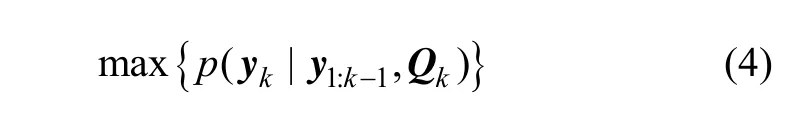
而

其中，1ˆk-w为k-1时刻状态(权)向量wk-1的滤波估计；Pk-1为k-1时刻状态向量wk-1的滤波估计误差的协方差矩阵；H为向量函数()·g的雅克比矩阵，即

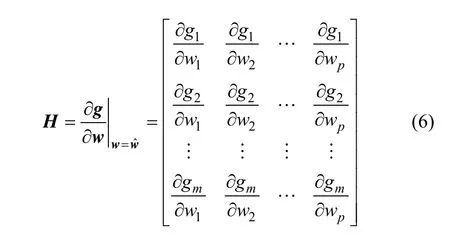
设预测误差ek为当前时刻接收数据yk与基于以前接收数据对当前时刻数据的预测值 E [yk| y1:k-1,Qk]的差，即

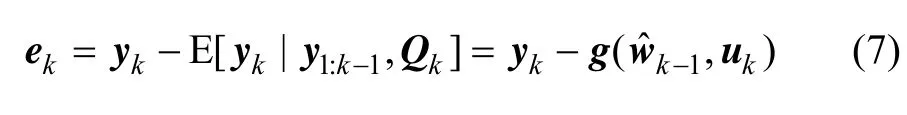
因此，预测误差的概率密度函数为：

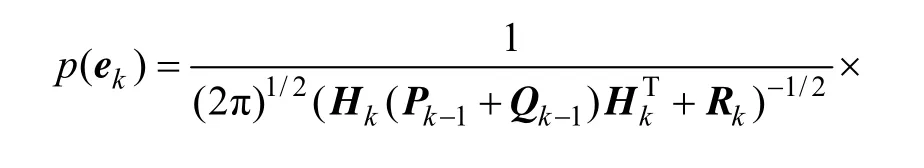
由此可知：k时刻预测观测值yk和预测误差ek都为高斯变量，两者具有相同的方差，只是均值不同，因此，最大化预测误差概率密度函数与最大化可信度概率密度函数(预测概率密度函数)等效。假设系统过程噪声协方差矩阵可用参数qk来描述，即：Qk=qkI。要最大化预测误差概率密度函数p(ek)，即

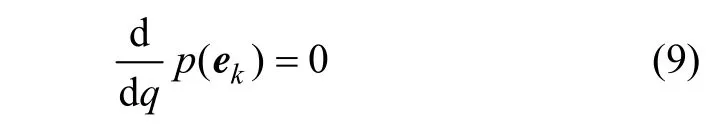
由式(9)可得序列更新qk：

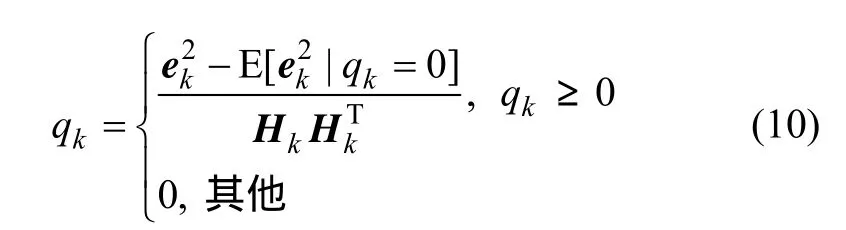
此方法的含义是，每当预测误差的协方差大于理论值时就增加qk，即利用预报残差来修正系统噪声方差Qk，从而提高观测值的可信度。但是此估计器只利用某一时刻的预测误差，因此不具有统计意义，一个更有效的方法是使用多个时刻预测误差的均值来提高估计的准确性。假设有M个时刻(也称窗口)，其预测误差均值

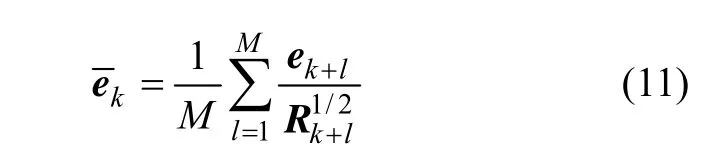
代入式(10)得：

其中：

3 自适应粒子滤波神经网络训练算法

粒子滤波的核心思想是用一组加权的随机样本(粒子)来近似表征状态后验概率密度函数[16-17]，其关键是重要性密度函数的选择。本文用EKF对每个粒子进行更新，将最后得到的近似后验密度作为重要性密度函数，同时用上述的方法更新系统噪声方差，其具体算法步骤如下：

2 0 1 4年5月的梁璐，坐在深圳一处老旧的办公楼内，和几名九零后职场新人一起学习电商之道。1月份还俗的他，没多久便应承下朋友的这份差事，也遂了他“做些实事”的愿望。

步骤1 初始化(k=0)，从网络权先验密度函数中采样N个粒子，并给定初值和系统噪声方差参数q0。

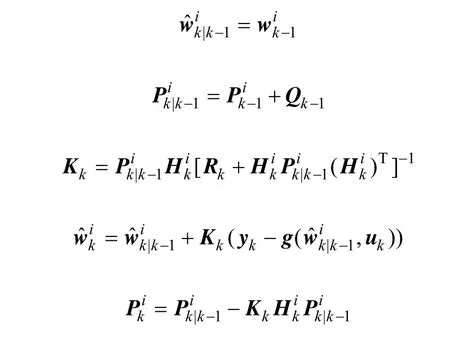
步骤3 按照式(12)计算qk，更新系统噪声协防差矩阵Qk=qkI。

步骤5 计算粒子的权重，并归一化。

步骤6 重采样。

步骤8 令k=k+1，重复步骤2～7，直到循环结束。

4 仿真实验

为验证本文所提算法的有效性，选取了文献[12]中的2类数据进行仿真实验。

4.1 理论模型数据

300组输入输出数据由下列非线性非平稳状态空间模型产生：

其中：ωk和vk分别为零均值，方差为0.01和2sin2(0.1k)的高斯白噪声。实验中，隐含层神经元数由1变到10，输出层为1个线性神经元。网络的初始权值为方差为1的正态分布随机数，状态的初始协方差为10，系统噪声和观测噪声的方差分别为0.01和2，窗口的大小M=10，粒子滤波中粒子数目为500。

图1给出了模型的输入输出数据，图2所示为自适应粒子滤波算法中参数qk。表1给出了4种算法的平均一步预测误差的均方根值，进行了100次独立实验。从仿真结果可以看出，自适应粒子滤波神经网络算法在不同的神经元下都优于传统的算法。

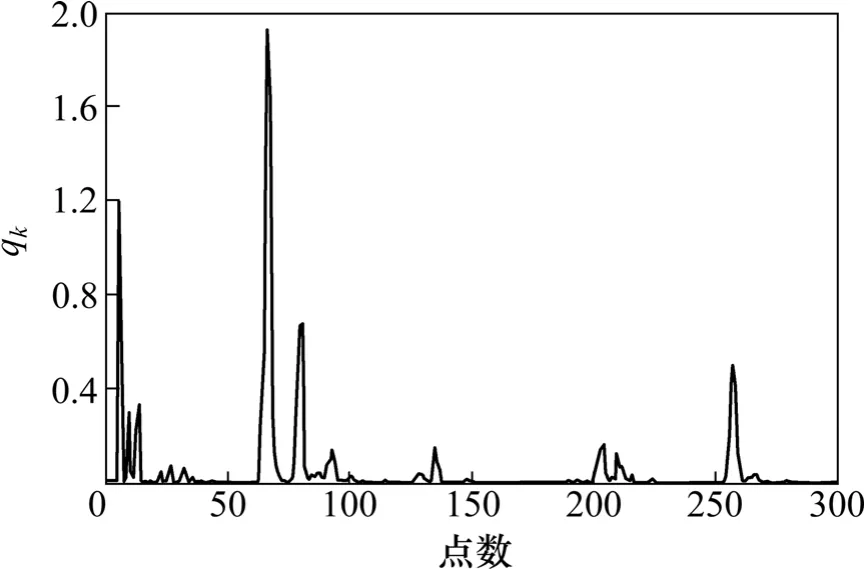
图2 自适应粒子滤波中噪声参数qk与时间的关系Fig.2 Relationship between time and noise parameter qk in APF

表1 各种不同训练算法的预测结果比较Table 1 Performance comparison of all training algorithms

4.2 金融期权模型

选取来自英国富时100指数(FTSE100 index)中期权定价数据，时间跨度为1994-02—1994-12，同样用一个3层感知器来逼近这些数据，隐含层神经元数为6，输出层为1个线性神经元。网络的初始权值为正态分布的随机数，方差为1，状态的初始协方差为10，过程噪声和观测噪声的方差分别为 1×10-5和 1×10-4，窗口的大小M=5，粒子滤波中粒子数目为500，表2(看涨期权)和表3(看跌期权)给出了4种算法的平均一步预测误差的均方根值，进行了100次独立实验。图3和图4所示分别为看涨期权和看跌期权价格的原始数据，图5所示为自适应粒子滤波算法中参数qk(看涨期权：C=3 025)。从仿真结果也可以得出自适应粒子滤波算法的一步预测误差的均方根值要小于其他算法的均方根误差值，但与HySIR算法相比，相差很小。这是因为在此模型中，参数q几乎不随时间变化(波动小)，而且变化的幅度很小(0～3.5×10-6)。

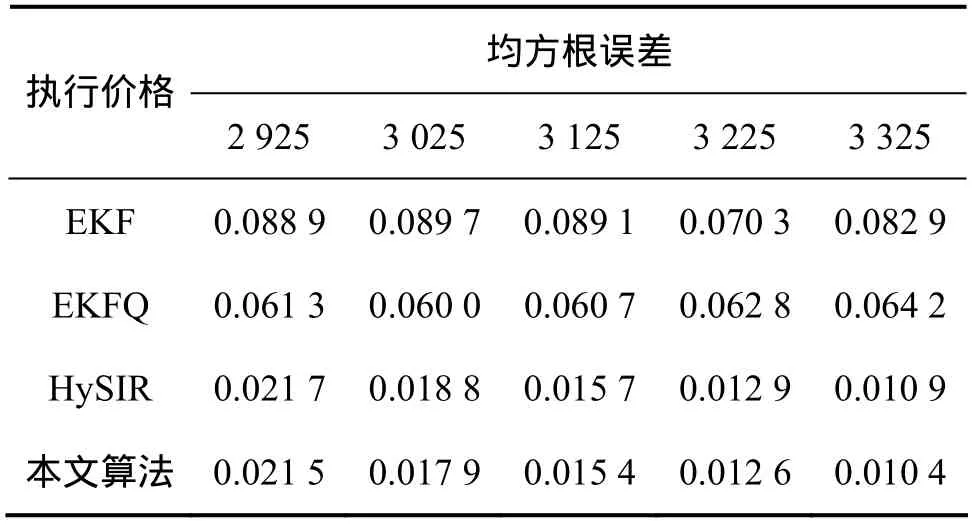
表2 各种不同训练算法的预测结果比较(看涨期权)Table 2 Performance comparison of all training algorithms(Call options)

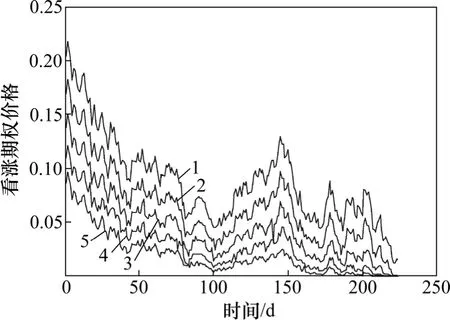
图3 看涨期权原始数据Fig.3 Original data of call options

图4 看跌期权原始数据Fig.4 Original data of put options

图5 自适应粒子滤波中噪声参数qk与时间的关系(C=3 025)Fig.5 Relationship between time and noise parameter qk in APF

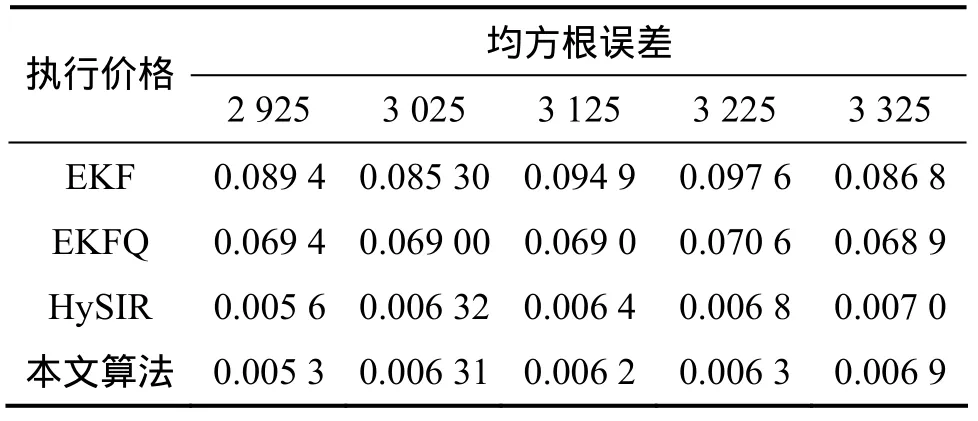
表3 各种不同训练算法的预测结果比较(看跌期权)Table 3 Performance comparison of all training algorithms(Put options)

5 结论

(1) 针对系统过程噪声未知的非线性神经网络状态空间模型，本文作者提出了一种自适应的粒子滤波神经网络训练算法。该算法利用粒子滤波进行滤波的同时，不断地应用序贯更新先验信息的序贯可信度最大化方法在线估计系统噪声方差，从而实现了对系统噪声统计特性的实时估计。

(2) 分析和仿真结果表明，该训练算法有效的降低均方根误差，具有更好的鲁棒性和训练质量。

(3) 这种算法中窗口的选择还有待进一步研究。

[1] Iiguni Y, Sakai H, Tokumaru H. A real-time learning algorithm for a multilayered neural network based on the extended Kalman filter[J]. IEEE Transactions on Signal Processing, 1992, 40(4):959-966.

[2] Singhal S, Wu L. Training multilayer perceptrons with the extended Kalman algorithm[C]//Advance in Neural Information Processing Systems 1. California: Morgan Kaufmann Publishers Inc, 1989: 133-140.

[3] 宋彦坡, 彭小奇. 一种结构自适应神经网络及其训练方法[J].控制与决策, 2010, 25(8): 1255-1268.SONG Yanpo, PENG Xiaoqi. New structure adapting neural network and its training method[J]. Control and Decision, 2010,25(8): 1255-1268.

[4] ZHU Yan, LU Yingrong, LI Qian. MW-OBS: An improved pruning method for topology design of neural network[J].Tsinghua Science and Technology, 2006, 11(3): 307-312.

[5] Konstantios P F. Biological engineering application of feedforward neural networks design and parameterized by genetic algorithms[J]. Neural Network, 2005, 18(7): 934-950.

[6] Haralambos S, Alex A, Stefanos M, et al. A new algorithm for developing dynamic radial basis function neural network models based on generic algorithm[J]. Computers and Chemical Engineering, 2004, 28(1): 209-217.

[7] YU Jianbo, WANG Shijin, XI Lifeng. Evolving artificial neural networks using and improved PSO and DPSO[J].Neurocomputing, 2008, 71(4/5/6):1054-1060.

[8] ZHAN Ronghui, WAN Jianwei. Neural network-aided adaptive unscented Kalman filter for nonlinear state estimation[J]. IEEE Signal Processing Letters, 2006, 13(7): 445-448.

[9] 钟华, 金国平, 郑林华. 基于扩展卡尔曼滤波的FLANN网络学习算法[J]. 信号处理, 2009, 25(10): 1555-1559.ZHONG Hua, JIN Guoping, ZHENG Lin-hua. Learning algorithm based on extended Kalman filter for functional link artificial neural networks[J]. Signal Processing, 2009, 25(10):1555-1559.

[10] de Freitas J F G, Niranjan M, Gee A H. Hierarchichal Bayesian-Kalman models for regularisation and ARD in sequential learning[J]. Neural Computation, 2000, 12(4), 933-953.

[11] de Freitas J F G , Niranjan M, Gee A H, et al. Sequential monte carlo methods to train neural network models[J]. Neural Computation, 2000, 12(4): 955-993.

[12] de Freitas J F G , Niranjan M, Gee A H, et al. Sequential monte carlo methods for optimisation of neural network models[R].England: Cambridge University, 1998: 1-33.

[13] de Freitas J F G, Niranjan M, Gee A H. Regularisation in sequential learning algorithms[C]//Jordan M I, Kearns M J, Solla S A. Advances in Neural Information Processing Systems 10.Massachusetts: Massachusetts Instituite of Technology Press,1998.

[14] de Freitas J F G, Niranjan M, Gee A H. Hybrid sequential monte carlo/Kalman methods to training neural networks in non-stationary environments[C]//IEEE International Conference on Acoustics and Signal Processing. Arizona, USA, 1999:1057-1060.

[15] Jazwinski A H. Adaptive filtering[J]. Automatica, 1969, 5(4):475-485.

[16] Kitagawa G. Monte Carlo filter and smoother for non-Gaussian nonlinear state space model[J]. Journal of Computational and Graphical Statistics, 1996, 5(1): 1-25.

[17] Kitagawa G. A self-organizing state space model[J]. Journal of the American Statistical Association, 1998, 93(443): 1203-1215.