基于四元数的6R串联机器人运动学逆解应用

陈 爱，冯 桑，何 春，陆 晓

（广东工业大学，广东广州 510006）

0 前言

空间6R机械手的运动学逆解是空间机构学中最难的问题之一，曾被Freudenstein喻为机构运动学中的“珠穆朗玛峰”[1]。传统的逆运动学求解方法具有一定的局限性，比如D-H 法的矩阵运算中，需要对进行大量的“0”元素以及矩阵求逆运算，计算冗余繁杂；文献[2]利用特定机器人几何构型特点求得机器人运动学逆解的解析式，但其运算过程需要大量人工参与，不具通用性，求解困难，而且涉及多解和奇异性等问题，不易实现实时在线控制[2]。

四元数法是基于旋量理论（Screw Theory）的一种算法，可以在一个全局坐标系下建立各个刚体位置以及刚体运动的描述[2]。四元数法的物理意义在于其可以表征刚体变换时瞬时欧拉轴和所需的转角。四元数法与欧拉方程相比，具有计算量小、精度高[2]，且不会出现奇异现象等特点[2-3]。

1 四元数（quaternion）及普吕克坐标系（Plücker coordinate）

1.1 四元数

四元数由一个实数单位和三个虚数单位组成，可以看作是拓展后的复数，通常写成

式（1）中，q0，q1，q2，q3均为实数，i，j，k 服从以下运算规律：

单位四元数（unit quaternion）是模为1 的四元数，可以将其写成：

（1）单位四元数的共轭

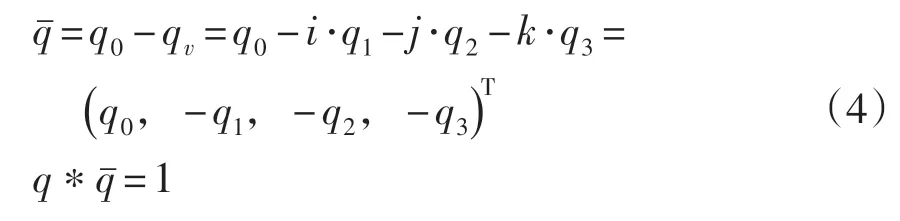
其中：*为四元数乘法。

（2）单位对偶四元数

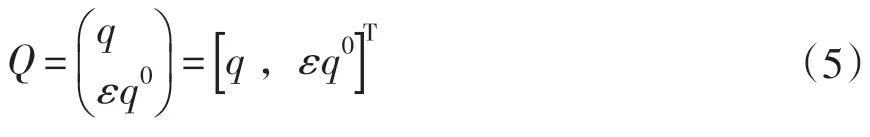
其共轭

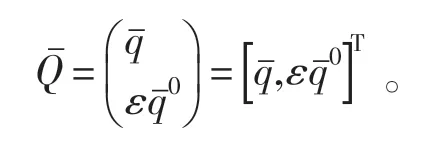
1.2 普吕克坐标系

三维空间直线在普吕克坐标系下描述为：

其中：d 为直线的单位方向向量；m=p×d ，p 为直线上任意一点的坐标向量。

采用普吕克坐标系表示直线后，直线由其方向向量d 和直线上任意一点p 构成，并且直线方程与该直线上的点的具体位置无关。因此在普吕克坐标系下表示直线，有利于简化6R机器人各连杆的结构。

那么两直线的交点P 可以用以下方程求得

1.3 普吕克坐标系下刚体运动的描述

对于给定型号的机器人，其初始位置时各轴心线的方向矢量均为已知。轴心线线上的点可以通过几何关系获得。普吕克坐标系下的直线Lpi可以看作是一个特殊的对偶四元数，其旋转部分和向量部分的是不均为零的纯旋转为了满足四元数运算，将普吕克坐标下的直线扩展为8 维表示，即6R工业机器人各关节轴线：

i=1～6，为6R机器人第i 个旋转轴。

2 单位四元数在6R 串联机器人运动学正解中的应用

本文采用对偶四元数法，利用6R 串联机器人的末端三轴交于一点的几何特点，以及四元数的物理意义，容易求得6R 串联机器人运动学正解。

2.1 末端位置求解

由于6R机器人末端三轴心线交于一点（称为腕关节点，wrist）才能有封闭解（如图1）。为了简化计算，笔者求第4、5轴的交点。因此，腕关节点坐标Pw为：

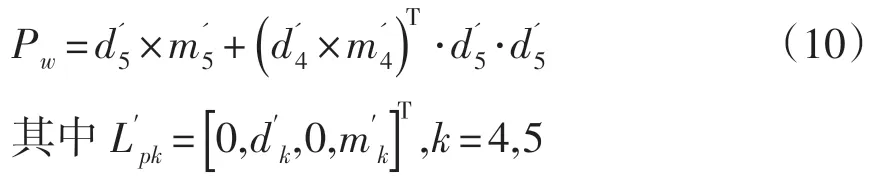
图1 6R串联机器人结构示意图

2.2 末端姿态求解

6R 机器人的末端姿态通常用欧拉角表示，机器人工具坐标系在各关节旋转后与旋转前变换过程中所产生的x、y和z轴的旋转变换。

根据几何变换关系可得：

设坐标系通过绕z，y，x 轴旋转角度γ，β，α 到坐标系，其对应的四元数为qz，qy，qx，则[8]：

其中qx，qy，qz分别表示绕x，y，z 旋转的四元数。

反之同理可以得到用四元数N0，N1，N2，N3来表示欧拉角，则可以得到：

6R 机器人运动学正解由末端的位置和姿态构成，由上述公式可以求得机器人运动学正解。

3 6R 串联机器人运动学逆解（Inverse Kinematic）

6R 串联机器人运动学逆解的求解是一个难题。与运动学正解相反，运动学逆解是根据机器人末端姿态求解机器人关节角的问题。TSAI 等[1]利用高维逼近分析逆运动学，推出了不同结构的各种6R 机器人最多只有16 解的结论。然而一般6R 串联机器人的逆解解析的表达式往往很复杂，这给快速精确计算运动学逆解带来了困难。在笛卡尔坐标系下，倪振松[1]等，将刚体运动用双四元数描述，但其构造Dixon结式进行消元求解，得到一元十六次方程，但其求解方程过程较为复杂，对计算机资源配置要求非常高。而Paden-Kahan法由于其自身局限性，因此通常将串联机器人的运动学逆解分解为多个Paden-Kahan 子问题进行求解。但在其空间几何关系转换过程中，计算量庞大，增加了整个计算过程的计算量。

3.1 求解机器人第6轴方向

带下标_ik 的符号表示运动学逆解中的变量，下同。

从而得到了机器人关节点的坐标值pw_ik。

3.2 求解串联机器人各个关节角

前三个关节角可以通过几何关系求得：

图2 平面二杆机构示意图

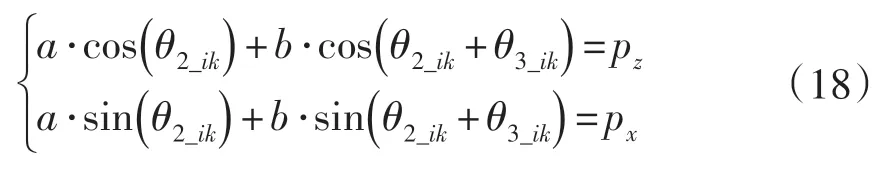
其中：a，b 分别表示平面二杆机构的杆长，θi为关节i的转角角度，当杆长已知的情况下，通过上述方程组可以求得方程组的解为：

根据几何关系，d5始终和d6、d4垂直，即：

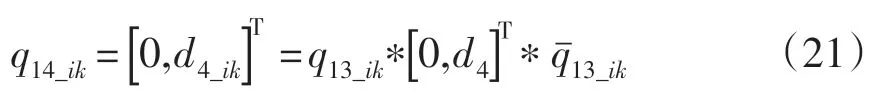
该等式等号左边是一个常数值；等号右边的物理意义是：第5关节的轴心线绕第4关节轴心线旋转θ4后得到的结果。等式中唯一的变量是θ4_ik，根据等式很容易求得θ4_ik的值，等式中唯一的变量是θ4_ik，根据等式很容易求得θ4_ik的值。

同理：由于q16已知，通过以下等式

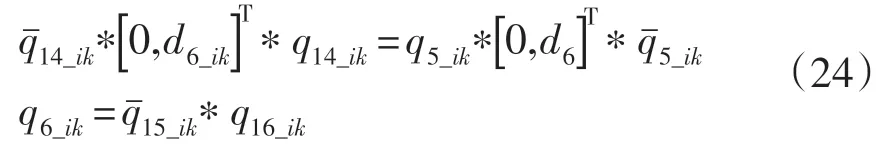
图3 机器人模型图

分别可以求得θ5_ik，θ6_ik。

至此6R串联机器人运动学逆解全部求得。

4 四元数法求解6R串联机器人运动学实例

本文针对如图3 所示的机器人，进行四元数法的6R串联机器人的运动学仿真。该机器人几何尺寸如表1。

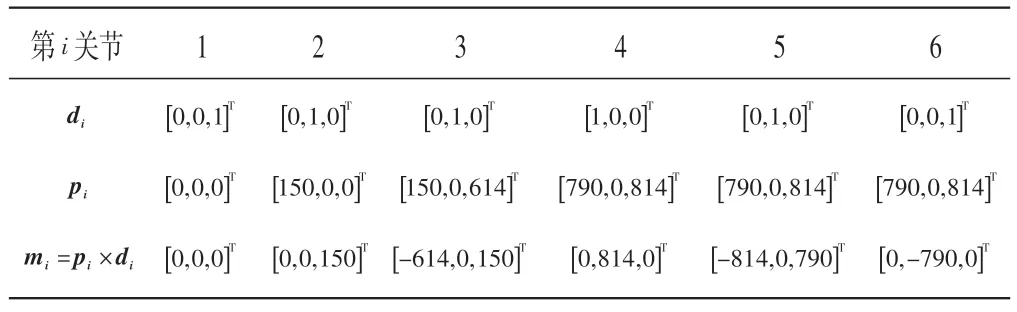
表1 6R串联机器人基本参数

4.1 正解

根据表格中的机器人的基本参数，由公式（3），可以得到各轴心线旋转的单位四元数描述：

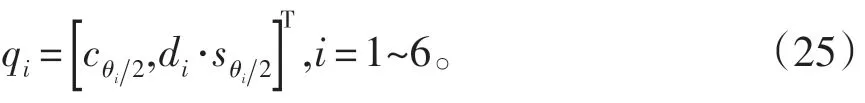
再将公式（25）代入到公式（5）可以得到绕各轴心线变换的单位对偶四元数描述：

然后将表格中数据带入到公式（8），可以得到各个轴心线在普吕克坐标系下的直线方程：

将（26）（27）代入到公式（10）、（11）和公式（14），可以得到6R 串联机器人的运动学正解，即机器人末端位置和姿态。

4.2 机器人运动学逆解

在已知机器人末端点位置PE_ik以及欧拉角αik，βik，γik的情况下，由公式（13）可以得到：

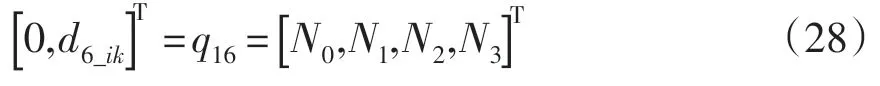
可以得到串联机器人的6 个关节角θi（i=1，2，3，4，5，6）。

5 计算仿真

本文利用Matlab/robot toolbox工具箱建立机器人运动学模型，再对基于四元数法的6R串联机器人的运动学逆解进行了计算仿真。任意给定6 个关节的旋转角度θi后，利用Matlab/Simulink 模型对运动学正解进行仿真，得到机器人末端的位置坐标（Position）及末端的欧拉角（EulerAngle），再将其输入到运动学逆解模块（Inverse Kinematic），得到8个运动学逆解结果。过程及结果如图4所示。

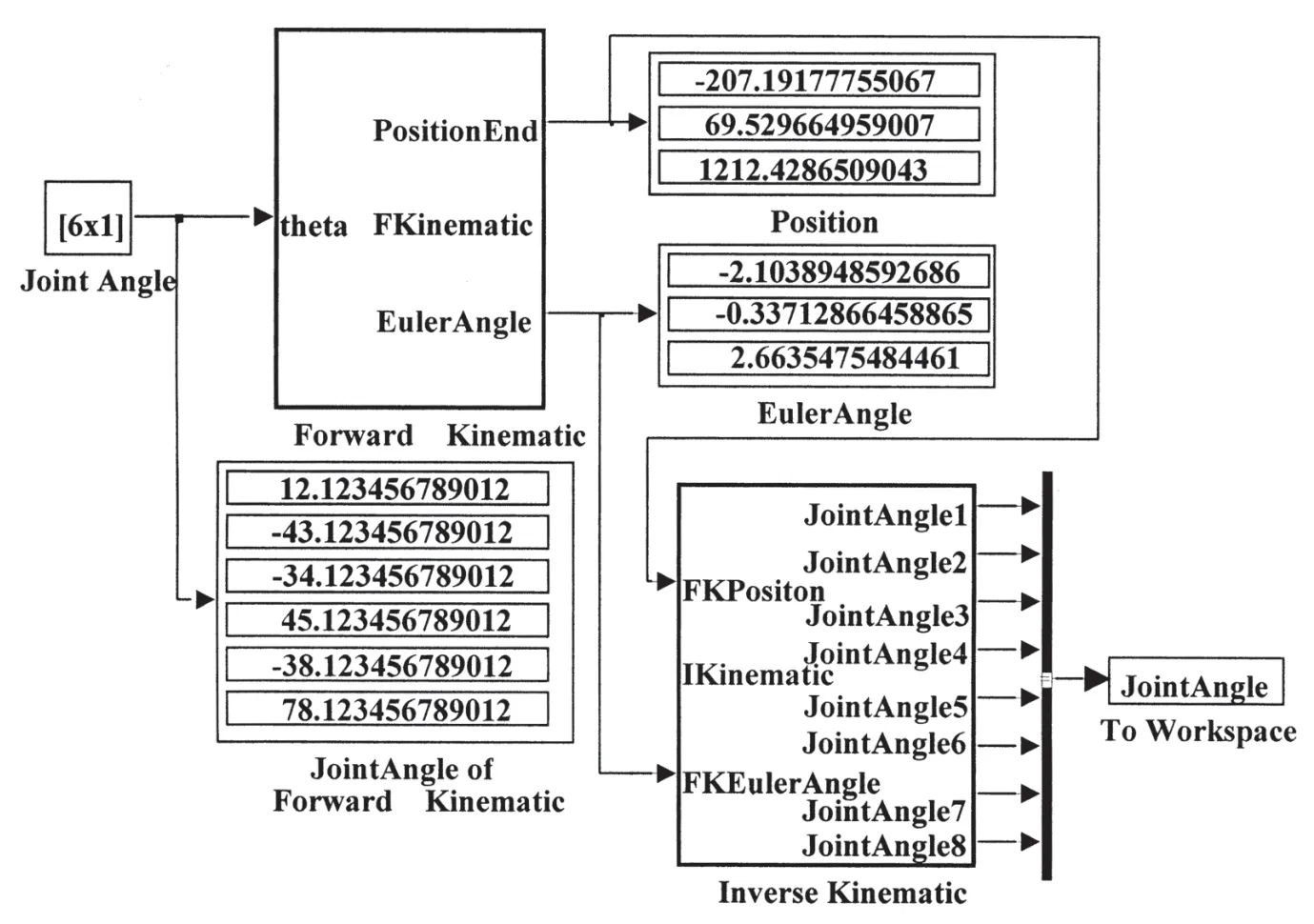
图4 串联机器人运动学Simulink仿真模型

将经过四元数正解后得到的机器人末端执行器的姿态代入模型进行运动学逆解模型进行求解，得到8 组运动学逆解（如表2）。从表中数据可以看出，在误差允许的范围内，第1 组数据和输入的数据完全一样。在Matlab 中计算，该组数据的计算精度完全满足工程应用的需要。

并利用Matlab/robot toolbox建立的机器人运动学模型对该8 组运动学逆解进行姿态仿真，得到图5中的8个机器人姿态。

表2 6R机器人8组运动学逆解

6 结论

将超复数形式的四元数以及对偶四元数应用于6R 串联机构的运动学正逆解分析的数学建模，用基于普吕克坐标系的直线描述串联机构的连杆，避免机构繁琐的D-H法描述，物理意义简洁明了。与D-H法相比，四元数中每一个元素都有很强的物理意义和计算意义，避免无效计算，占用计算机资源，影响着计算速度。

将运动学正解中点的旋转变换转化成变换后的直线的交点，脱离了具体的各连杆的具体位置的计算。

在运动学逆解中，与传统D-H 法通过求解矩阵的逆，再进行矩阵乘法计算，最后解方程。四元素求共轭，只需将虚部正负号改变即刻，计算复杂度极其小。

D-H 法中，两个4×4 矩阵A 和B 相乘得到矩阵C，一般共需要进行7×16=112 次加法或乘法运算；而四元数法中，两个四元数相乘运算，一般共需要进行7×4=28 次加法或乘法运算。从理论上，四元数的计算量也明显小于矩阵的计算量。

四元数法直接得到各个关节旋转角度的一元一次方程或者一元二次方程组，其计算复杂度为O（1），理论上计算复杂度大大降低。

四元数法大大简化了计算过程，提高了计算效率和精度，便于机器人控制的实时性，在实际工程应用中具有很强的实际意义。

采用四元数法，可以统一机器人的运动学中的位置和姿态[1]，即在同一个坐标系就可以完全描述6R机器人的运动学的正逆解。

四元数法除了可以描述转动副外，还可以描述移动或者螺旋运动。因此本文研究的四元数法还可以推广到螺旋副或者移动副的运动机构中，比如四元数用在第4 轴为滚珠丝杠花键轴的SCARA机器人的运动学的数学建模中。

图5 6R机器人运动学8组逆解位姿

［1］Freudenstein F.Kinematics：past，present and future［J］.Mechanism and Machine Theory，1973，8（2）：151-161.

［2］李发忠，赵德安，马从国.FANUC_M-6iB型机器人运动学逆解研究［J］.机械设计与制造，2008（10）：174-176.

［3］于艳秋，王品，廖启征.一般6R机器人的位置反解与运 动 仿 真［J］.中 国 机 械 工 程，2003（24）：2130-2132.

［4］Emre Sariyildiz，Eray Cakiray and Hakan Temeltas.A comparative study of three inverse kinematic methods of serial industrial robot manipulators in the screw theory framework ［J］.International Journal of Advanced Robotic Systems，2011（8）：9-24.

［5］Yurong Nan，Panfeng Wu.A New Method for the Inverse Kinematics of 6-DOF Manipulator Based on Dual Quaternion［J］.Advances in Mechanical and Electronic Engineering Lecture Notes in Electrical Engineering，2012（176）：295-302.

［6］AHN Jin-su，CHUNG Won-jee，JUNG Chang-doo.Realization of orientation interpolation of 6-axis articulated robot using quaternion［J］.J.Cent.South Univ，2012（19）：3407-3414.

［7］程国采.四元数法及其应用［M］.长沙：国防科技大学出版社，1991.

［8］E.Sariyildiz，H.Temeltas，Solution of Inverse Kinematic Problem for Serial Robot Using Dual Quaternions and Plücker Coordinates［A］.IEEE/ASME International Conference on Advanced Intelligent Mechatronics［C］.Suntec Convention and Exhibition Center Singapore，July 14-17，2009.

［9］TSAI L W，MORGAN A.Solving the kinematics of the most general six and five-degree-of-freedom manipulators by continuation methods［J］.Mechanism and Machine Theory，1985，107（2）：189-200.

［10］倪振松，廖启征，魏世民，等.空间6R 机器人位置反解的对偶四元数法［J］.机械工程学报，2009（11）：25-29.

［11］Li Jing，Wang Huinan，Liu Haiying.Dual Quaternion Curve Interpolation Algorithm for Formation Satellites［J］.Transactions of Nanjing University of Aeronautics&Astronautics，2012，29（1）.