磁流变液矩形夹层板的动力特性分析

张 冲，鲁刘磊

（1.广州城建职业学院建筑工程技术系，广东广州 510925）；2.暨南大学重大工程灾害与控制教育部重点实验室，广东广州 510632）

0 引言

随着工业材料的发展，出现了磁流变液、电流变液、压电陶瓷等一批智能材料。其中磁流变液的特点更为突出，磁流变液在不加磁场时为可流动的牛顿液体，在磁场作用下，其特性发生急剧变化，由流体经粘弹性体、粘弹性-塑性体等变化为固体，其屈服强度随外加磁场的增加而增加，移去磁场之后，又恢复其流动特性，整个过程是在毫秒量级的时间内完成[1-4]。基于这些特性，磁流变液被越来越多地用于结构的半主动振动控制。近年来，大多研究对象都只是针对夹层梁结构，而对于磁流变液应用于夹层板的研究很少[5]。

本文针对工程中常见的夹层结构，通过理论分析与实例计算研究了磁流变液四边简支矩形夹层板结构在不同磁场作用下的动力特性变化，分析了磁流变液对夹层板结构动力特性的控制效果及影响。

1 磁流变液矩形夹层板的运动微分方程

1.1 基本假设

磁流变液矩形夹层板示意图如图1 所示。夹层板的上下表面层为各向同性弹性材料，夹层为磁流变液。本文仅研究上层板与下层板等厚的夹层板结构。由于磁流变液具有一定的粘弹性特点，仅考虑其剪切作用，因此本文在经典夹层板理论的基础上采用如下假设：

图1 磁流变液夹层板坐标及几何尺寸

（1）材料服从于Hooke定律；

（2）表板在发生弯曲变形时遵守直法线假设，且各层分界面间无相对滑移；

（3）夹心沿板面方向不承受荷载，夹心中面法线在变形后仍为直线；

（4）不考虑表板阻尼，只考虑芯层阻尼效应，并以复刚度形式表述芯层阻尼特性；

（5）不考虑面内转动惯量的影响。

1.2 运动微分方程的建立及分析

基于上述假设，夹层板中任意一点的位移为：

上述各式中各符号意义：ui，vi，wi（i=1，2，3）分别表示上表层、夹心以及下表层的点沿x，y 和z 方向的位移；u，v，w 分别表示夹层矩形板中面上的点沿x，y 和z 方向的位移；h0表示上下表层中面间的距离；φx，φy分别表示夹心中面法线在xz 和yz 平面内的转角。材料的几何方程为：

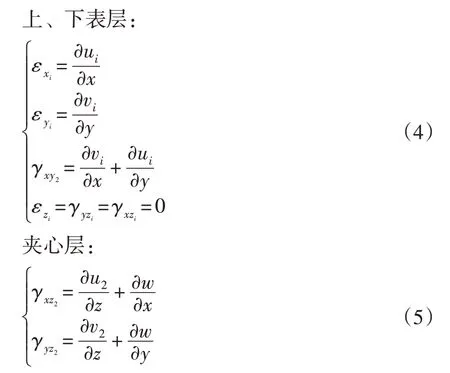
上述式中：εxi，εyi，εzi，γxyi，γxzi，γyzi（i=1，2，3）分别表示上表层、夹心层、下表层的应变分量。将（1）-（3）式代入（4）和（5）得：

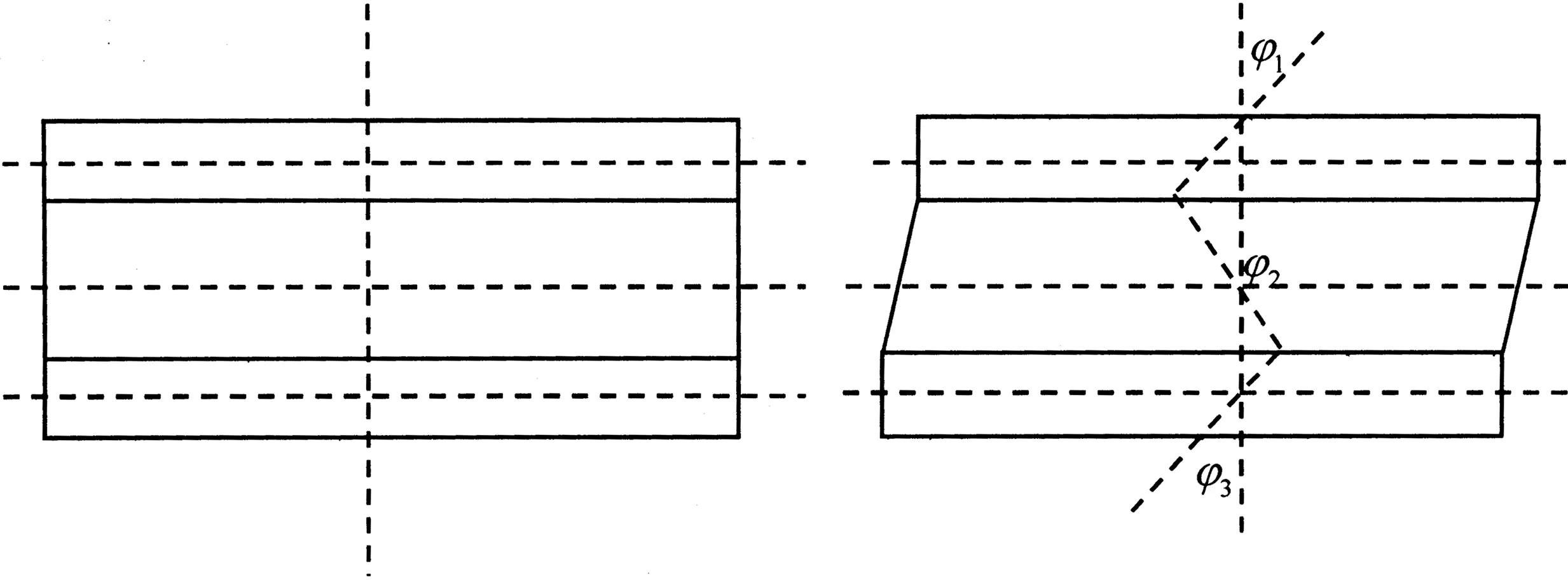
图2 夹层板变形前后示意图

将（6）-（8）式代入下述Hooke定律：

其中σx0，σy0，τxy0表示夹层矩形板中面内的应力分量；σxi，σyi，τxyi，τxz，（i=1，2，3）表示上表层、夹心层、下表层的应力分量；E、v为表层材料的弹性模量和泊松比；G2表示夹心层的剪切模量。根据弹性应变能公式：

本文仅考虑上下表层板均为薄板的情况，上层板和下层板的应变能可写为：

本文基于能量法研究磁流变液夹层板运动微分方程，根据Hamilton原理可知：

其中U为结构总势能，T为结构的总动能，W为外力所做的功。

将式（15）-（18）代入（19）可得：

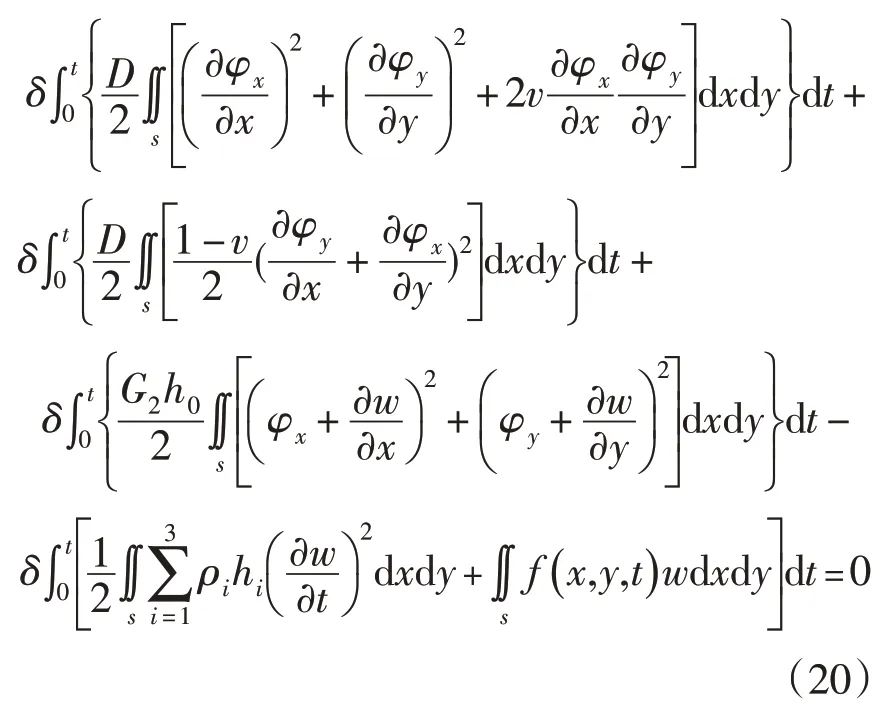
可求得（20）式中分别对w、φx、φy的奥氏方程[6]：

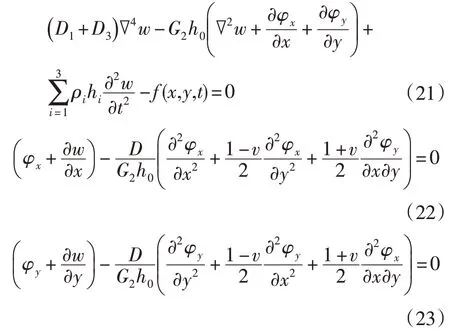
（21）-（23）式便是夹层板结构的运动微分方程。由于本文仅讨论夹层板的自由振动，则f（x，y，t）=0，式（21）可写为：

[7]的解法，假设：

（25）式代入（22）、（23）式中，可得

将（25）、（26）式代入（24）式，有：

薄板自由振动时，设γ（x，y，t）：

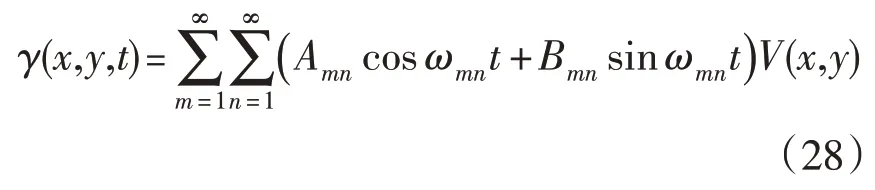
将（28）式代入（27）式：

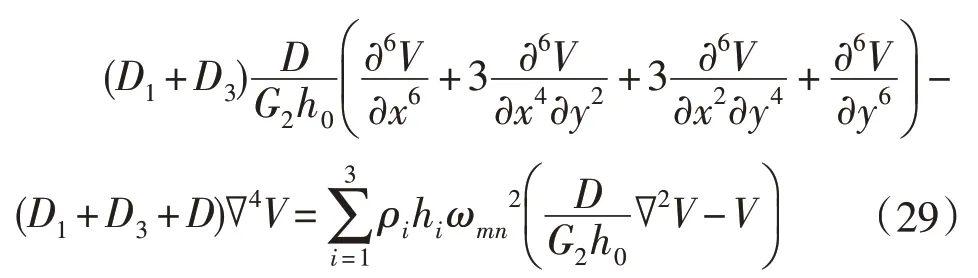
对于四边简支夹层板，边界条件为：

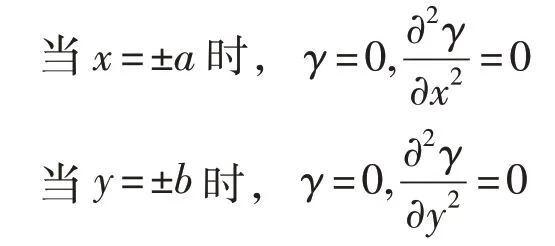
因此根据（28）式可设：

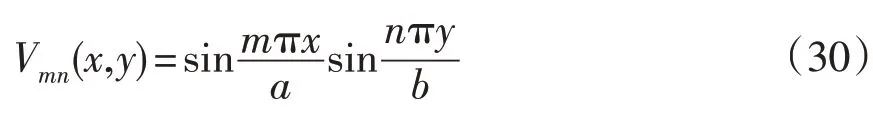
将（30）代入（29）可得结构的固有频率为：

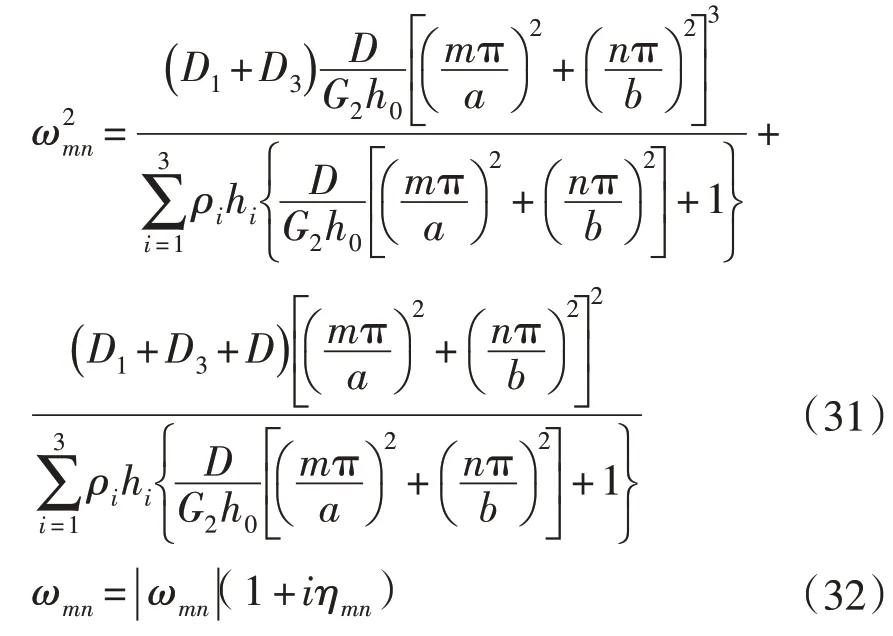
由于所考虑的夹心层为磁流变液，代入的夹心层的剪切模量为磁流变液的复剪切模量，因此还可以得到结构的损耗因子为：

3 理论与有限元计算结果比较

本文对四边简支磁流变矩形夹层板模型进行了理论与有限元计算，本文研究对象尺寸：夹层板：200×200×3.53（mm3），其中上表层、磁流变夹层、下表层的厚度分别为0.765 mm，2 mm，0.765 mm。上下表层弹性模量为70 GPa，密度为2 800 kg/m3，泊松比为0.3；磁流变夹层密度为3 450 kg/m3，泊松比0.3，磁场分为5 种：0 Oe、500 Oe、1 000 Oe、1 500 Oe、2 000 Oe；磁流变层的复剪切模量可根据西安交通大学的Qing Sun等人[9]通过实验测得并拟合出与磁场之间的一组非线性关系来进行计算。

表1 理论计算结果

表2 有限元计算结果

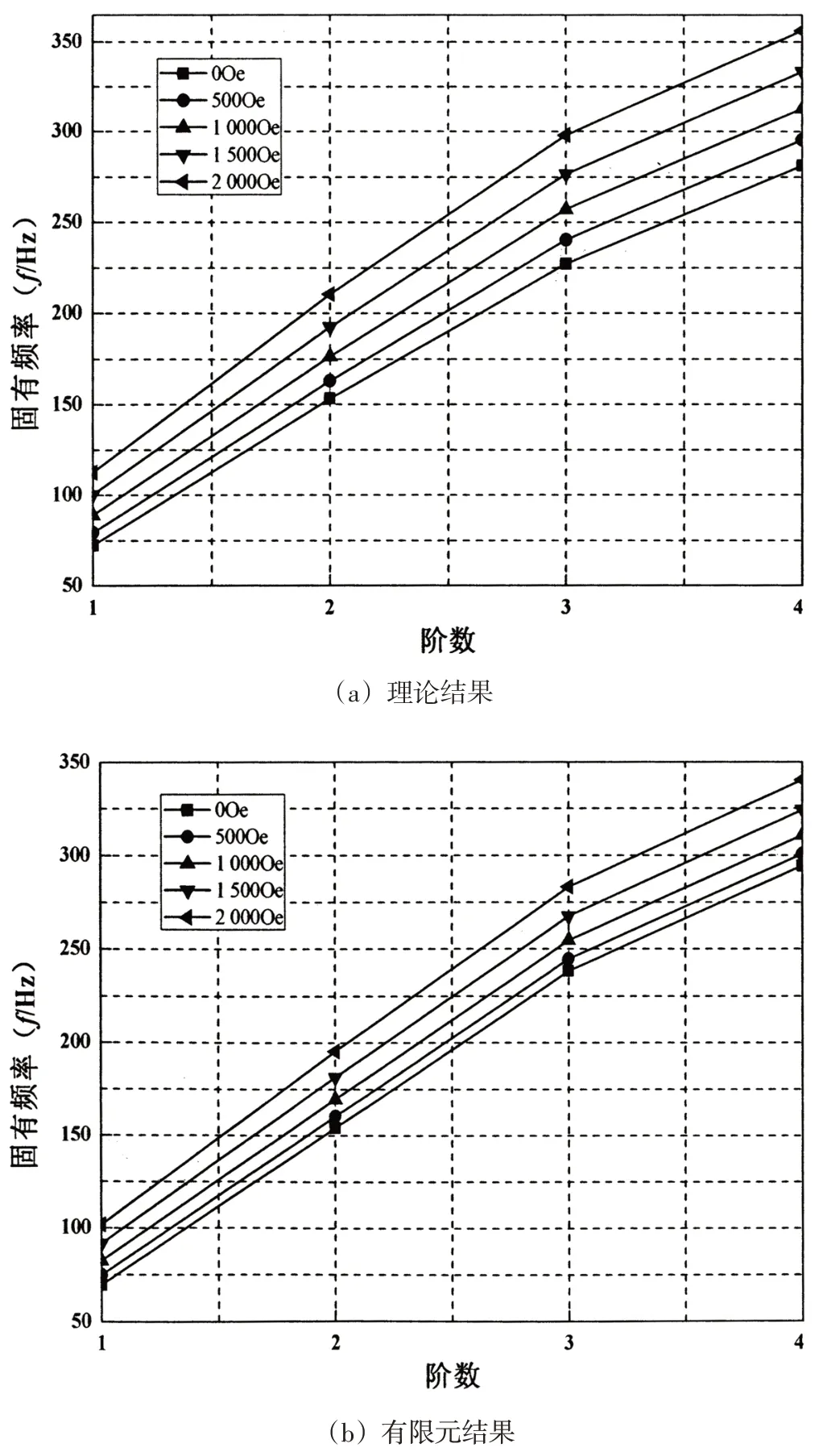
图3 不同外加磁场作用下固有频率变化曲线图

采用上面计算模型尺寸在ANSYS 中利用Solid45 与Visco89 单元[10]分别模拟磁流变液夹层板的上下层板和夹心，并通过计算分析夹层板的振动特性。通过理论与有限元计算分别得到此处磁流变矩形夹层板的固有频率与损耗因子见表1 和表2。

由图3 与图4 可知：理论计算与有限元分析所得计算结果吻合较好。同时也表明：当磁场强度增加，磁流变液矩形夹层板的各阶固有频率均逐渐增大，说明磁流变液的夹层板结构在磁场的作用下，整个结构的刚度和阻尼增大，使结构的共振频率和损耗因子随之增大。而在同一磁场作用下，随着模态阶数的增大，夹层板的固有频率增大，结构的损耗因子减小。

4 结论

（1）通过本文推导的磁流变液夹层板的固有频率与损耗因子计算式计算所得结果与有限元模拟计算结果吻合较好。

（2）在外加磁场的作用下，结构固有频率随着磁场强度的增加而增加，结构阻尼因子也随之增大，这说明磁流变液夹层板振动在外加磁场的作用下得到有效抑制。在相同磁场的作用下，夹层板的低阶模态损耗因子大于高阶模态损耗因子，表明磁流变液夹层板在外加磁场的作用下，对低频振动有较好的抑制效果。

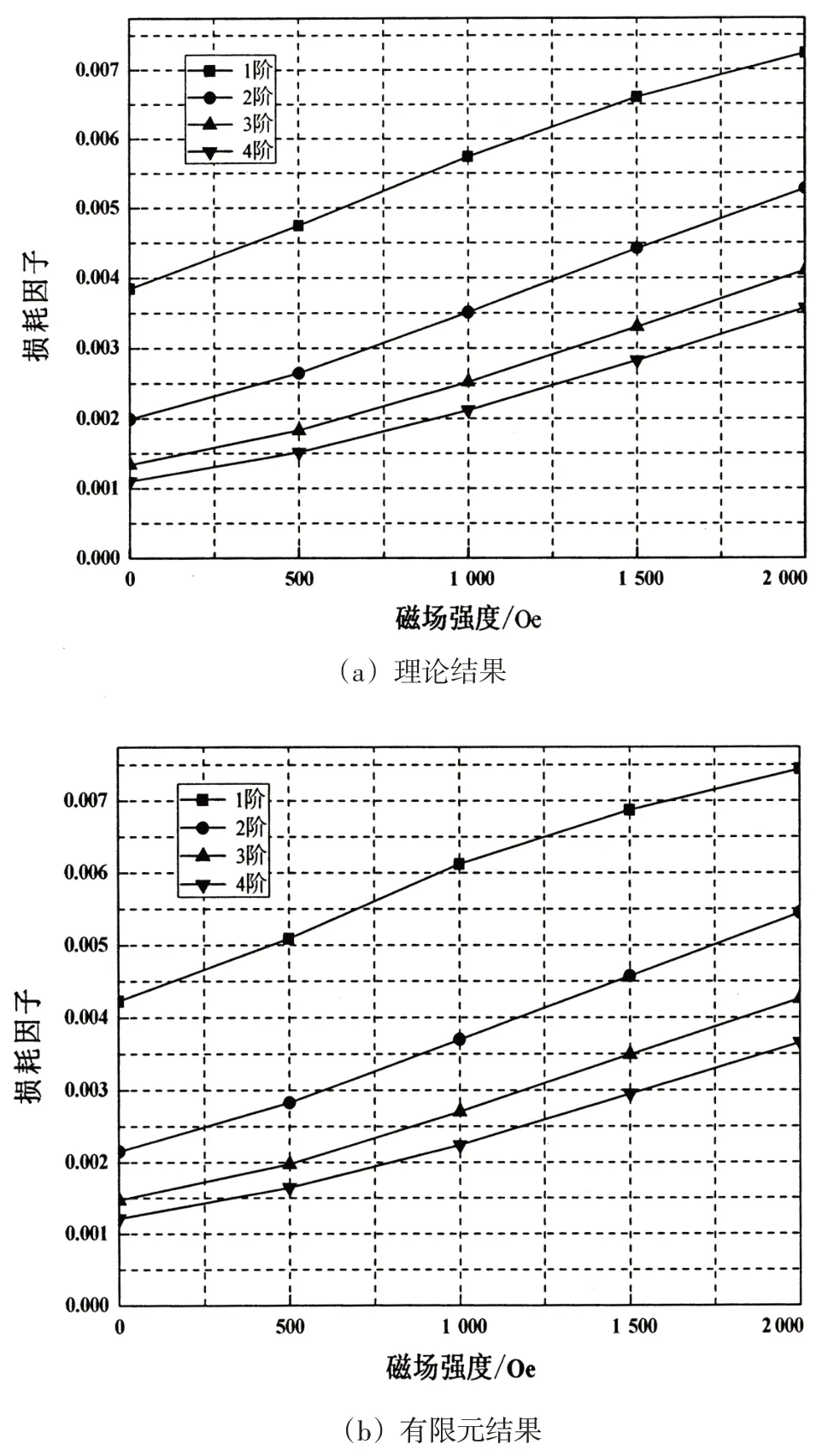
图4 结构阻尼损耗因子随磁场强度变化曲线图

参考文献：

［1］Shulman Z P，Kordonsky W，Zaltsgendler E A.Structure，physical properties andynamics of magnetorheological suspensions ［J］.International journal of multiphase flow，1986，12（6）：935-955.

［2］Kordonsky W.Magnetorheological effect as a base of new devices and technologies［J］.Journal of magnetism and magnetic materials，1993（122）：395-398.

［3］Ginder，J M，Davis L C.Shear stress in magnetorheological fluids［J］.Applied physics letters，1994，65（1）：3410-3412.

［4］Kordonsky W.Static yield stress in magnetorheological fluid ［J］.International journal of modern physics B，2001（15）：1082-1085.

［5］J Snamina.Optimal location of an active segment of magnetorheological fluid layer in a sandwich plate ［A］.Carpathian Control Conference（ICCC），2011：362-365.

［6］老大中.变分法基础［M］.北京：国防工业出版社，2007.

［7］刘人怀，吴建成.夹层矩形板的非线性振动［J］.中国科学：A辑，1991（10）：1075-1086.

［8］徐芝纶.弹性力学：下册［M］.北京：高等教育出版社，2006.

［9］Sun Q，Zhou J X，Zhang L.An adaptive beam model and dynamic characteristics of magnetorheological materials ［J］.Journal of sound and vibration，2003（261）：465-481.

［10］张挣鑫，刘黔会，黄方林.一种在ANSYS 中模拟磁流变液的方法［J］.贵州大学学报，2011（04）：109-113.