基于MATLAB与Pro/E码垛机器人动力学分析*

廖玉城，曾小宁

（广东省机械研究所，广东广州 510635）

0 引言

随着企业劳动力成本不断上升，现代企业纷纷对现有生产方式进行自动化改造，许多搬运、物料的码垛堆放等都需要以机械替代人工。因此码垛机器人的研究应用具有很大的价值[1]。计算机器人完成特定的任务时各轴所需要的力矩，通常通过解机器人逆运动学方程求得。由于解逆运动学方程比较复杂，给开发工业机器人造成了一定的难度。本文介绍了Pro/E软件在分析码垛机器人动力学领域的应用。码垛机器人在完成典型任务时由已知的运动轨迹，通过Pro/E机构分析模拟求得机器人各输入轴的运动参数，然后用这些运动参数作为各轴伺服电机的驱动参数，模拟仿真机器人的运动，以求得机器人各轴的力矩。

1 码垛机器人结构分析及运动学建模

1.1 码垛机器人结构分析

码垛机器人机构简图如图1所示。

图1 码垛机器人机构简图

本机器人共有4 个自由度，其中Ⅰ轴绕竖直轴（z轴）在水平面（xy平面）内转动的转动由电机经减速机直接驱动，它使末端点的轨迹为一个旋转体；大臂绕Ⅱ轴做俯仰运动，由水平安装的电机径减速机直接驱动；小臂绕Ⅲ轴的运动，由电机的转动经曲柄、拉杆转化为小臂的绕Ⅲ轴转动；末端执行器绕Ⅳ轴的转动由电机经减速机直接驱动。此外由于该机器人采用双平行四边形结构，使得末端执行器中心轴线始终保持竖直[2]。

1.2 机器人运动学建模

首先如图2 所示建立机器人的D-H 后置坐标系。根据图2 所示列出后置坐标系的机器人D-H参数表，如表1所示。

图2 码垛机器人机构简图

表1 机器人的D-H 参表

相邻两连杆之间的齐次变幻矩阵通式为：

把表1的数据代入（1）式得：

末端连杆相对基坐标系的位姿变矩阵：

其中：ci=cos（θi），si=sin（θi）（下同）。

此外，由图1 可知机器人的末端执行器与末端连杆的几何关系，根据式（6）求得机器人末端执行器相对基坐标系的位姿变幻矩阵：

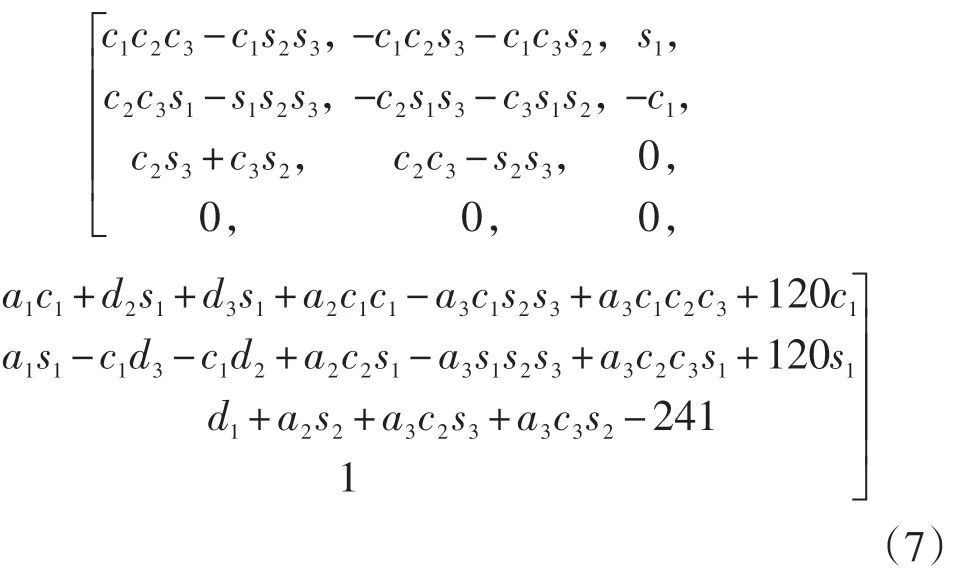
由（7）式可得机器人工作空间的参数方程，其中关节变量θ1、θ2、θ3变化范围由表1给出：

1.3 机器人工作空间

为了能直观地观看到机器人的工作空间，根据式（8），在不考虑机械干涉的条件下，使用MATLAB对机器人工作空间参数方程编程[3]，求解其工作空间三维图，如图3～5所示。

图3 机器人工作空间三维图

图4 机器人工作空间在xy面投影图

2 模拟仿真机器人完成典型任务

2.1 任务假设条件

（1）升降行程200 mm 平移行程500 mm（如图6）；

（2）周期要求：1 800 包/h，即30 包/min，2 s一个来回；

（3）负载20 kg。

2.2 时间规划

根据任务假设条件制定如表2 所示，单个行程进行时间规划：上升时间0～0.4 s、平移时间0.3～0.8 s，下降时间0.7～1 s。

图5 机器人工作空间在xz面投影图

图6 行程

表2 机器人运动时间参表

2.3 计算末端执行器的相对位移

计算公式如下所示

由式（9）、（10）、（11）、（12）算得末端执行点运动轨迹如图7所示。

图7 运动轨迹

2.4 选择工作区域

结合机器人工作空间（图5）和完成典型任务时机器人末端的工作轨迹选择如图8 所示工作区域。

图8 工作区域

其中各点坐标分别为A（1 050，-250，590）、B（1 050，-250，790）、C（1 050，250，790）、D（1 050，250，590）。

所以末端执行器的绝对位移为：

图9 Ⅰ轴位移、速度、加速度图

2.5 运动仿真分析

根据机器人末端运动轨迹由Pro/E机构分析模块求出Ⅰ、Ⅱ、Ⅲ轴完成典型任务时的运动参数如图9、图10、图11所示。

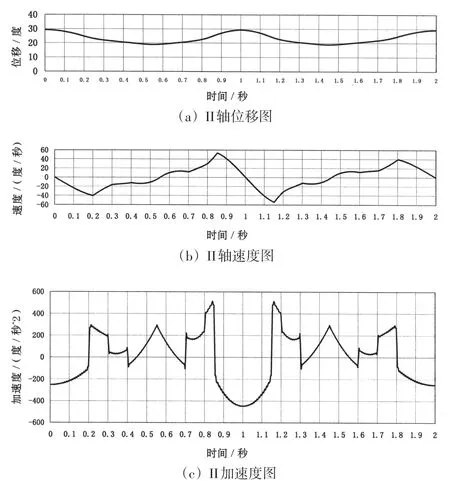
图10 Ⅱ轴位移、速度、加速度图

图11 Ⅲ轴位移、速度、加速度图

把运动参数作为各轴伺服电机的驱动参数，模拟仿真机器人的运动，求得机器人Ⅰ、Ⅱ、Ⅲ轴的力矩如图12、13、14所示。

图12 Ⅰ轴力矩图

图13 Ⅱ轴力矩图

图14 Ⅲ轴力矩图

3 结束语

本文针对完成典型任务时机器人各轴电机、减速机的选择校核的前期力矩计算进行了详细仿真分析，为进一步开发码垛机器人提供了精确的数据。通过MATLAB 计算机器人运动空间，进行运动规划。利用Pro/E强大的建模能力建立机器人的3D模型，并用其机构分析模块对机器人进行动力学分析，由Ⅰ、Ⅱ、Ⅲ轴运动参数求得各轴力矩。

［1］毕胜.国内外工业机器人的发展现状［J］.机械工程师，2008（7）：5-7.

［2］蔡自兴.机器人学［M］.北京：清华大学出版社，2000.

［3］王智兴，樊文欣，张保成，等.基于Matlab 的工业机器人运动学分析与仿真［J］.机电工程，2012（01）：33-37.