Electro-osmotic flow of a second-grade fluid in a porous microchannel subject to an AC electric field*

MISRA J. C.

Department of Mathematics, Institute of Technical Education and Research, Siksha O Anusandhan University, Bhubaneswar, India, E-mail:misrajc@gmail.com

CHANDRA S.

Department of Physics, Sabang S. K. Mahavidyalaya, Vidyasagar University, Midnapore, India

Electro-osmotic flow of a second-grade fluid in a porous microchannel subject to an AC electric field*

MISRA J. C.

Department of Mathematics, Institute of Technical Education and Research, Siksha O Anusandhan University, Bhubaneswar, India, E-mail:misrajc@gmail.com

CHANDRA S.

Department of Physics, Sabang S. K. Mahavidyalaya, Vidyasagar University, Midnapore, India

(Received May 17, 2012, Revised August 7, 2012)

Studies on electro-osmotic flows of various types of fluids in microchannel are of great importance owing to their multifold applications in the transport of liquids, particularly when the ionized liquid flows with respect to a charged surface in the presence of an external electric field. In the case of viscoelastic fluids, the volumetric flow rate differs significantly from that of Newtonian fluids, even when the flow takes place under the same pressure gradient and the same electric field. With this end in view, this paper is devoted to a study concerning the flow pattern of an electro-osmotic flow in a porous microchannel, which is under the action of an alternating electric field. The influence of various rheological and electro-osmotic parameters, e.g., the Reynolds number, Debye-Huckel parameter, shape factor and fluid viscoelasticity on the kinematics of the fluid, has been investigated for a secondgrade viscoelastic fluid. The problem is first treated by using analytical methods, but the quantitative estimates are obtained numerically with the help of the software MATHEMATICA. The results presented here are applicable to the cases where the channel height is much greater than the thickness of the electrical double layer comprising the Stern and diffuse layers. The study reveals that a larger value of the Debye-Huckel parameter creates sharper profile near the wall and also that the velocity of electro-osmotic flow increases as the permeability of the porous microchannel is enhanced. The study further shows that the electro-osmotic flow dominates at lower values of Reynolds number. The results presented here will be quite useful to validate the observations of experimental investigations on the characteristics of electro-osmotic flows and also the results of complex numerical models that are necessary to deal with more realistic situations, where electro-osmotic flows come into the picture, as in blood flow in the micro-circulatory system subject to an electric field.

electrical double layer, Debye length, second-grade fluid, Ionic energy

Introduction

In recent years microfluidics has emerged as an important branch of fluid mechanics. It has occupied a central position in scientific research and has profuse applications not only in engineering and technology, but also in various branches of science, including physiological and medical sciences. Studies on electroosmotic flow in microchannels have been receiving growing interest of researchers in recent years, because of their wide range of applications in many biomedical lab-on-a-chip devices to transport liquids in narrow confinements like sample injection, in the investigation of bio-chemical reactions and in the process of species separation[1-3]. Owing to the developments in micro-fabrication technologies, there has been an urgent need of research on various aspects of miniaturized fluidic systems in order that they can be utilized in a better way for drug delivery, DNA analysis/sequencing systems as well as in the improvement of biological/chemical agent detection sensors.

When a solid surface comes in contact with an aqueous solution of an electrolyte, a structure is formed that comprises a layer of charges of one polarity on the solid side and a layer of charges of opposite polarity on the liquid side of the solid-liquid interface. This phenomenon is known as the Electrical Double Layer (EDL). In order to resolve problems arising out of highly charged double layers, Stern suggested the consideration of an additional internal layer, where the ions are strongly bound.

The Stern layer is formed in the immediate vicinity of the wall with charges opposite to that of the wall and has a typical thickness of one ionic diameter. The ions within the Stern layer are attracted towards the wall with very strong electrostatic forces. But the ions in the outer diffuse layer are less associated and when these free ions experience a force due to the influence of an external electric field, there occurs a bulk motion of the liquid. This type of flow is termed as electro-osmotic flow.

The concept of electro-osmosis has been established experimentally. Several studies on electro-osmosis in microchannels were carried out by some researchers in the recent past[4-7]. Different aspects of electro-osmotic flow in microchannels were investigated by them. All these studies were, however, confined to simple Newtonian fluids. But the flow behavior of a non-Newtonian fluid is of greater interest in many areas of science and technology, including physiology and medicine. Many physiological fluids such as blood, saliva and DNA solutions have been found to be viscoelastic in nature. It is now well known that changes due to different diseases or surgical interventions can be readily identified, considering blood viscoelasticity as a useful clinical parameter. Tang et al.[8]studied the electro-osmotic flow of a non-Newtonian viscous fluid described by the power law model, using the lattice Boltzmann method. Zhao et al.[9]presented a detailed account of studying the effect of dynamic viscosity on the velocity of the electro-osmotic flow of power-law fluids.

Analysis, prediction and simulation of the behaviour of viscoelastic fluids by the use of Newtonian fluid models have been made in the past and they also have been adopted in many industries. But the flow behavior of viscoelastic fluids exhibits wide departure from that of Newtonian fluids. Various non-Newtonian models have been tried by several investigators to explain the complex behavior of viscoelastic fluids. Among them the second grade fluid models have become quite popular. One of the reasons for their popularity is that it has been possible to derive analytical solutions of different problems by adopting the second-grade fluid model and to explore thereby different characteristics of viscoelastic fluids. From the analytical solutions it is also possible to derive various information by using the method of parametric variation.

There is another more important reason for considering second-grade viscoelastic fluid model in preference to other non-Newtonian fluid models. In a recent communication by Misra et al.[I0]it has been mentioned that the second-grade fluid model is compatible with the principles of thermodynamics. Moreover, the specific Helmholtz free energy is minimum in the equilibrium state of the fluid. This is owing to the fact that for a second-grade fluid, all of the following three conditions are met simultaneously whereµrepresents the fluid viscosity coefficient and a1,a2are normal stress moduli. It is worthwhile to emphasize that as a1＜0, the fluid exhibits an anomalous behavior, even if the two other conditions are satisfied and therefore, that sort of fluid model is not suitable for use in any study of rheological fluids.

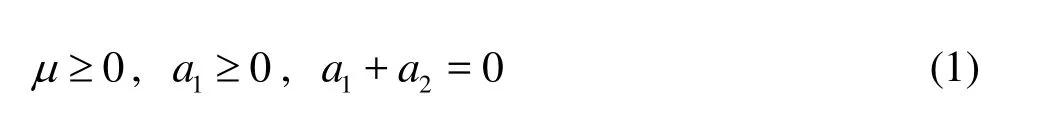
It may further be mentioned that all porous media are stable both mechanically and chemically. Poroelastic and poroviscoelastic media possess the characteristics of porosity and permeability both. By utilizing the porosity factor, it is possible to control the fluid flow[10].

Due to inherent analytical difficulties introduced by more complex constitutive equations, studies of non-Newtonian fluids have been limited to simple inelastic fluid models, such as the power-law model. Influences of viscosity index and electro-kinetic effects on the velocity of a third-grade fluid between microparallel plates were demonstrated by Akgul and Pakdemirli[11]. Dhinakaran et al.[12]presented a solution for a viscoelastic fluid model using the Phan-Thien-Tanner model. Some different aspects of electro-osmotic flow of a viscoelastic fluid in a channel was studied by Misra et al.[13]who also illustrated the applicability of their theoretical analysis to physiological fluid dynamics. But all these studies were limited to the steady case of electro-osmotic flow, where the external electric field was of DC nature, which requires extremely large voltages for producing significant electro-kinetic forces for a controlled transport of the fluid. To maintain controlled micro-bio-fluidic transport, a periodic electric field is better than a DC electric field in multiple ways. Moreover, in the study of some pathological situations as well as in various medical treatment methods, studies on flows in porous channels find significant applications. But all the investigations referred to above are not suitable to depict the exact behavioral pattern of fluid flow through a porous channel.

The present study is motivated towards investigating the flow behavior of a second-grade viscoelastic fluid between two porous plates executing oscillatory motion, under the influence of electro-kinetic forces. In this study, an AC electric field is considered and for the sake of generality, the frequency of the oscillatory plates and that of the electric field are considered to be different. By adopting appropriate constitutive equations, a mathematical analysis has been presented with the purpose of examining the effect of the viscoelastic parameter in the ionized motion of the viscoelastic fluid. Analytical solutions are derived and the derived expressions have been computed numerically for aspecific situation. The numerical estimates obtained on the basis of our computational work, for different physical quantities of special interest are presented graphically. The results will be highly beneficial for validating the results of complex numerical models required for dealing with more realistic situations and also for establishing related experimental observations.

1. The model and its analysis

The constitutive equation of an incompressible second-grade fluid is of the form[14]

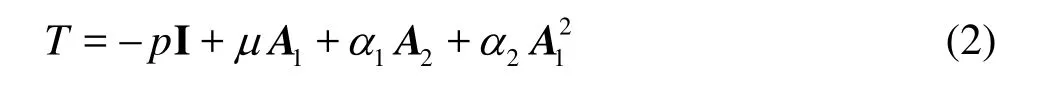
where T is the Cauchy stress tensor,pis the pressure,-pIdenotes the indeterminate spherical stress andu,α1and α2are measurable material constants which denote, respectively, the viscosity, elasticity and cross-viscosity. These material constants can be determined from viscometric flows for any real fluid. A1and A2are the Rivlin-Ericksen tensors[14]and they denote, respectively, the rate of strain and acceleration.A1and A2are defined as

whereu is the velocity vector,∇, the gradient operator,T, the transpose andd/dtthe material time derivative.

The basic equations governing the motion of an incompressible fluid are

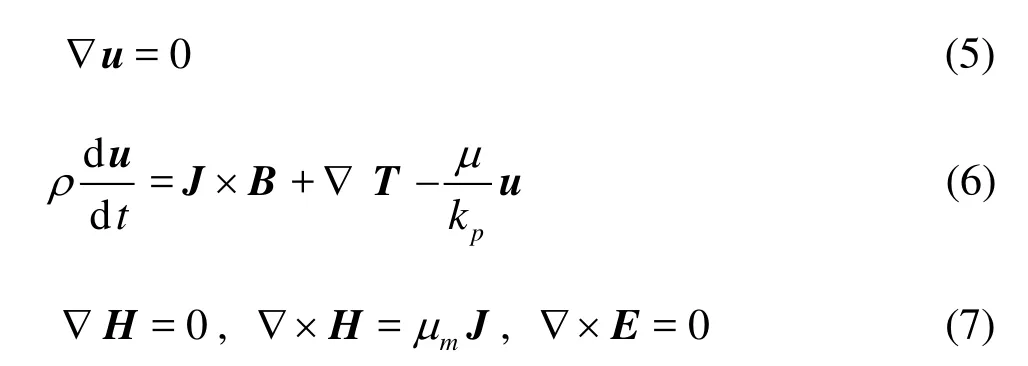
in which ρrepresents the fluid density,J, the current density,Hthe total magnetic field,μm, the magnetic permeability,E, the total electric field and kp, the permeability of the porous channel.

Considering the flow to be symmetric, we can confine the analysis of the model to the region0≤y≤h, for Ex[0,L], whereL represents the length of the channel (cf. Fig.1) The effect of gravity and the Joule heating effect, being quite small for the situation taken up for the present study, will be disregarded. The Debye lengthλis assumed to be much smaller than the channel height2h . Further, h is supposed to be much smaller than the widthw and the lengthL of the channel.

Fig.1 Physical sketch of the problem

Inserting Eq.(2) into Eq.(6) and making use of Eqs.(3), (4) and (7) and assuming Boussinesq incomepressible fluid model yield the boundary-layer equations[15,16]governing the second grade viscoelastic fluid in the presence of a time-periodic electric field

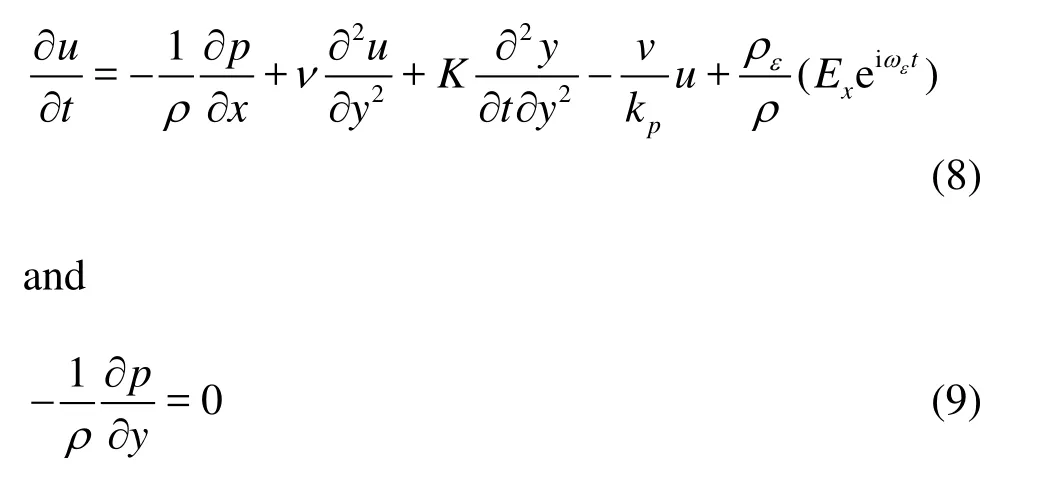
The charge density and electric potential are related to each other according to Gauss’s law of charge distribution. The relation is given by the equation

where ρe=2 n0ez sinh(e z/ KBTψ)represents the distribution of net electric charge density in equilibrium near a charged surface, as in a fully developed flow, weis the angular velocity of the AC electric field,Exis the amplitude of the field andt denotes the time. The electrical double layers are considered to be so thin that there is no mutual interference between the walls. The symbolsv,K,ρand kpdenote respectively the kinematic viscosity, viscoelastic coefficient, density and porous medium permeability coefficient.

Let us now introduce the following set of non-dimensional variables:

In Eqs.(11) and (12),UHSdenotes the Helmholtz-Smoluchowski electro-osmotic velocity, which is defined by

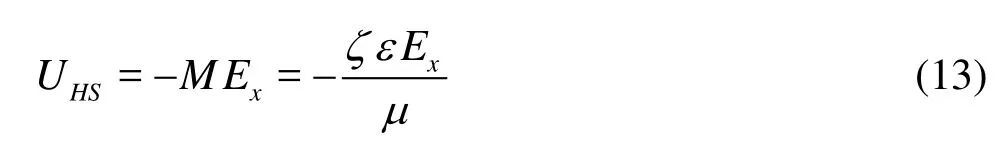
in which M stands for the mobility,ζfor the zeta potential,εfor the dielectric constant of the medium and u =ρvis the dynamic viscosity.

In terms of the dimensionless variables defined in Eqs.(11) and (12), Eqs.(8)-(10) can be rewritten in the form

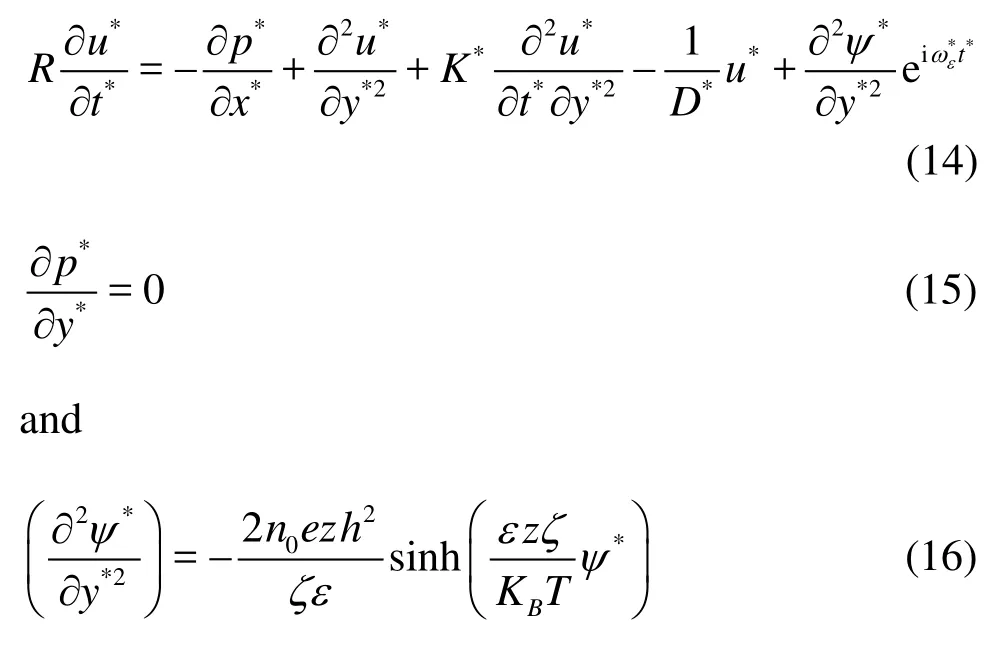
where m2is called the Debye-Huckel parameter (in the non-dimensional form) and is defined by

λbeing the thickness of the Debye layer.

The solution of Eq.(16) subject to the boundary conditions

In the sequel, we shall drop the superscript “∗” to give a more convenient look to the equations involving non-dimensional variables. To solve the Eqs.(14), (15) and (16), we further write the velocityuas u= useiw1t, whereusrepresents the steady part of the velocity (independent of time).

Now the boundary conditions applicable to our flow problem are,

Making use of these boundary conditions and the Eq.(14), we have derived the following equation

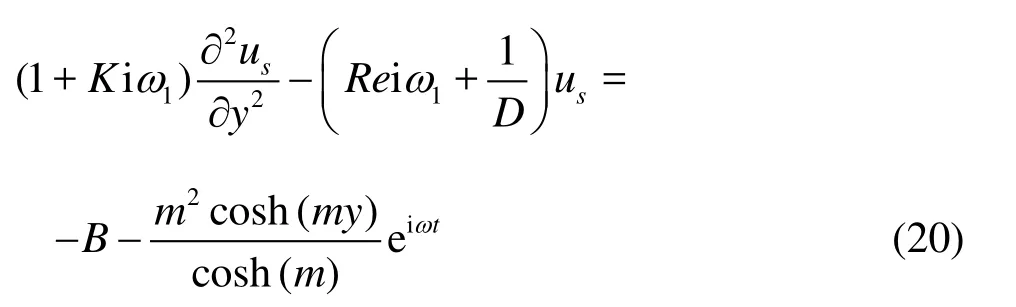
where w =we-ω1represents the difference between the angular velocity of the applied electric field and that of the oscillatory motion of the plates.

来自各级硫冷凝器的液硫随重力自流至液硫池(S-301)，在液硫池中通过Black&Veatch的专利技术MAG○R脱气工艺可将液硫中的硫化氢质量分数脱除至15×10-6以下[2]。MAG○R液硫脱气工艺无需采用任何化学添加剂，其工艺原理为:液硫在液硫池的不同分区中循环流动，并通过一、二级喷射器(EJ-302/303)进行机械搅动，溶解在液硫中的硫化氢释放到气相中并由蒸汽抽空器(EJ-301A/B)送入尾气焚烧炉焚烧[3]。

Solving the Eq.(20) subject to the boundary condition (19), we obtain,

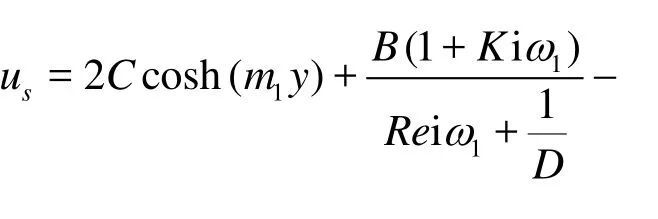
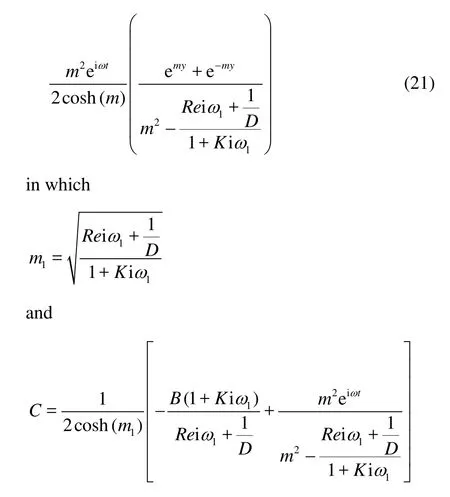
Equation (21) gives the required solution for the steady part of the electro-osmotic flow velocity, while for the problem under consideration at any instant, the fluid velocity is given by u= useiω1t. The numerical estimates of the velocity variations have been computed and presented graphically in the section that follows. They are quite useful to derive a variety of information in respect of different bio-medical applications.

2. Application: Quantitative estimates for physiological flows

In this section we want to present some numerical estimates that are useful to examine the variation in velocity distribution as well as the change in velocity as time progresses for different values of the parameters involved in the analysis of the problem. The software MATHEMATICA has been used for the purpose of computational work. In order to illustrate the applicability of the mathematical analysis presented in Section 1, we consider an example concerning the physiological problem of the hemodynamical channel flow of blood under the action of an applied alternating electric field. We have confined our computational work to electro-osmotic flows of blood in the microcirculatory system. With this end in view, the effects of the blood viscoelasticity parameter K, the Reynolds numberRe , the porous medium shape factor parameterD , the Debye-Huckel parameterm on velocity distribution of blood flow has been investigated thoroughly. For the purpose of computation of the concerned analytical expressions, we have made use of experimental data for different parameters for blood and its flow, as available from Refs.[17]-[20].

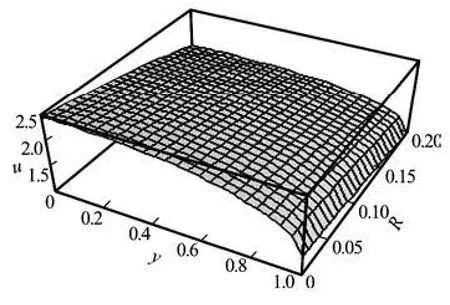
Fig.2 Distribution of blood velocity during electro-osmotic flow, in lower range values of Reynolds number Re, when m =50,t =5,D =0.1,B =30,K =0.005, we=50,ω1=20

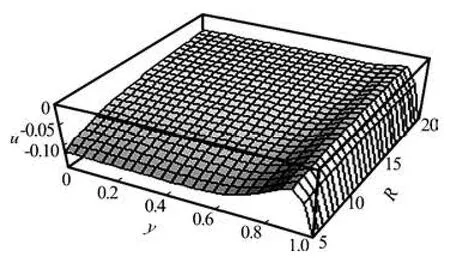
Fig.3 Distribution of blood velocity during electro-osmotic flow, in higher range values of Reynolds number Re, when m =50,t =5,D =0.1,B =30,K =0.005, we=50,ω1=20

Figure 2 provides an idea of the velocity distribution in the lower range of the Reynolds number Re. This figure reveals that with an increase in the Reynolds numberRe, the velocity of blood in a micro-channel decreases. But from Fig.3, it is revealed that the velocity increases with the increase in the Reynolds number (at a higher range values ofRe). Physically, the Reynolds number can be defined as a ratio between the inertia force and the viscous force. So, logically any increase in the Reynolds number causes a rise in the magnitude of the inertia force, and so the velocity should increase. But, for an electroosmotically actuated flow at lower values ofRe, flow due to electro-osmosis dominates first and with an increase in the value ofRe, the flow gradually turns out to be controlled by the inertia force arising out of the increasing value of Reynolds number. It is also to be observed from Fig.3 that the electrokinetic force is more dominant near the vicinity of the wall due to the formation of electrical double layer.

From Fig.4 it is observed that the velocity increases with a rise in porous medium shape factorD. The shape factor of porous medium is the ratio between the permeability coefficient and the square of the height of the channel. So, any increase in theporous medium permeability coefficient causes a rise in the velocity of the fluid (blood). Figure 5 illustrates that the amplitude of oscillation of blood velocity u increases as the value of the shape factorD is enhanced.

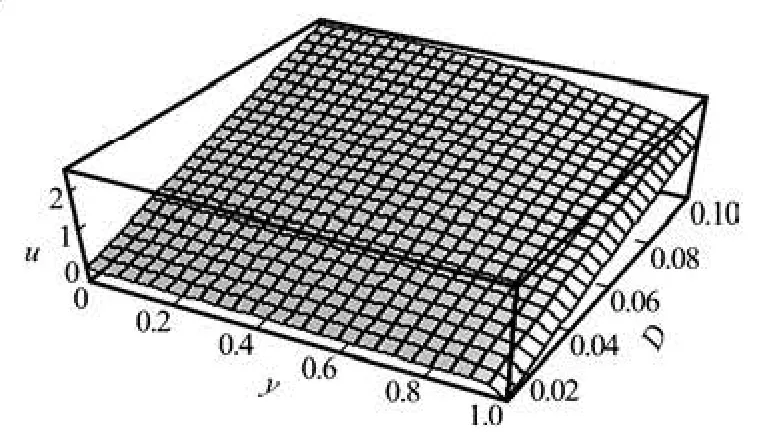
Fig.4 Variation in distribution of blood velocity during electroosmotic flow, for different values of porous medium shape factor parameter D, when m =50,t =5,Re= 0.001,B =30,K =0.005,we=50,ω1=20

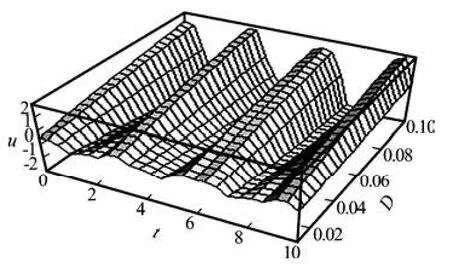
Fig.5 Variation in velocity field during electro-osmotic flow of blood with change in porous medium shape factor parameter D, when m =50,y =0.95,Re =0.01,B =30, K =0.005,we=5,ω1=2

Fig.6 Variation in velocity distribution in electro-osmotic blood flow with change in blood viscoelasticity (K), when m =50,t =5,D =0.1,B =30,Re =0.01,we=50, ω1=20

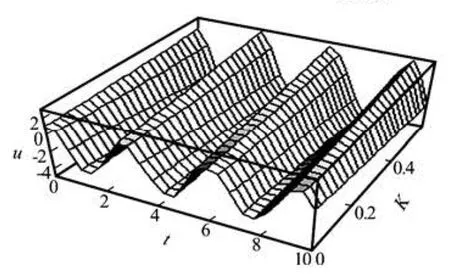
Fig.7 Change in velocity field of blood during electro-osmotic flow, with change in blood viscoelasticity (K), when m =50,y =0.9,D =0.1,B =30,Re =0.01,we= 5,ω1=2

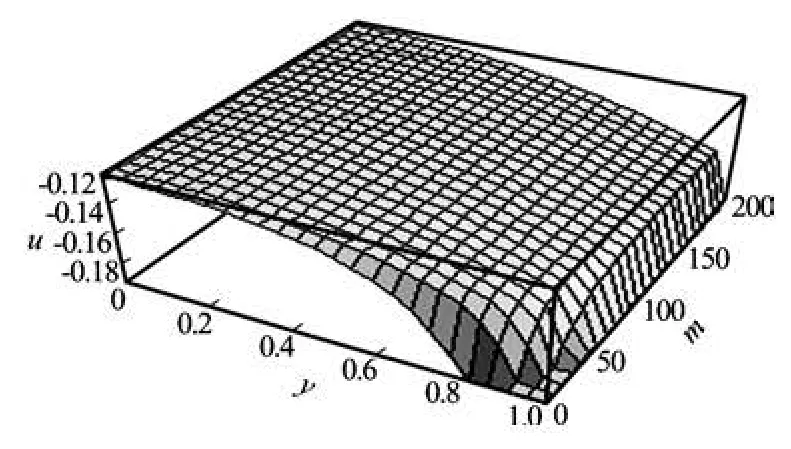
Fig.8 Change in distribution of electro-osmotic flow velocity of blood, as the value of the Debye-Huckel parameter m changes, where Re =0.1,t =10,D =0.1,B =30, K =0.005,we=500,ω1=200

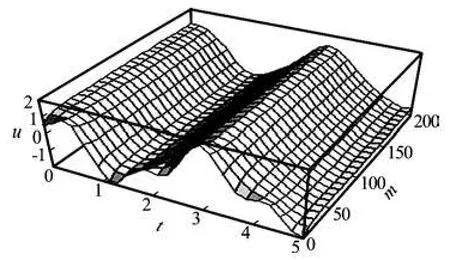
Fig.9 Change in distribution of electro-osmotic flow velocity with time as the value of the Debye-Huckel parameter m changes, when Re =0.1,y =0.9,D =0.1,B= 30,K =0.005,we=50,ω1=20

3. Concluding remark

The study has been motivated by recent developments of bio-sensing and high thought-put screening technologies for several important applications, such as sample collection for detection of viruses like adenovirus and Dengue Hemorrhagic fever. Basically the problem is formulated as a boundary-value problem concerning the flow of a second-grade viscoelastic fluid under the influence of electro-kinetic forces. The object of this theoretical investigation has been to have an idea of the distribution of the fluid velocity through a porous channel, with the change in different parameters of interest in the viscoelastic fluid flow pattern. The study serves as a first step towards a better understanding of the role of electro-osmosis in the viscoelastic flow pattern, which is oscillatory in nature, when influenced by an alternating electric field. The numerical estimates presented in the preceding section bear the potential of throwing some light on the electro-osmotic flow behavior of blood in the micro-circulatory system, when the system is under the influence of an external electric field. These results are expected to be of immense interest to clinicians and bio-engineers.

Acknowledgement

The authors wish to express their deep sense of gratitude to the esteemed reviewers for their comments on original version of the manuscript, based on which the revised manuscript has been prepared.

[1] STONE H. A., STROOCK A. D. and AJDARI A. Engineering flows in small devides: Microfluidics toward a lab-on-a-chip[J]. Annual Review and Fluid Mechanics, 2004, 36: 381-411.

[3] HLUSHKOU D., KANDHAI D. and TALLAREK U. Coupled lattice-Boltzmann and finite-difference simulation of velectroosmosis in microfluidic channels[J]. International Journal of Numerical Methods Fluids, 2004, 46(5): 507-532.

[4] HERR A. E., MOLHO J. I. and SANTIAGO J. G. et al. Electro-osmotic capillary flow with non-uniform zeta potential[J]. Analytical Chemistry, 2000, 72: 1053-1057.

[5] CHEN C.-I., CHEN C.-K. and LIN H.-J. Analysis of unsteady flow through a microtube with wall slip and given inlet volume flow variations[J]. Journal of Applied Mechanics, 2008, 75(1): 014506.

[6] YANG R. J., FU L. M. and LIN Y. C. Electro-osmotic flow in microchannels[J]. Journal of Colloid Interface Science, 2001, 239: 98-105.

[7] PIKAL M. J. The role of electroosmotic flow in transdermal ionotophoresis[J]. Advance Drug Delivery Reviews, 2001, 46(1-3): 281-305.

[8] TANG G. H., LI X. F. and HE Y. L. et al. Electroosmotic flow of non-Newtonian fluid in microchannels[J]. Journal of Non-Newtonian Fluid Mechanics, 2009, 157(1-2): 133-137.

[9] ZHAO C., ZHOLKOVSKIJ E. and JACOB H. et al. Analysis of electroosmotic flow of power-law fluids in a slit microchannel[J]. Journal of Colloid Interface Science, 2008, 326(2): 503-510.

[10] MISRA J. C., SINHA A. and SHIT G. C. Flow of a biomagnetic viscoelastic fluid: Application to estimation of blood flow in arteries during electromagnetic hyperthermia, a therapautic procedure for cancer treatment[J]. Applied Mathematics Mechanics, 2010, 31(11): 1405-1420.

[11] AKGUL M. B., PAKDEMIRLI M. Analytical and numerical solutions of electro-osmotically driven flow of a third-grade fluid between micro-parallel plates[J]. International Journal of Non-Linear Mechanics, 2008, 43(9): 985-992.

[12] DHINAKARAN S., AFONSO A. M. and ALVES M. A. et al. Steady viscoelastic fluid flow between parallel plates under electro-osmotic forces: Phan-Thien-Tanner model[J]. Journal of Colloid Interface Science, 2010, 344(2): 513-520.

[13] MISRA J. C., SHIT G. C. and CHANDRA S. et al. Electro-osmotic flow of a vis-coelastic fluid in a channel: Applications to physiological fluid mechanics[J]. Applied Mathematics and Computation, 2011, 217: 7932-7939.

[14] RIVLIN R. S., ERICKSEN J. L. Stress deformation relations for isotropic materials[J]. Journal of Rational Mechanics Analysis, 1955, 4: 323-425.

[15] MAKINDE O. D., MHONE P. Y. Heat transfer to MHD oscillatory flow in a channel filled with porous medium[J]. Rom Journal of Physics, 2005, 50(9-10): 931-938.

[16] HAMZA M. M., ISAH B. Y. and USMAN H. Unsteady heat transfer to MHD oscillatory flow through a porous medium under slip condition[J]. International Journal of Computer Applications, 2011, 33(4): 12-17.

[17] MISRA J. C., SHIT G. C. and RATH H. J. Flow and heat transfer of a MHD viscoelastic fluid in a channel with stretching wall: Some applications to hemodynamics[J]. Computers and Fluids, 2008, 37(1): 1-11.

[18] MISRA J. C., SHIT G. C. and CHANDRA S. et al. Hydromagnetic flow and heat transfer of a second-grade viscoelastic fluid in a channel with oscillatory stretching walls: Application to the dynamics of blood flow[J]. Journal of Engineering Mathematics, 2011, 69(1): 91-100.

[19] PAPADOPOULOS P. K., TZIRTZILAKIS E. E. Biomagnetic flow in a curved square duct under the influence of an applied magnetic field[J]. Physics of Fluids, 2004, 16(8): 29-52.

[20] TZIRTZILAKIS E. E. A mathematical model for blood flow in magnetic field[J]. Physics of Fluids, 2005, 17(7): 07710.

Nomenclature

(x, y)– Space coordinates in Cartesian system

u– Velocity of the fluid along x-direction

us– The steady value of the velocity

L– Length of the channel

Ex– Amplitude of the instantaneous electric field applied externally

E– Value of dc electric field

v – The kinematic viscosity

K– The coefficient of viscoelasticity

kp– Porous medium permeability coefficient

e– Charge of an electron

z – Absolute value of the ionic valance

KB– Boltzmann constant

T– Temperature in Kelvin scale

no– Ionic number concentration

ω– The angular velocity

ψ– Potential field in the transverse direction (induced)

ζ– Wall zeta potential

ε– Dielectric constant

ρ– Density of the fluid

ρe– Electric charge density

v – The kinematic viscosity

m– Non-dimensional Debye-Huckel parameter

µ– Dynamicor viscometric viscosity

p– Pressure

D =k/h2– Porous medium shape factor parameter

p

λ– The thickness of electrical double layer

B– Amplitude of the instantaneous pressure

ωe– Angular velocity of the applied electric field ω1– Angular velocity of the oscillatory plates

M– Mobility

h– Half-width of the channel

Re – Reynolds number

10.1016/S1001-6058(13)60368-6

* Biography: MISRA J. C. (1944-), Male, Ph. D., Professor