An experimental study on runup of two solitary waves on plane beaches*
XUAN Rui-tao (宣瑞韬), WU Wei (吴卫)
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: wwsjt@online.sh.cn
LIU Hua (刘桦)
School of Naval Architecture, Ocean and Civil Engineering and MOE Key Laboratory of Hydrodynamics, Shanghai Jiao Tong University, Shanghai 200240, China
An experimental study on runup of two solitary waves on plane beaches*
XUAN Rui-tao (宣瑞韬), WU Wei (吴卫)
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: wwsjt@online.sh.cn
LIU Hua (刘桦)
School of Naval Architecture, Ocean and Civil Engineering and MOE Key Laboratory of Hydrodynamics, Shanghai Jiao Tong University, Shanghai 200240, China
(Received March 22, 2013, Revised March 28, 2013)
Experiments of the runup of two solitary waves on a plane beach are carried out in a wave flume. The two solitary waves with the same amplitude and the crest separating distances are generated by using an improved wave generation method. It is found that, with regard to the two solitary waves with same wave amplitude, the runup amplification of the second wave is less than that of the first wave if the relative crest separating distance is reduced to a certain threshold value. The rundown of the first solitary wave depresses the maximum runup of the second wave. If the leading solitary wave is of relatively smaller amplitude for the two solitary waves, the runup amplification is affected by the overtaking process of two solitary waves. It turns out that the runup amplification of the second wave is larger than that of the first wave if the similarity factor is approximately larger than 15, which means the larger wave overtakes the smaller one before the waves runup on a beach.
solitary wave, runup, beach, multiple solitary waves, experiment
It has been a traditional subject to understand the runup of long wave propagating over a constant depth region and then climbing up a sloping beach of constant slope because of importance of predicting tsunami runup on beaches[1]The runup of solitary wave measured by Synolakisare compared well with his analytical solution for n[2]nbreaking waves on a plane beach. Li and Raichlenproposed a nonlinear solution to the classical shallow water equation by using a hodograph transformation and reported an experimental study on runup process of nonbreakin[3]and breaking solitary wave. Fuhrman and Madsenproposed the reduced surf similarity parameter for solitary waves, the beach slope divided by the offshore wave height to depth ratio, which provides good coherency with experimental breaking and runup data and analytical no[n4b]reaking runup expressions. Recently, Chan and Liuext[5]nded the analytical approach of Madsen and Schäfferto study the runup formulae of a train of solitary waves and concluded that, for the runup of two solitary waves where a wave is followed by one with a larger amplitude, the maximum runup is slightly smaller than that of a single solitary wave. However, there are few works on experimental study on runup of a wave train of multiple soliton–like waves against a vertical wall or a plane beach.
We carried out experiments on the runup characteristics of two solitary waves in the wave flume of the MOE Key Laboratory of Hydrodynamics in Shanghai Jiao Tong University. The facility consists of a wave flume (65 m long×1.8 m deep×0.8 m wide), a piston-type wave generation system and a wave elevation measurement system. As shown in Fig.1, left side of the wave flume equipped with the piston-type wave generator is installed at one end of the wave flume and the paddle is moved horizontally in a prescribed trajectory by means of a hydraulic servosystem. At another end of the wave flume, a slope beach is installed to eliminate the wave reflection. There are total 12 wave gauges along the wave flume,which includes 11 gauges in the constant depth region and the remaining one at the slope to record the moving shoreline. The maximum wave runup is recorded by two high-speed cameras with 100 Hz record frequency and 1 024×1 024 resolution.
The improved Goring[6]wave generation methodology proposed by Malek-mohammadi and Testik[7], which takes the non-steady-state characteristics of the piston-type wave generator during the wave generation process into account, is used to implement wave generation in a wave flume. Based on the permanent waveform hypothesis, the velocity of water particle in front of the wave paddle is equal to that of the wave paddle, so the velocity of wave paddle can be expressed as

wheret is the time,u(ξ,t)is the depth-averaged horizontal velocity,d is the still water depth andη is the free surface elevation above the still water level.
Using the fourth-order Runge-Kutta method to solve the ordinary differential equation under specified wave profile, we can obtain the wave paddle trajectory ξ. For the two solitary waves, wave paddle stroke S =2(H1k1d+ H2k2d )and its duration T= 3.8(1/k1c1+1/k2c2)S /2(1/c1+1/c2). Here k1and k2are the wave number,c1and c2are the celerity of two successive solitary waves. The initial position of the wavemaker paddle is

The third-order solitary wave solution η(x1, t) are used as the target wave profile in order to improve the accuracy of solitary wave with large amplitude. Assuming the initial positions of two solitary wave crests are located at x=X1and x=X2. The wave profile of the two solitary waves at t=0can be expressed as a linear superposition formulation

where α1=H1/dand α2=H2/dare relative wave heights, sh stands for sech[k1( x -X1)]and th stands fortanh[k1( x -X1)], SH stands for sech[k2(x-X1)+ εσ]and TH stands for tanh[k2(x -X1)+ εσ], k1and k2are wave numbers,εσis the phase shift between these two solitary waves, which reflects the separating distance between crests of two solitary waves. Here,σis defined as σ=k( cT -S),Tis the duration of plane motion,Sis the stroke of plane motion, which adopted the parameters of the posterior solitary wave. Besides,εrepresents the initial phase, we adopted fiveεvalues of incident two solitary waves here, including 0.2, 0.4, 0.6 0.8 and 1.0.
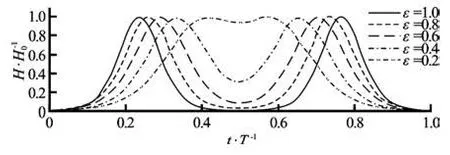
Fig.1 Two solitary waves with same amplitude
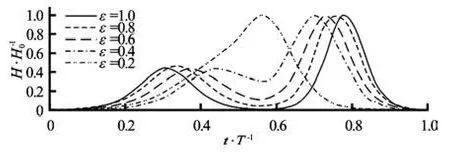
Fig.2 Two solitary waves with different amplitude
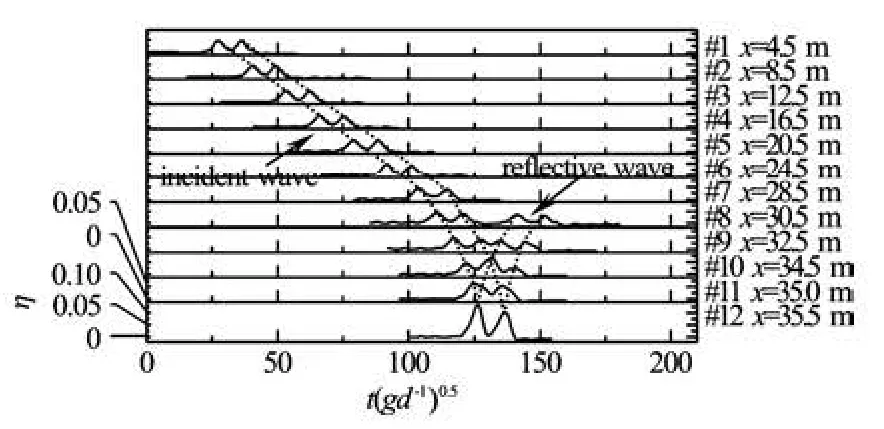
Fig.3 Time series of surface evolution and waterline on 45oslope for the two solitary wave with same amplitude (β=45o,H1/d =0.167,H2/d =0.167,ε=0.4)


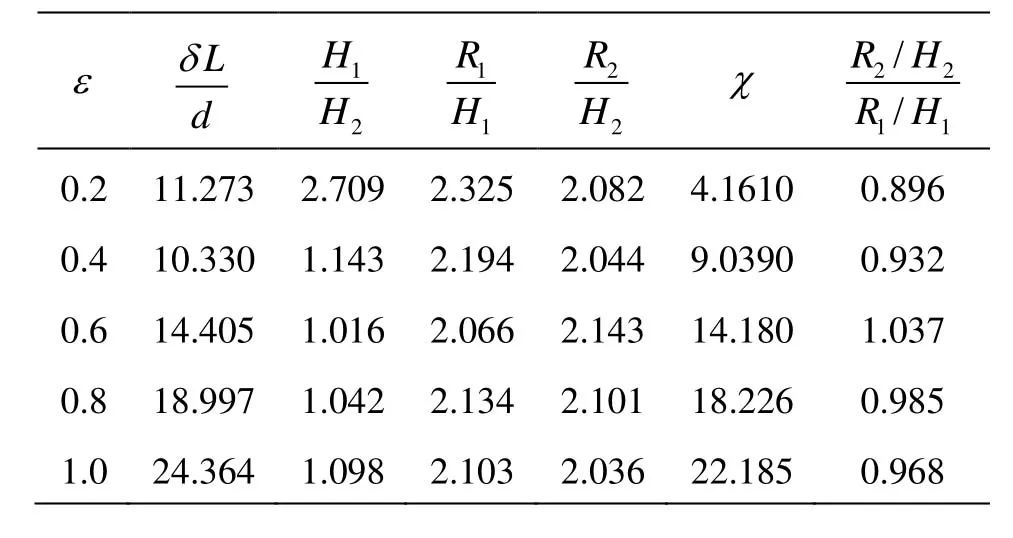
Table 1 Comparison of runup amplification on 45oslope for two solitary waves with same amplitude
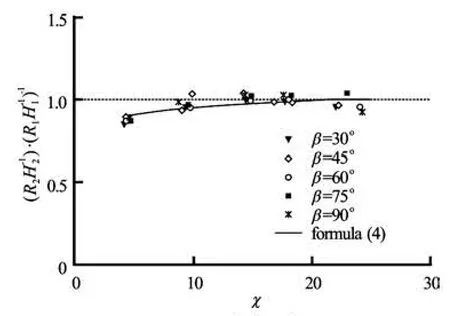
Fig.4 Relationship of runup amplification and the similarity factor of two solitary waves with same wave amplitude
The factor χis defined as (δ L/ d )/(H1/H2) which stands for a similarity factor of the two solitary waves.δL,H1and H2are measured at the location, which is close to the toe of slope but not be affected by the reflected waves. The runup amplification and the similarity factor can be found in Table 1.(R2H2)/ (R1H1)is ratio of the runup amplification of two waves, indicating the impact of the runup of the leading wave on the runup of successive waves. The runup amplification of the second wave is basically smaller than that of the second wave. The relationship of the new similarity parameter (R2H2)/(R1H1)andχ is presented in Fig.4. The empiric formula of the runup amplification in terms of the factorχis proposed as following (R2H2)/(R1H1)is approaching to 1.0 asχis larger than a threshold value, i.e., the runup associated with the second wave is no long affected by the rundown flow of the first wave. However,(R2H2)/(R1H1)is decreasing with the decrease ofχdue to the effects of rundown flow of the first wave.

If we look at the interaction of two solitary waves propagating at the same direction along a wave flume, it is expected that, for the case of a solitary wave with smaller amplitude followed by one of larger amplitude at the initial time, the solitary wave with larger amplitude will overtake the solitary wave with smaller amplitude. This is called the overtaking collision of two solitary waves. If the first wave is of larger amplitude at the initial time, these two solitary waves will separate each other because the solitary wave with large amplitude propagates at higher speed.
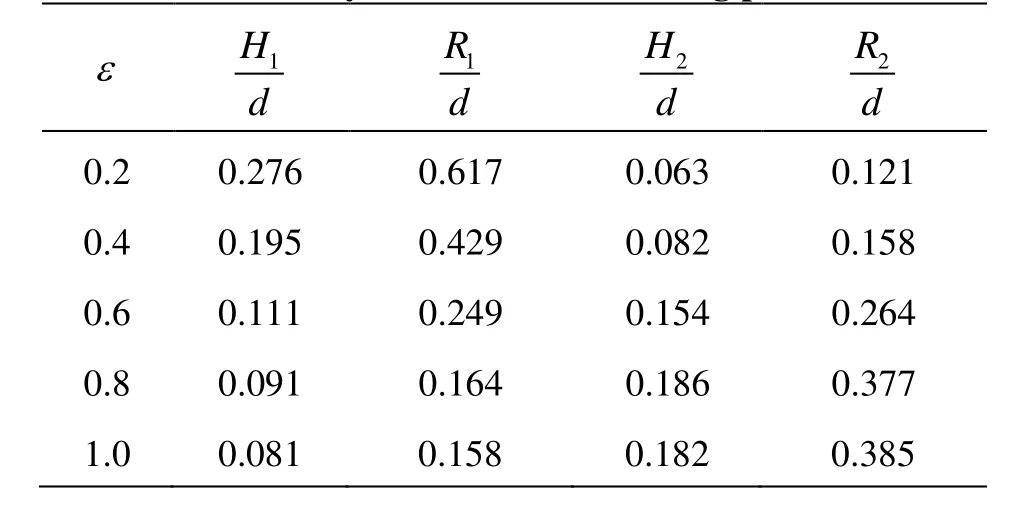
Table 2 Comparison of maximum runup on 45oslope for two solitary waves with overtaking process
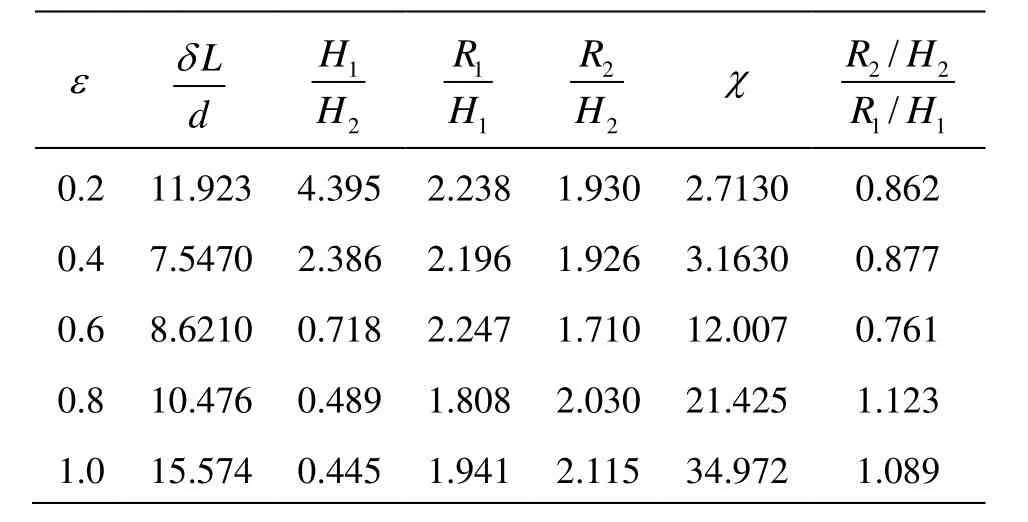
Table 3 Comparison of runup amplification coefficient on 45oslope for two solitary waves with overtaking process
The experimental investigation on the runup of the two solitary waves with different amplitude is concentrated on the effects of nonlinearity and transient property on the runup amplification. The initial relative wave amplitude and the crest separating distance of the two waves and the measured maximum runup of the two solitary waves on a plane beach of 45oslope are shown in Table 2. The corresponding runup amplification is shown in Table 3. It can be found thatthe runup amplification R2/ H2is larger than R1/ H1for the cases of the smaller wave runup on the slope firstly asεis equal to 0.8 and 1.0, while R2/ H2is smaller than R1/ H1for the case of ε=0.6. It is found that the larger wave will overtake the smaller one at the beach toe ifεis less than 0.6.
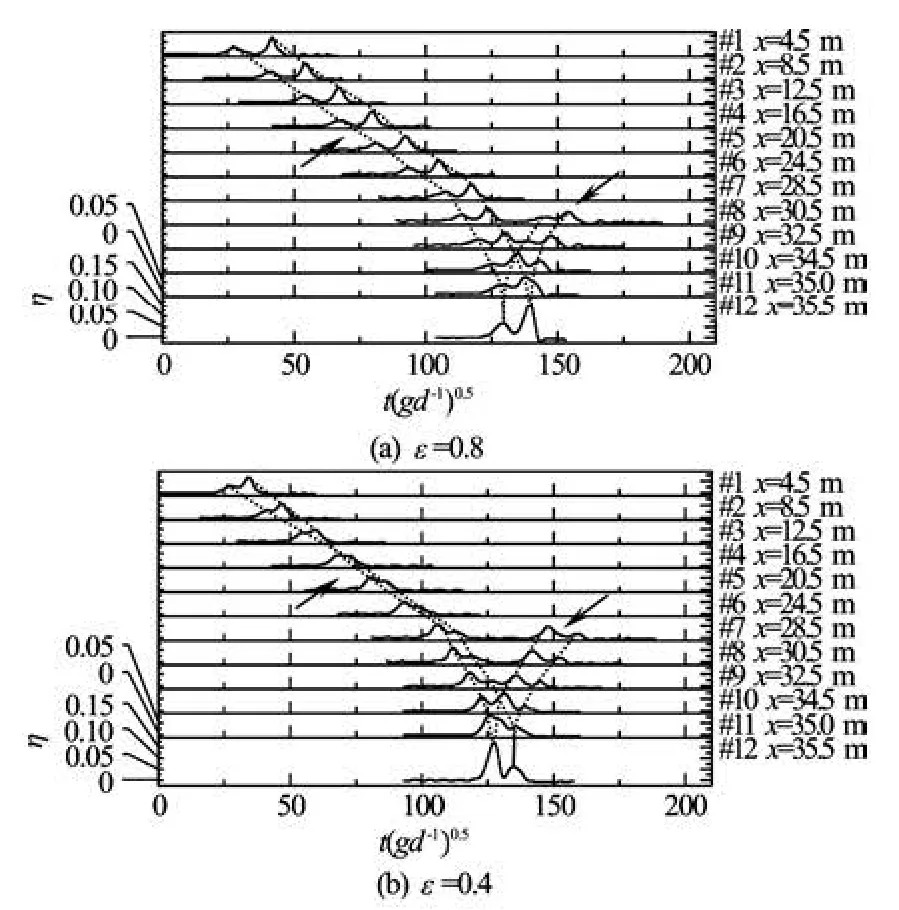
Fig.5 Time series of surface evolution and waterline on 45oslope for the two solitary wave with different wave amplitude (β=45o,H1/d =0.1,H2/d =0.233)
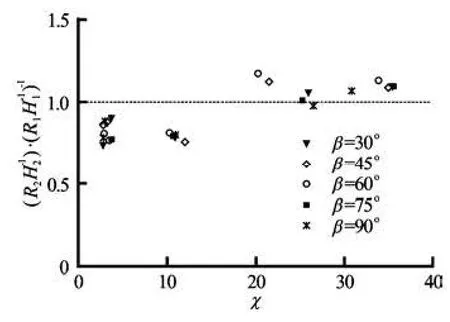
Fig.6 Relationship of runup amplification and the similarity factor of two solitary waves with different amplitude
Experimental results of the time series of the surface elevation measured by the wave gauges shows that the second wave is overtaking the first wave because the celerity of larger wave is faster than that of smaller wave, as shown in Fig.5. For the case ofε being equal to 0.2 and 0.4, the first runup measured by the wave gauge is generated by the larger wave initially following the smaller one. Actually, this kind of the two solitary waves belongs to transient waves, even though it holds some kind property of the solitary wave ties due to the balance of nonlinearity and dispersion of waves.
As shown in Fig.6, it turns out that, when factor χis approximately less than 15, the successive larger solitary wave overtakes the first smaller wave leads to the ratio of the runup amplification (R2H2)/(R1H1)is less than 1.0. If the factorχis large enough, which means the smaller solitary wave runup on the slope firstly, the ratio of runup amplification(R2H2)/(R1H1)is slightly larger than 1.0. It should be noted that the complicated flows and the surface oscillation in the stage of the rundown process of the first wave affects the runup of the second wave on a plane beach.
In summary, for the runup of two solitary waves where two wave have the same amplitude, the runup of the second wave is weaken by the first wave which results in the runup amplification coefficient is less than 1.0 as the distance between two wave crests is small. If two wave separate far enough, there is no interaction of two solitary waves for the runup process on beaches. The runup flows of the first solitary wave weaken the maximum runup height of the second wave. For the case of two solitary waves where a wave is followed by one with larger amplitude, when the factorχis less than 15, i.e., the wave with larger amplitude overtakes the leading wave before runup on the slope, and the runup amplification is less than 1.0 for the cases of smaller values of the similarity factor. If the similarity factor χis larger than a threshold value, which means the smaller wave runup on the slope firstly, the runup amplification of the second wave is larger than that of the first wave.
[1] SYNOLAKIS C. E. The run-up of solitary waves[J]. Journal of Fluid Mechanics, 1987, 185: 523-545.
[2] LI Y., RAICHLEN F. Solitary wave runup on plane slopes[J]. Journal of Waterway Port Coastal Ocean Engineering, 2001, 127(1): 33-44.
[3] FUHRMAN D. R., MADSEN P. A. Surf similarity and solitary wave runup[J]. Journal of Waterway Port Coastal Ocean Engineering, 2008, 134(3): 195-198.
[4] CHAN I. C., LIU P. L.-F. On the runup of long waves on a plane beach[J]. Journal of Geophysical Research, 2012, 117(C8): C08006.
[5] MADSEN P. A., SCHÄFFER H. A. Analytical solutions for tsunami runup on a plane beach: Single waves, N-waves and transient waves[J]. Journal of Fluid Mechanics, 2010, 645: 27-57.
[6] GORING D. G. Tsunamis-the propagation of long waves onto a shelf[D]. Doctoral Thesis, Pasadena, CA, USA: California Institute of Technology, 1978.
[7] MALEK-MOHAMMADI S., TERSTIK Y. F. New methodology for laboratory generation of solitary waves[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 2010, 136(5): 286-294.
10.1016/S1001-6058(13)60369-8
* Project supported by the National Natural Science Foundation of China (Grant No. 10972138), the Natural Science Foundation of Shanghai Municipality (Grant No. 11ZR1418200).
Biography: XUAN Rui-tao (1987-), Male, Master
LIU Hua, E-mail: hliu@sjtu.edu.cn
- 水动力学研究与进展 B辑的其它文章
- Electro-osmotic flow of a second-grade fluid in a porous microchannel subject to an AC electric field*
- Parametric instability of a liquid metal sessile drop under the action of low-frequency alternating magnetic fields*
- Influence of flow field on stability of throttled surge tanks with standpipe*
- Influence of emergent macrophyte (Phragmites australis) density on water turbulence and erosion of organic-rich sediment*
- Hydrodynamic performance of a vertical-axis tidal-current turbine with different preset angles of attack*
- Observation of the induced pressure in a hybrid micro/nano-channel*

