MK-LSSVM与AdaBoost-SVM在分类中的比较和研究
刘卫华
(兰州交通大学自动化与电气工程学院,甘肃 兰州 730070)
0 引言
支持向量机(support vector machine,SVM)作为一种新的数据分类和函数估计方法[1],越来越受到人们的重视。近几年出现了许多对标准支持向量机的改进方法,最小二乘支持向量机(least squares support vector machines,LS-SVM)[2]就是其中的一种。该方法采用等式约束代替了标准支持向量机的不等式约束,其实质是求解线性方程组,这极大地简化了计算的复杂性,提高了训练速度和测试速度。
集成分类方法是将多个弱分类器通过一定的策略组装,充分利用多个弱分类器的特性,达到提高总的分类精度的目的。AdaBoost是集成分类方法中具有代表性的算法,将支持向量机(SVM)作为弱分类器的一种新的集成分类算法[3](AdaBoost-SVM)已经得到了广泛应用。
本文分别将改进的多核LS-SVM算法和AdaBoost-SVM算法应用于心脏单光子发射计算机化断层显像(single photon emission computerized tomography,SPECT)图像数据和iris数据的分类问题,并且给出分类的可视化效果图。试验结果表明,改进的多核LS-SVM算法和AdaBoost-SVM算法都能取得较好的分类精度,且多核LS-SVM算法耗时较短。
1 最小二乘支持向量机
1.1 最小二乘支持向量机分类
LS-SVM算法的数学表达式如下:设训练样本集D= { (xi,yi)}(i=1,…,N,xi∈Rn,yi∈R),其中 xi表示输入数据,yi表示输出类别。LS-SVM的原始分类问题可以表述为:
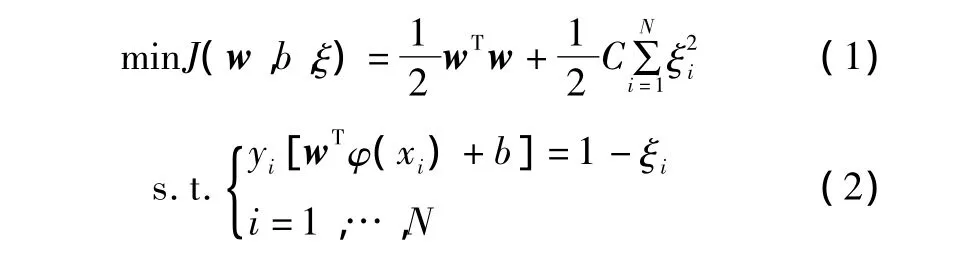
构造拉格朗日函数,可表示为:

式中:拉格朗日乘子αi∈R。
对式(3)进行优化,可表示为:
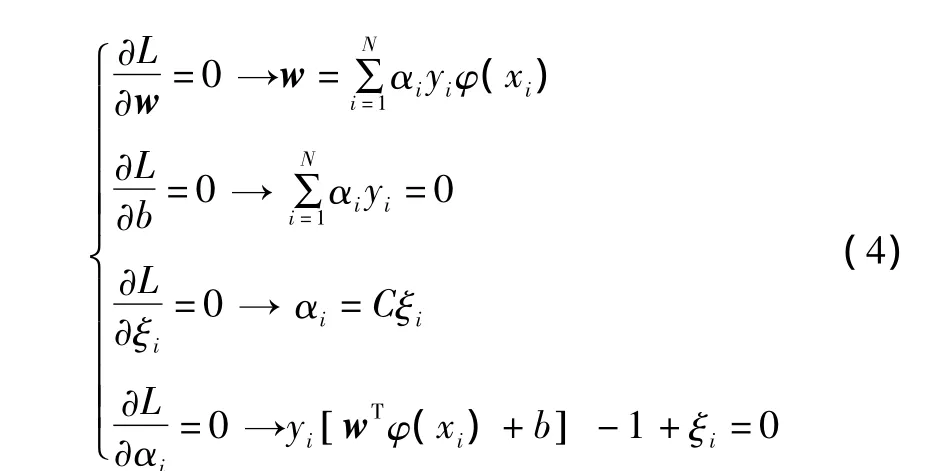
忽略w、ξ,由式(4)可以得到线性方程组,其表达式为:

将Mercer条件应用到矩阵Ω=ZZT中,得到:

因此,式(1)的原始分类问题通过求解式(5)的线性方程可以获得,于是可以得到决策函数为:

式中:sign为符号函数;b为分类阈值;αi为拉格朗日乘子。
1.2 多核最小二乘支持向量机
基于多核核函数[4-5]的最小二乘支持向量机(multiple kernel least squares support vector machine,MK-LSSVM)算法是将不同类型的核函数进行凸组合,得到新的等价核函数,其表达式为:

式中:λk为不同核函数的加权系数[6]。
由核函数的性质可知,等价核函数满足Mercer条件。
MK-LSSVM的原始问题变为:

2 AdaBoost-SVM算法
AdaBoost分类算法是以寻求高分类精度为目标的一种迭代的训练算法,它是将多个弱分类器经过一定的策略组合,最终求得一个强分类器的过程[7]。在这个过程中,主要是通过改变样本的权重系数来改变样本分布,对于错误分类的样本增大其相应的权重系数,同时降低正确分类样本的权重系数。经过T次迭代循环,得到了T个基分类器和T个与其对应的权重系数,最后把这T个基分类器按权重系数叠加,从而得到最终的强分类器[8]。
算法过程示意图如图1所示。
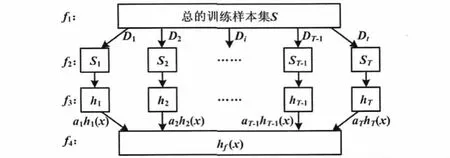
图1 算法过程示意图Fig.1 Schematic diagram of the algorithm process
目前,神经网络、决策树等方法已经被用来作为AdaBoost的弱分类器,但都存在弱分类器本身的参数以及训练次数T选取难的问题。将SVM作为弱分类器很好地解决了以上问题[9]。当SVM采用径向基核函数时,它的分类性能只受高斯宽度σ和惩罚因子C的影响。只要给定一个适当的C值,SVM的性能就会很大程度上依赖σ的取值。
AdaBoost-SVM算法的训练步骤[10]如下。
① 给定含有标签的训练样本集S={(x1,y1),…,(xN,yN)},事先设定循环迭代次数为 T、误差ε*、线性SVM 参数 δ1={C1,C2,C3,…}与采用 RBF 核的非线性 SVM 参数 δ2={(C1,σ1),(C2,σ2),...},并且令δ = δ1∪δ2。
② 采用AdaBoost求出各个基分类器h1,h2,…,hT及其权重α1,α2,…,αT。假设 ψ(x)=[α1h1(x),α2h2(x),…,αThT(x)],则 训 练 集 S={[ψ (x1),y1],…,[ψ(xN),yN]}。
③ 由以下步骤获得SVM的参数δi∈δ。
对训练样本集S做训练,并利用交叉验证优化方法确定其误差 ε。若 ε < ε*,则设 ε*=ε、δ*=δi。
④设定SVM的参数为δ*,并输出训练后的强分类器。
3 试验及结果分析
本试验在一台2.13 GHz、内存2 GB的DELL个人计算机上运行,在Matlab R2007b环境下实现。
将LS-SVM算法和AdaBoost-SVM算法分别应用于二分类问题和多分类问题,所用的数据样本有心脏单光子发射计算机化断层显像(SPECT)图像数据、Iris数据集。由于数据都是具有多个属性的高维数据集,文中采用Sammon算法将高维输入空间的数据映射到二维输出空间中予以显示,从而使分类结果可视化。
①SPECT图像数据试验
SPECT数据集包含两个数据集:SPECT Heart数据集和SPECTF Heart数据集,这些数据描述了心脏诊断的单质子发射计算机断层摄影图像。数据集共包含267个样本,SPECT Heart数据集共有 22个属性,SPECTF Heart数据集共有44个属性。
试验过程中,SPECT数据取80个样本为训练数据,剩下的作为测试数据;迭代次数T取3,惩罚参数C以及核参数由交叉验证优化方法寻优得到。采用LSSVM、AdaBoost-SVM和MK-LSSVM这3种方法得到的数据分类试验结果如表1所示。

表1 数据分类试验结果Tab.1 Classification test results of heart data
由表1可以看出,3种方法都能达到较好的分类效果。从分类精度来看,MK-LSSVM算法略优于普通LS-SVM算法和AdaBoost-SVM算法;从平均训练时间来看,由于在选型阶段多核比普通RBF核需要更多的搜索时间,所以MK-LSSVM算法的训练与测试耗时都比普通的LS-SVM算法稍长些,但与AdaBoost-SVM算法相比较,MK-LSSVM算法明显提高了训练速度。
②Iris数据试验
Iris鸢尾花数据集选自UCI机器学习数据库。该数据集包含150个样本,分为3类,每类含50个样本。样本共有4种属性:萼片宽度、萼片长度、花瓣宽度和花瓣长度。该数据集被认为是目前模式识别中最好的测试数据集。
Iris数据分别选取的训练样本数为40、60、80、100、120、140,随机抽取80个数据作为测试样本。采用LSSVM、AdaBoost-SVM和MK-LSSVM这3种算法分别对选取不同训练样本数目时的Iris数据集进行试验,迭代次数T取10,惩罚参数C以及核参数由交叉验证优化方法寻优得到。在样本数目大小不同的情况下,3种方法的分类性能如图2所示。

图2 3种算法分类性能曲线比较Fig.2 Classification performance curves of three kinds of algorithms
由图2可以看出,对多分类问题中的Iris数据集进行性能测试时,这3种算法的分类精度都相应地随着训练样本数目的增加而不断提高。当训练样本较少时,MK-LSSVM算法的分类精度高于其他两种算法,并且当训练样本数增加到一定数目时,MK-LSSVM算法的分类精度可以达到100%。
Iris数据经过MK-LSSVM分类器分类并通过Sammon映射后在二维平面的分类可视化图如图3所示。

图3 Iris数据集分类可视化图Fig.3 Visualized diagram of Iris data classification
4 结束语
本文比较研究了MK-LSSVM和AdaBoost-SVM这两种分类器方法。MK-LSSVM算法是最小二乘支持向量机的一种改进算法,它将多核学习的理念与最小二乘支持向量机相融合,降低了分类精度对核函数选择的依赖性。AdaBoost-SVM算法是通过选择合适参数,将支持向量机作为一种弱分类器,通过循环迭代而最终得到强分类器。
将MK-LSSVM和AdaBoost-SVM这两种方法应用于二分类问题和多分类问题中,通过试验数据结果可知,这两种方法都能获得较好的分类精度,但AdaBoost-SVM算法耗时较长;从经Sammon映射的分类可视化图可以看出,在Iris数据分类中,MK-LSSVM算法的分类精度可达到100%,而AdaBoost-SVM算法的平均耗时要比MK-LSSVM算法长。
[1]Cristianini N,Shawe-Taylor J.支持向量机导论[M].李国正,王猛,曾华军,译.北京:电子工业出版社,2004.
[2]Suykens J A K,Vandewalle J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[3]阎威武,邵惠鹤.支持向量机和最小二乘支持向量机的比较及应用研究[J].控制与决策,2003,18(3):358-360.
[4]Taylor J S,Cristianini N.Kernel methods for pattern analysis[D].Cambridge:Cambridge University,2004.
[5]汪洪桥,孙富春,蔡艳宁,等.多核学习方法[J].自动化学报,2010,36(8):1037-1050.
[6]陈强,任雪梅.基于多核最小二乘支持向量机的永磁同步电机混沌建模及其实时在线预测[J].物理学报,2010,54(4):2310-2318.
[7]朱树先,张仁杰,郑刚.混合核函数对支持向量机分类性能的改进[J].上海理工大学学报:自然科学版,2009,31(2):173-176.
[8]Li Xuchun,Wang Lei,Sung Eric.AdaBoost with SVM-based component classi fi ers[J].Engineering Applications of Arti fi cial Intelligence,2008(21):785-795.
[9]胡金海,谢寿生,杨帆,等.基于支持向量机的组合分类方法及应用[J].推进技术,2007,28(6):669-673.
[10]张晓龙,任芳.支持向量机与AdaBoost的结合算法研究[J].计算机应用研究,2009,26(1):77-78,110.

