基于非线性滤波算法的磁偶极子跟踪

吴志东, 周穗华, 陈志毅



基于非线性滤波算法的磁偶极子跟踪

吴志东, 周穗华, 陈志毅

(海军工程大学 兵器工程系, 湖北 武汉, 430033)

为了实现具有高度非线性特点的磁偶极子跟踪, 将磁偶极子的位置、速度和磁矩等参数的估计归结为动态系统的贝叶斯估计问题, 提出了使用递归方法估计其状态参数。在此基础上应用高斯混合采样粒子滤波(GMSPPF)算法实现了磁偶极子跟踪, 并通过实测试验检验了算法的性能。结果表明, 与粒子滤波(PF)和Sigma点粒子滤波(SPPF)算法相比, GMSPPF算法具有更好的性能和较低的计算量。

磁偶极子跟踪; 贝叶斯估计; 高斯混合采样粒子滤波算法

0 引言

磁性舰船目标跟踪具有隐蔽性好、磁场信号穿透性强等优点, 在自动观测系统中有重要价值。对磁性舰船目标进行远距离跟踪时, 经常使用磁偶极子模型来描述舰船的磁场特征[1-2]。

磁偶极子跟踪属于被动无源跟踪问题[3-6], 具有高度非线性的特点, 无法通过解析方法得到其最优解。文献[3]~[6]均采用了非线性滤波方法解决磁偶极子跟踪问题。其中, 文献[3]和[4]使用扩展卡尔曼滤波(extend Kalman filter, EKF)方法和2个三分量磁传感器实现了磁偶极子跟踪, 但EKF方法需要求解观测函数的雅克比矩阵计算量较大, 且只有1阶近似精度对高阶非线性问题的优化效果不理想[7-8]。文献[5]使用不敏卡尔曼滤波(unscented Kalman filter, UKF)方法解决磁偶极子跟踪问题, 但跟踪的精度不高, 相对于EKF方法, 性能提升有限。相比文献[5], 文献[6]使用不敏粒子滤波(unscented particle filter, UPF)方法实现了曲线运动情况下的磁偶极子跟踪, 跟踪精度较高。该算法提高了标准粒子滤波(particle filter, PF)算法的性能并可用于解决非线性、非高斯问题, 但计算量较大。Rudolph M在文献[9]中提出1种高斯混合采样粒子滤波(Gaussian-mix- ture sigma-point particle filter, GMSPPF)算法, 该算法提高了Sigma点粒子滤波(sigma-point particle filter, SPPF)算法的性能并大大降低了计算量, 可以用于解决磁偶极子跟踪问题。

论文讨论了如何通过测量磁偶极子的磁场特征来反演出偶极子的位置、速度和磁矩等参数的问题; 提出了使用高斯混合采样粒子滤波算法跟踪磁偶极子的方法, 将跟踪过程视为可以用状态图变换来描述的动态模型, 并且利用递归贝叶斯估计理论和目标状态向量服从1阶马尔科过程的假设。论文还用状态空间方法对跟踪问题的离散时间事件进行了建模, 以达到使用测量值估计出隐藏的状态参数的目的。同时使用磁通门传感器和磁偶极子目标进行实测实验, 以检验算法的性能。

1 磁偶极子跟踪的理论分析

1.1 算法原理

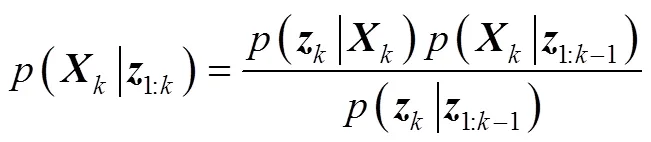
由于磁性偶极子观测方程的高度非线性和自身运动方向的不确定性, 使其不能服从线性、高斯分布。对于一般的非线性、非高斯系统, 上述滤波方法很难得到后验概率的封闭解析式。因此, 多使用非线性滤波方法以获取待估计问题的次优解。现有的非线性滤波方法主要有EKF、高斯滤波方法、UKF和PF等[11]。但前3种方法假设后验概率密度为高斯分布, 不适用于一些非线性、非高斯的情况。

基于序贯重要性采样的粒子滤波方法在解决非线性、非高斯问题上已得到成功应用。但是PF算法存在着粒子退化和贫化等缺陷, 为了解决此问题, 文献[9]提出了GMSPPF用以提高PF算法的性能并降低SPPF算法的计算量。该算法利用有限高斯混合模型表征后验概率分布情况, 可以通过基于重要性采样加权的后验粒子, 借助于加权的期望最大化算法替换标准重采样步骤, 解决了粒子贫化问题。算法实现的主要原理如下。

1.2 磁偶极子跟踪的状态和观测模型

对于磁偶极子跟踪问题而言, 该问题的状态变量由以下2部分组成: 描述目标运动状态的速度、位置参数; 描述目标磁性特征的磁矩参数。假设偶极子目标在水平面内匀速直线运动, 即目标的垂直位置为常数且速度为零, 则系统的状态向量是

式(3)对应于状态方程, 可以看出状态方程是线性函数, 式(8)对应于观测方程, 可以看出观测方程是高度非线性函数。

2 实测试验与结果分析

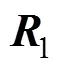
表1 2个传感器的噪声均值

试验时, 将2个传感器安装在距离200 cm的同一个水平面上, 设置2个传感器的Z轴垂直指向上, X轴平行且指向一致。则建立1个以2个传感器中心为原点, Z轴垂直于水平面向上, X轴与传感器X轴一致的直角坐标系。试验所建立的坐标系如图1所示。图中, 给出了目标运动的3条轨迹, 出于篇幅限制这里给出目标按照轨迹2运动时的试验结果。轨迹2的起点和终点坐标分别是(150, 150, 23) cm, (-150, -150, 23) cm, 目标的运动速度, 。

图2给出了试验的实物图, 磁偶极子目标被安装在小车上并且小车按照地面所绘制的轨迹运动。另外, 2个磁通门传感器的磁场通过电缆传送到数据采集卡。表2给出了试验使用的磁偶极子目标在坐标系中的磁矩参数。

图2 实测试验实物示意

表2 目标磁偶极子的磁矩值

试验同时使用了PF, SPPF和GMSPPF算法处理获取的数据, 以对比算法的性能。图3是目标按照轨迹2运动时, 2个磁通门传感器获取的磁场数据, 图中所示的波形是经过滤波处理后的信号。其中, 上图为1号传感器第2条轨迹的测量值, 下图为2号传感器第2条轨迹的测量值。对数据进行50次蒙特卡洛计算, 采用式(10)中的均方根误差(root mean square error, RMSE)来反映估计的精度。

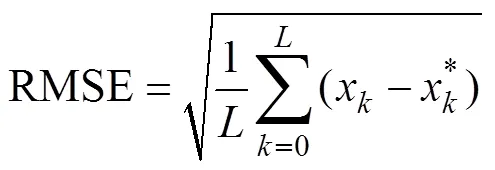
式中: 是实际状态参数值; 是状态估计参数值; 是计算数据的点数。

通过计算得到了图4~图11和表2所示的结果。图4是算法估计的目标运动轨迹和实际运动轨迹的跟踪图。可以看出, GMSPPF算法和SPPF算法均可准确地跟踪目标的运动轨迹, 但后者在轨迹的终端有些发散。图5~图11分别给出了系统状态参数的跟踪误差图, 误差是由算法估计值和参数真实值做差得到的。从图中可以看出: GMSPPF算法和SPPF算法的估计误差均可以收敛到零值附近, 明显优于PF算法; SPPF算法的磁矩参数误差大于GMSPPF算法, 并且SPPF算法的收敛速度不及GMSPPF算法; 另外, SPPF算法的执行时间是GMSPPF算法的10倍以上, 说明后者在降低前者计算量的前提下提高了前者的性能。从误差的数值可看出, GMSPPF算法的位置参数误差稳定在0.03cm左右; 速度估计误差为0.01cm/s左右; 磁矩参数的误差在106量级, 只有目标实际磁矩参数的千分之一。

表3给出了GMSPPF算法估计参数的RMSE均值和方差。表中, 均值反映了算法估计的误差大小, 而方差是算法估计误差的波动情况。

图4 偶极子轨迹跟踪结果

图5 偶极子X轴位置的跟踪误差曲线

图6 偶极子Y轴位置的跟踪误差曲线

Fig.6 Tracking error curves of dipole-axis position

图7 偶极子X轴速度的跟踪误差曲线

图8 偶极子Y轴速度的跟踪误差曲线

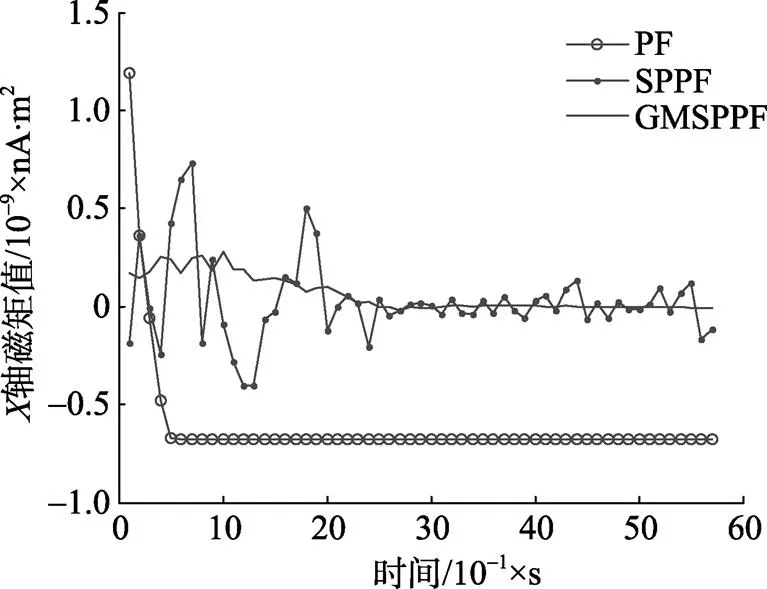
图9 偶极子X轴磁矩的估计误差曲线

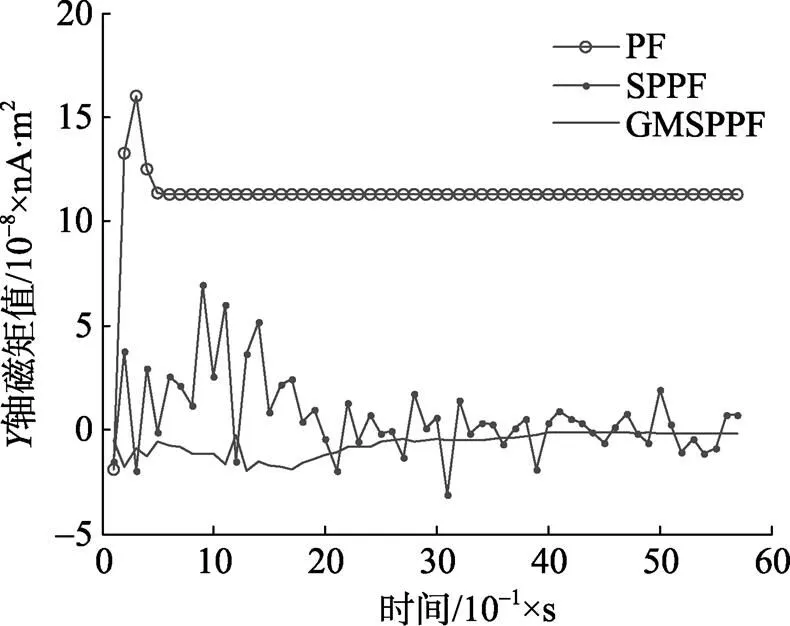
图10 偶极子Y轴磁矩的估计误差曲线

图11 偶极子Z轴磁矩的估计误差曲线

表3 高斯混合采样粒子滤波算法的均方根误差均值和标准差

3 结束语

论文给出了如何使用磁偶极子的磁场特征测量值来反演该磁偶极子的位置、速度和磁性参数的问题。应用高斯混合采样粒子滤波算法实现了磁偶极子目标跟踪。论文分析了偶极子跟踪的理论本质并建立了偶极子跟踪的状态方程模型。使用磁通门传感器和磁偶极子目标进行实测试验, 并使用了PF, SPPF, GMSPPF等算法对试验获取的数据进行计算。对比PF, SPPF算法的计算结果表明, GMSPPF算法提高了SPPF算法的性能并且降低了计算量; 成功实现了偶极子跟踪, 其位置参数误差小于0.03 cm、速度参数误差小于0.01 cm/s、磁矩参数的估计误差小于0.01%。

[1] Wahlstom N．Target Tracking Using Maxwell′s Equations [D]．Linkoping, Sweden: Linkoping University, 2010．

[2] 林春生, 龚沈光．舰船物理场[M]. 北京: 兵器工业出版社, 2007.

[3] Wahlstrom N, Callmer J, Gustafsson F. Magnetometers for Tracking Metallic Targets[C]//Processing of 13th International Conference on Information Fusion, 2010．

[4] Wahlstom N．Target Tracking Using Maxwell′s Equations [D]．Linkoping , Sweden: Linkoping University, 2010．

[5] Birsan M．Non-linear Kalman Filters for Tracking a Magnetic Dipole[C]//Processing of InternationalConference on Maritime Electromagnetic, MARELEC, 2003.

[6] Birsan M. Unscented Particle Filter for Tracking a Magnetic Dipole Target[C]//Proceedings of MTS/IEEE, 18-23 Sept, 2005, USA, IEEE, 2005: 1-4．

[7] Wynn W M．Magnetic Dipole Localization with a Tensor Gradiometer[C]//Proceedings of theInternational Conference on Marine Electromagnetic MARELEC, Brest, 1999: 295- 304．

[8] Wynn W M．Magnetic Dipole Localization with a Gradiometer: Obtaining Unique Solutions[J]．Proceedings IEEE Symposium on Geosciences and Remote Sensing, Singapore, 1997(4): 1483-1485．

[9] Rudolph M．Gaussian Mixture Sigma-point Particle Filters for Sequential Probabilistic Inference in Dynamic State- space Models[C]//Proceedings of the InternationalConf- erence on Acoustics, Speech and Signal Processing, Hong- Kong,2003: 701-704．

[10] Gupta S, Gangopadhyay R, Prati G．Accurate BER Estimation of Optical DPSK Systems Using Sum of Gaussian Approximation[C]//Proceedings of the Joint International Conference on Optical Internet and Next Generation Network, South Korea, 2006: 46-48．

[11] Julier S J, Uhlmann J K, Durrant-Whyte H F．A New Approach for the Nonlinear Transformation of Means and Covariance in Filters and Estimators[J]．IEEE Transactions on Automatic Control, 2000, 45(3): 477-482．

Magnetic Dipole Tracking Based on Nonlinear Filtering Algorithm

WU Zhi-dong, ZHOU Sui-hua, CHEN Zhi-yi

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

To realize the magnetic dipole tracking with high nonlinearity characteristic, the estimation of magnetic dipole′s position, magnetic moment, and velocity is formulated as a Bayesian estimation problem for dynamic systems. A recursive approach is proposed to evaluate the state parameter of the target. Based on the proposed method, the Gaussian-mixture sigma-point particle filter(GMSPPF) is adopted to realize the magnetic dipole tracking. The performance of the proposed method is verified through experiment. The results indicate that the proposed method can achieve higher tracking performance, and GMSPPF performs better in both estimation and computational efficiency than the particle filtering and sigma-point particle filtering algorithms.

magnetic dipole tracking; Bayesian estimation; Gaussian-mixture sigma-point particle filter algorithm

TJ630.33

A

1673-1948(2013)04-0262-06

2013-03-20;

2013-04-22.

国家自然科学基金(51109215).

吴志东(1986-), 男, 在读博士, 研究方向为磁性目标探测与识别.

(责任编辑: 杨力军)