矢量水听器阵方位估计的最佳线性融合

王绪虎, 陈建峰, 安芹力



矢量水听器阵方位估计的最佳线性融合

王绪虎1, 2, 陈建峰1, 安芹力1

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2.曲阜师范大学 物理工程学院, 山东 曲阜, 273165)

为了改善矢量水听器方位估计的性能, 研究了基于ESPRIT算法的矢量阵方位估计问题, 分析了其基本原理, 推导了该算法方位估计方差的理论公式, 得出了矢量阵ESPRIT方法估计方差较大, 且估计性能受实际目标方位影响严重。针对该方法的不足, 提出了对独立估计出的目标方位进行最佳线性融合的处理方法, 该融合算法的估计方差不大于任何一个独立估计的方差。仿真结果表明, 最佳线性融合算法提高了矢量水听器阵的方位估计精度, 降低了估计性能随目标方位变化波动的程度。

矢量水听器; ESPRIT算法; 方位估计; 线性融合

0 引言

矢量水听器是一种新型水下声传感器, 可以同步共点地拾取声场中的声压和振速信息, 相对于传统的声压水听器来说, 它增加了接收信息的种类和数量, 拓展了后置信号处理空间。矢量水听器具有良好的低频指向性, 抑制各向同性噪声等诸多优点[1-2], 为解决水声工程中的许多问题提供了新思路和方法。从上世纪90年代以来, 矢量水听器的研究已经成为水声技术领域内的一个研究热点, 并被公认为21世纪国内水声技术领域最具有发展前景的方向之一。

国外关于矢量水听器的研究起步较早, 据公开发表的文献记录, 美国和俄罗斯已经在矢量水听器的制作, 矢量信号处理理论研究和工程应用研究等方面取得了很多的成果。一批性能优越稳定的矢量阵列系统已经在民用, 军用产品中出现[3-4]。我国关于矢量水听器技术的研究起步较晚, 但在矢量水听器的制作、矢量信号处理、舰船噪声测量、声纳浮标及拖曳阵列中的应用等方面已取得丰硕的成果[5-7]。

本文针对借助旋转不变技术估计信号参数(estimation of signal parameters via rotational invariance technique, ESPRIT)方法的矢量水听器阵方位估计技术进行了深入研究, 分析表明该种处理方法具有如下特点。

1) 阵型可任意布放, 且不需分割成2个完全相同的子阵;

2)方位参数解算过程中不需要目标的频率信息;

3) 可同时实现多源的方位估计。

本文对这种处理方式的误差进行了理论分析, 针对利用振速分量直接估计方位性能较差且受声源方位影响较大的问题, 提出了最佳线性角度融合优化方法来提高测向精度, 降低误差起伏。通过计算机蒙特卡洛仿真试验验证了理论分析的正确性和所提方法的有效性。

1 矢量水听器测量模型

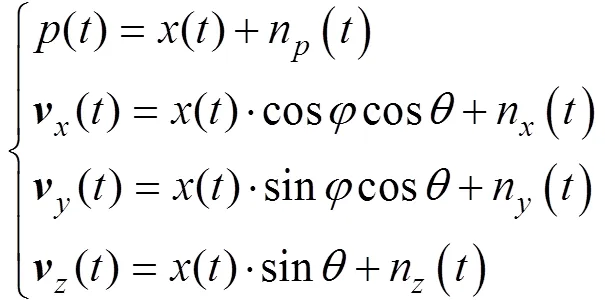
图1 振速在x, y, z轴上的投影关系

2 矢量水听器阵ESPRIT算法原理

由式(2)可以看出, 声压子阵经过旋转后变成了振速分量子阵, 子阵输出数据间的旋转矩阵只与目标的方向有关, 而与矢量水听器的空间位置和目标信号的频率无关。同时可以看到, 这种旋转保持了对应子空间的旋转不变性, 体现了ESPRIT算法的基本思想。

根据分块矩阵之间的对应关系可得

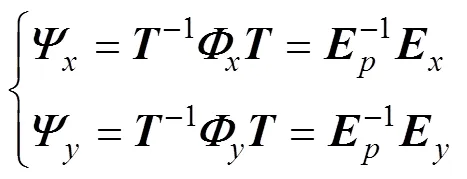
有许多解算方法可求旋转矩阵, 其中有矩阵束方法、最小二乘方法, 总体最小二乘和结构最小二乘方法等, 文献[9]和文献[10]对这些方法做了详细分析, 本文不再详述。

3 ESPRIT算法性能分析

由上式可得目标方位估计的方差分别为

上式说明了直接利用矢量阵的ESPRIT算法来估计方位的方差跟目标方位有关系, 且由于式(6)中的2个系数是小于等于1的, 因此得到方位估计性能较差。

4 目标方位的线性融合分析

数据融合的目的是寻找一个新的估计量

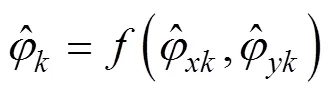
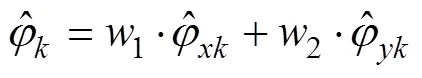
式中, E表示求数学期望。

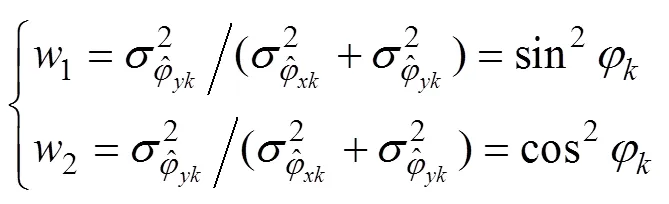
由上式可知, 最佳线性加权融合是对2个独立的变量加权, 加权参数的大小与分量的标准差成反比。误差越大, 权系数越小。且文献[11]已经证明, 以最小方差为准则的最佳线性融合所得的新估计量的误差不大于每一分量原来的估计方差。

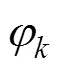
5 仿真结果与分析

图2 信噪比变化时几种算法的统计性能

图3中还可以观察到加权融合处理方法的曲线随方位角度的起伏非常小, 且基本上低于直接利用振速分量的性能曲线(图3(c)中在靠近坐标轴的方位上融合优化方法性能稍差, 这是因为此时信噪比较低, 预估计角度误差较大造成的)。这与第3~4节的理论分析结果是一致的, 充分验证了融合优化算法的有效性。

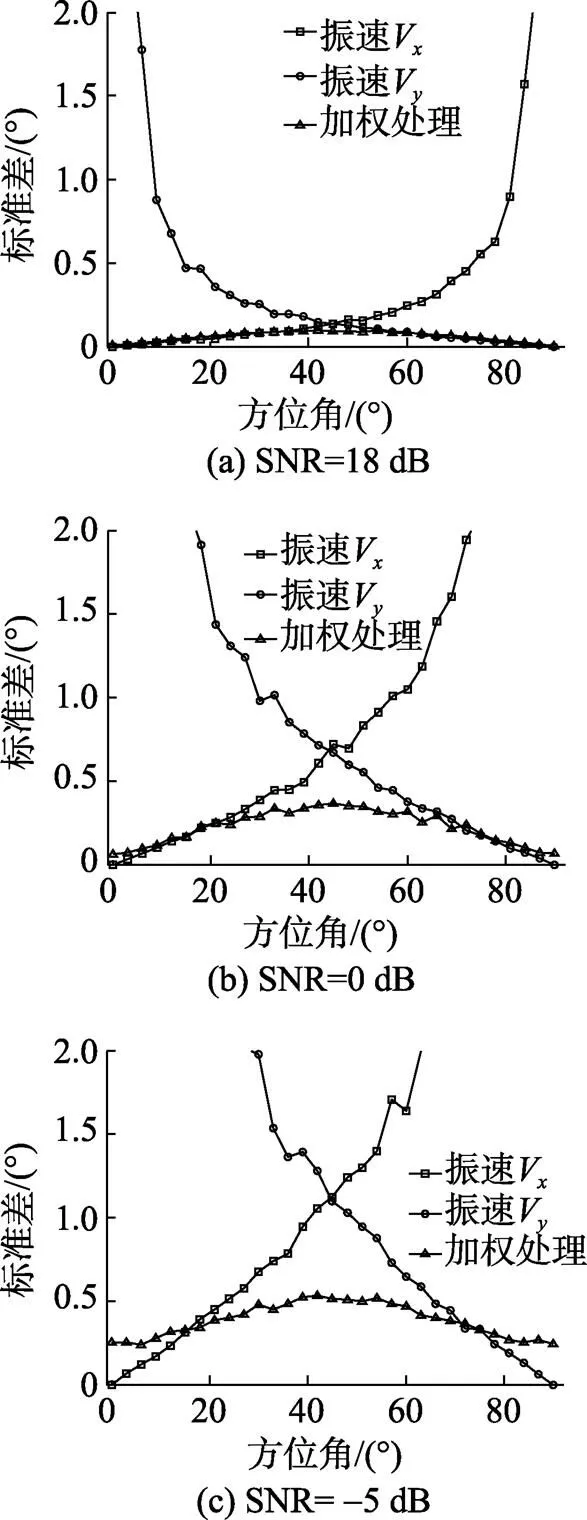
图3 方位变化时几种算法的统计性能

6 结束语

本文从理论上分析了矢量阵ESPRIT算法方位估计的误差, 仿真结果与理论结果近似吻合。结合矢量阵ESPRIT算法误差的特点, 提出了一种角度融合优化方法, 该方法不仅提高了方位估计的精度, 且对目标实际方位具有更好的稳健性。该方法具有: 1) 适用窄带和宽带信号源; 2) 可实现多源方位估计; 3) 在处理过程中对阵列形状没有要求, 且不需要划分子阵等特点, 因而存在较大的工程应用价值。

[1] Nehorai A, Paldi E. Vector-sensor Array Processing for Electromagnetic Source Localization[J]. IEEE Transaction Signal Processing, 1994, 42 (2): 376-398.

[2] Nehorai A, Paldi E. Acoustic Vector-array Processing[J]. IEEE Transaction Signal Processing, 1994, 42(9): 2481-2491.

[3] Hawhes M. Issues in Acoustic Vector-Sensor Processing[D]. New Black Text: Yale University, 2000.

[4] Rouquette R E. Towed Streamer Deghosting: USA, 7 167413 B1 [P]. 2007-02-23.

[5] 贾志富. 全面感知水声信息的新传感器技术——矢量水听器及其应用[J]. 物理, 2009, 38(3): 157-168.Jia Zhi-fu. Novel Sensor Technology for Comprehensive Underwater Acoustic Information——Vector Hydrophones and Their Applications[J]. Physics, 2009, 38(3): 157-168.

[6] 孙贵青, 杨德森, 张林, 等. 矢量水听器在水下目标低频辐射噪声测量中的应用[J]. 哈尔滨工程大学学报, 2001, 22(5): 5-9. Sun Gui-qing, Yang De-sen, Zhang Lin, et al. Application of Vector Hydrophone to Measurement of Low Frequency Radiation Noise from Underwater Target[J]. Journal of Har- bin Engineering University, 2001, 22(5): 5-9.

[7] 孙贵青, 杨德森, 张揽月. 基于矢量水听器的水下目标低频辐射噪声测量方法研究[J]. 声学学报(中文版), 2002, 27(05): 429-434. Sun Gui-qing, Yang De-sen, Zhang Lan-yue. Research on the Method for Measuring Radiated Noise by an Underwater Target in Low Frequeney Band Based on the Vector Hydro- phone[J]. Acta Acustica, 2002, 27(5): 429-434.

[8] Stoica P, Nehorai A. MUSIC, Maximum Likelihood, and Cramer-Rao Bound[J]. IEEE Transaction on Acoustics, Spee- ch and Signal Processing, 1989, 17(5): 720-741.

[9] 王永良, 陈辉, 彭应宁. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.

[10] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004.

[11] 李启虎. 独立观测资料的最佳线性数据融合[J]. 声学学报, 2000, 25(5): 385-387.Li Qi-hu. Optimum Linear Data Fusion for Independent Observation Data[J]. Acta Acustica, 2000, 25(5): 385-387.

Optimum Linear Fusion for DOA Estimation with Vector Hydrophone Array

WANG Xu-hu1, 2, CHEN Jian-feng1, AN Qin-li1

(1. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China; 2. College of Physics and Engineering, Qufu Normal University, Qufu 273165, China)

To improve the direction of arrival (DOA) estimation performance of a vector hydrophone array, the estimation of signal parameters via rotational invariance technique (ESPRIT) of a vector hydrophone array is studied. Based on analysis of vector array ESPRIT, theoretical estimation covariance formulas of vector array ESPRIT method are deduced, which bring about large estimation covariance at certain target bearing. Consequently, an algorithm of optimum linear data fusion for independent DOA estimation is proposed. Simulation results show that the proposed fusion method improves the accuracy of DOA estimation via vector hydrophone array with smaller fluctuation of the estimation covariance following target bearing.

vector hydrophone; estimation of signal parameters via rotational invariance technique(ESPRIT) algorithm; direction of arrival (DOA) estimation; linear fusion

TJ630.34; TN911.7

A

1673-1948(2013)01-0025-05

2012-05-17;

2012-06-18.

国家自然基金(60972152), 山东省高等学校科技计划(J09lg07), 西北工业大学基础研究基金(JC20100223).

王绪虎(1979-), 男, 在读博士, 讲师, 研究方向为阵列信号处理.

(责任编辑: 杨力军)