基于模糊理论的鱼雷Bayes可靠性评价方法

孟凡亮, 周徐昌, 刘天华, 刘 洪



基于模糊理论的鱼雷Bayes可靠性评价方法

孟凡亮, 周徐昌, 刘天华, 刘 洪

(海军工程大学 兵器工程系, 湖北 武汉, 430033)

在鱼雷可靠性评定中, 传统的方法是基于布尔系统理论, 较少考虑到“合格”和“不合格”之间的过度状态。为了更客观真实的评价鱼雷可靠性水平, 在模糊数学的基本理论基础上, 提出了新的合格度计算方法, 建立了一种由模糊数表示试验结果的模型, 进而提出了用Bayes方法对可靠性水平进行评定的方法, 得出了一个表示鱼雷可靠性水平的模糊区间。这种方法不仅更符合实际情况, 而且具有Bayes方法节省试验样本的优点, 算例结果表明了该方法的可行性。

鱼雷; 可靠性评定; 模糊理论; Bayes方法

0 引言

鱼雷是一种结构复杂的武器系统, 其可靠性试验包含对多种战术及性能指标项目进行考核, 试验出现的结果是随机的, 而由于对鱼雷的要求较为模糊[1], 使得准确评价其可靠性变得比较困难。传统方法只是将指标项目的测试结果判为合格和不合格两种状态。超差点法是通过将测试指标划分为合格带和多条超差带, 通过计算测试结果落入超差带的超差点数之和, 判断测试项目是否合格。超差点法是对传统方法的改进, 但是超差带之间的过度部分仍然是突变的, 并没有很好地体现“成功”和“失败”之间的缓慢过度状态, 并且得出的结果仍然是二项分布, 不足以客观地评价试验结果。在可靠性评定中, 传统的Bayes方法被广泛应用, 但是仍依赖于准确的试验结果, 不能客观准确地得到试验结果时, 评定结果会受到影响。在Bayes方法中用模糊的试验结果评定鱼雷可靠性是值得探索的方向。

模糊理论在可靠性领域的应用, 文献[1]提出了鱼雷可靠性模糊评定的概念, 将每个项目的试验结果用合格度表示, 用模糊评判模型得出每条次试验结果; 文献[2]通过设置合格度的阈值, 计算大于阈值的合格度之和, 得出成功次数, 但阈值选择的主观性比较强; 文献[3]和[4]从单元可靠性分析出发, 讨论了当单元可靠性为模糊状态时系统可靠性的评价方法。根据鱼雷可靠性试验的特点, 本文提出了将每个检测项目的合格度折合为条次合格度的方法, 在此基础上建立表示“合格”和“不合格”的模糊数模型, 将试验的总合格数用模糊数表示, 最后用Bayes方法得出了可靠性的模糊区间, 并用算例证明了这种方法的合理性。

1 指标测试结果的模糊处理

模糊化方法不再把各指标测试结果分为合格和不合格, 而是从合格状态缓慢退化为不合格状态, 这更适合认知习惯。假设航程指标要求为10000 m, 而实际测得的航程为9990 m, 此时按传统方法评定为不合格显然是不稳妥的。如果按照模糊理论的概念, 给出“大概合格”的评价显然会更加科学。定义“测试结果合格”是模糊集合, 各测试结果对应的隶属度则表示该项目的合格程度, 称为项目合格度。即将每个项目的测试结果用项目合格度表示, 而不是直接判断为合格或不合格。

鱼雷的测试项目包括性能指标和功能指标, 性能指标从合格到失败的过度状态可以线性描述, 因而可以选择梯形和半梯形分布作为隶属度分布。在鱼雷可靠性试验性能指标测试项目中有下列3种情况[5]。

1) 对于像辐射噪声这种有上限指标的项目可以用偏小型半梯形分布描述(图1-a), 合格度表达式为

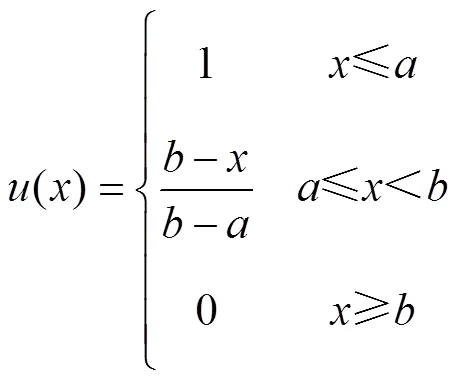
2) 对于像航程这种有下限指标的项目可用偏大型半梯形分布描述(图1-b), 合格度表达式为

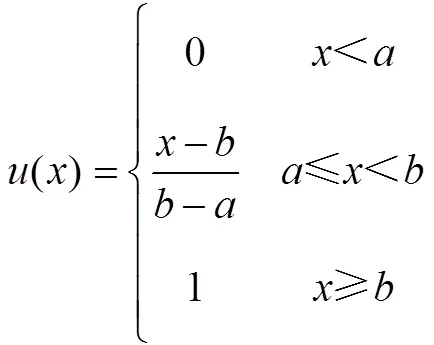
3) 对于像深度偏差这种既有上限又有下限的指标, 可以用梯形分布描述(图1-c), 合格度表达式为

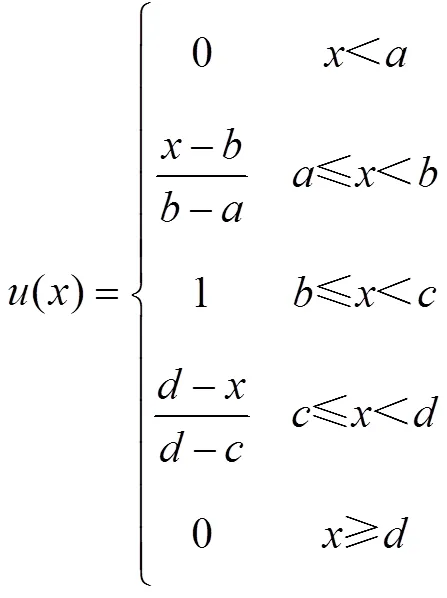
梯形分布在和之间隶属度为, 时隶属度缓慢增大, 时又缓慢变小。

功能指标的测试结果不是连续变化的, 因而选择离散隶属度分布, 将合格度离散地分成几个等级, 如图2所示, 表达式为

是否正确描述合格度的关键在于过度带的宽度和位置, 一般情况下要结合实际情况提前确定。

2 条次合格度评价模型

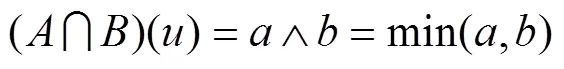
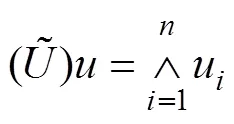
3 Bayes评定方法

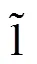
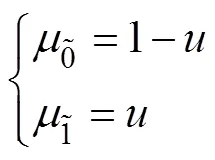
当合格度时表示“基本不合格”, 此时取模糊数, 用三元数表示为; 当合格度时表示“大概合格”, 此时取模糊数, 用三元数表示为。

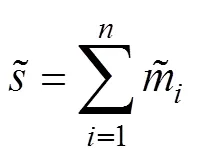
隶属度函数如图4所示。

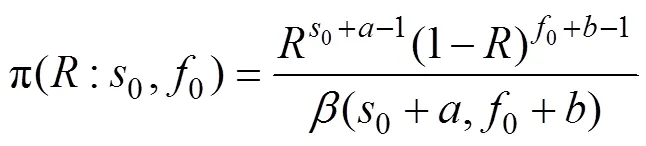
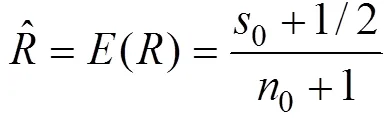
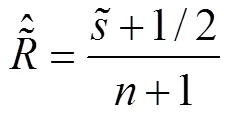
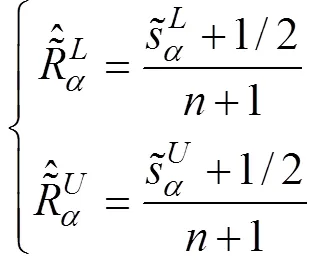
4 算例分析

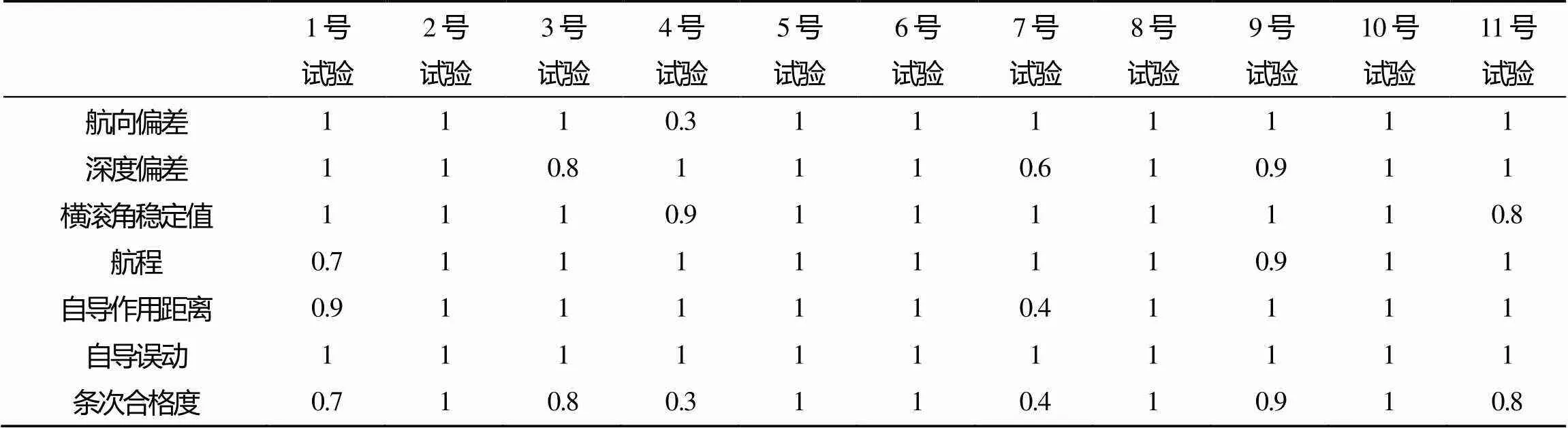
表1 试验数据和评定结果

5 结束语

不断探索新的方法, 利用新的理论来提高鱼雷可靠性评价的精度是科研工作者不断追求的目标, 鱼雷可靠性评定技术直接关系到鱼雷的研制和使用。本文利用模糊数学的基本理论结合鱼雷试验的特点和要求, 在评定方法上做了有益的探索。文中提出了试验结果的评判方法并引入基于模糊理论的Bayes方法, 对鱼雷可靠性评定技术的进步起到了推动作用。

[1] 周春明. 鱼雷试验评定模型研究[J]. 鱼雷技术, 2008, 16 (4): 3-9. Zhou Chun-Ming. Novel Evaluation Model of Torpedo Test [J]. Torpedo Technology, 2008, 16(4): 3-9.

[2] 周春明. 多状态鱼雷可靠性评定方法[J]. 鱼雷技术, 2010, 18(6): 419- 421. Zhou Chun-Ming. Reliability Estimation Method of Torpedo in Multimode Condition[J]. Torpedo Technology, 2010, 18(6): 419-421.

[3] Wu H C. Bayesian System Reliability Assessment Under Fuzzy Environments[J]. Reliability Engineering and System Safety, 2004, 83(3): 277-286.

[4] 李执力, 杨鸣, 许智辉. 基于模糊理论的武器系统可靠性分析和评价[J]. 火力与指挥控制, 2004, 29(3): 102-104. Li Zhi-li, Yang Ming, Xu Zhi-hui. Weapon System Reliability Analysis and Appraisal Based on Fuzzy Theory[J]. Fire Control & Command Control, 2004, 29(3): 102-104.

[5] 董玉革. 机械模糊可靠性设计[M]. 北京: 机械工业出版社, 2000.

[6] 杨纶标, 高英仪. 模糊数学原理及应用[M]. 广州: 华南理工大学出版社, 2005.

[7] 周泉源, 翁朝曦. 可靠性评定[M]. 北京: 科学出版社, 1990.

[8] 蔡洪, 张士峰, 张金槐. Bayes试验分析与评估[M]. 长沙: 国防科技大学出版社, 2004.

ABayesian Reliability Assessment Method for Torpedo Based on Fuzzy Theory

MENG Fan-liang, ZHOU Xun-chang, LIU Tian-hua, LIU Hong

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

Conventional Boolean algebra-based reliability assessment methods for a torpedo consider little transition state between ‘qualified’ and ‘unqualified’. In order to assess the reliability level of a torpedo more objectively and exactly, a novel reliability assessment model is put forward on the basis of fuzzy mathematics, in which test results are represented by fuzzy numbers. Then the Bayes method is adopted in assessment of reliability level to obtain a fuzzy zone indicating reliability level of a torpedo. This method is more practical and shows a saving in test samples. Feasibility of the present method is verified by an example.

torpedo; reliability assessment; fuzzy theory; Bayes method

TJ630; TB114.3

A

1673-1948(2013)01-0006-04

2012-06-13;

2012-08-31.

孟凡亮(1988-), 男, 在读硕士, 研究方向为装备可靠性评定.

(责任编辑: 陈 曦)