一类非自治两种群浮游生物模型的概周期解
林玉花,王海娜,陈婉琳
(福州大学数学与计算机科学学院,福建福州350108)
一类非自治两种群浮游生物模型的概周期解
林玉花,王海娜,陈婉琳
(福州大学数学与计算机科学学院,福建福州350108)
考虑一个非自治的浮游植物两种群竞争模型,通过利用微分方程比较原理和构造适当的Lyapunov函数,获得了一组保证系统存在唯一的全局渐进稳定的概周期解的充分性条件。数值模拟表明了结果的可行性。
浮游植物;竞争;毒素;持久性;概周期解
研究如下模型
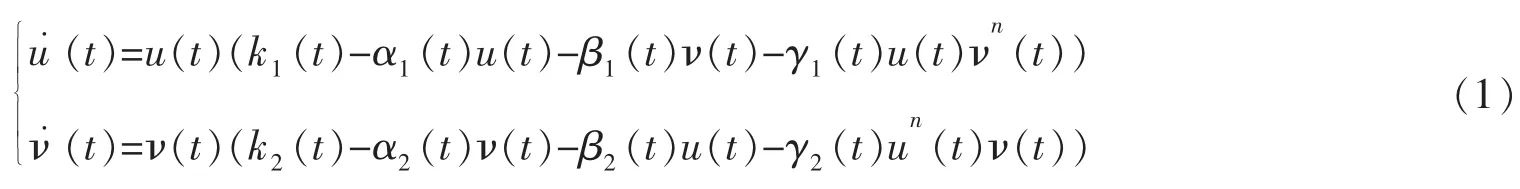
的持久性及概周期解的存在性、唯一性和稳定性,其中u(t),ν(t)分别表示两竞争的浮游植物种群在任意时刻t的种群密度,n是正整数。系统(1)的系数满足条件:
(H1)ki(t),αi(t),βi(t),γi(t),i=1,2是具有正的上下界的连续概周期函数。
基于生态学含义,假设系统(1)的解(u(t),ν(t))T满足的初值条件

学者们对毒素已经进行了深入的研究[1-5],尤其对上述模型n=1的情形进行了更为详细的研究,获得了很多很好的成果。事实上,1974年,文[1]在假设系数为正的常数下,尝试使用上述模型来刻画两种群互相释放毒素的竞争模型,但是未对模型展开研究。1996年,文[2]对文[1]中的模型的正平衡点稳定性情况进行了详尽的研究;但是较少有学者对n=2的情形展开研究。文[3]提出一类两种群竞争模型,毒素项用非线性形式γ1u2ν2来刻画,且另外一个种群不会释放毒素(γ2=0),他们认为这种模型的数值模拟图更接近实际测得的实验数据。注意到文[3]主要结果的证明有错误的,文[4]中给出了保证系统正平衡点全局稳定的充分性条件。注意到哪怕是对n=2,γ2≠0的情形至今尚未有学者进行研究,更不用说n是任意整数的情形了。因此这方面的研究还有待进一步深入展开。此外,本研究组认为合理的假设应该是两个种群均能互相释放毒素,从而用系统(1)能较好地刻画这一假设。
1 持久性
易知系统(1)的任意满足初值条件(2)的解是正的。
引理1[6]若a>0,b>0且当t≥t0和x(t0)>0时有(t)≥(≤)x(b-ax),则有

证明由条件(H2)知道存在足够小的ε>0使得

由系统(1)的第一个方程有
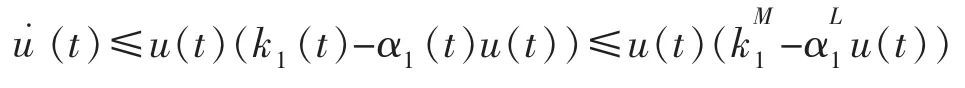
由引理1有

类似地,由系统(1)的第二个方程可得

由(4)和(5)可知,对上述ε>0,存在足够大的T>0,使得当t>T时有

由(6)的第二个不等式及系统(1)的第一个方程可知,当t>T时有

由(3)的第一个不等式和引理1有

在(7)式令ε→0有

当t>T时,由系统(1)的第二个方程及与(6)~(8)同样的分析方法有

由于Mi,mi,i=1,2是跟系统的解无关的正常数,故在条件(H2)成立的情况下,满足初始条件(2)的系统(1)是持久的。
定理2假设条件(H2)成立,此外下列条件(H3):

成立,则系统(1)是全局渐进稳定的。
证明设(u(t),ν(t))T和(u*(t),ν*(t))T是系统(1)的任意两个满足初始条件(2)的正解,由定理1可知,存在T>0,使得对∀t>T,有

沿着系统(1)的正解计算V1(t)的导数有

其中θ=min{Δ1,Δ2},对上式两端从T到t积分可得

从而有

定理2证毕。
2 概周期解
定理3若(H1)及定理2的条件成立,则系统(1)存在唯一的正概周期解,且该解是全局渐进稳定的。
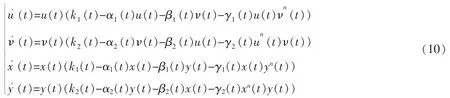
假设(U(t),X(t))T=(u(t),ν(t),x(t),y(t))T,(U1(t),X1(t))T=(u1(t),ν1(t),x1(t),y1(t))T是系统(10)
在K×K上的任意两个不同的解,其中

定义r=‖U-X‖,则mr,Mr为单调递增的正定函数;证明存在常数L>0使得

成立。事实上,当t>T时,由微分中值定理及绝对值的性质有成立。

由式(9)及式(12),(13)立即可得

3 数值模拟
给出一个例子来说明本文主要结果的可行性。

从而系统(16)满足定理3条件,有唯一的一致渐进稳定的概周期解,图1表明此结果的可行性。

图1 系统(16)满足初值条件(2.21,2.40)T,(2.01,2.30)T及(1.80,2.10)T解(u(t),ν(t))T的模拟图
4 结论
由条件(H2),发现系统的持久性与毒素无关。通过构造Lyapunov函数、采用高次项因式分解和放缩的方法,得到系统(1)在条件(H1)、(H2)、(H3)成立时存在唯一的全局渐进稳定的概周期解。但仍然有许多有趣且具有实际意义的问题未解决,比如这些条件均为充分性条件,对于该结论的必要条件是否一定与毒素有关,仍不得而知。再比如当n是有限的正实数时,系统是否仍然有唯一的全局渐进稳定的概周期解,如果有,那么条件是否一样?对于这些问题,有待以后研究。
[1]MAYNARD-SMITH J.Models in ecology[M].Cambridge:Cambridge University Press,1974.
[2]CHATTOPHADYAY J.Effect of toxic substa nces on a two species competitivesy[J].Ecol Model,1996,84:287-289.
[3]BANDYOPADHYAY M.Dynamical analysis of a allelopathic phytoplankton model[J].J Biol Syst,2006(14):205-217.
[4]林玉花,陈凤德,王海娜,等.一类非自治两种群浮游生物相克模型的持久性和全局吸引性[J].沈阳大学学报,2012,24(6):7-10.
[5]王光菊,杜鹏,廖新元.具免疫应答时滞乙肝病毒的数学模型[J].三明学院学报,2012,29(2):9-16.
[6]CHEN F D,LI Z,HUANG J Y.Note on the permanence of a competitive system with infinite delay and feedback controls[J].J Comput Appl Math,2005,180:33-49.
[7]何崇佑.概周期微分方程[M].北京:高等教育出版社,1992.
Almost Periodic Solutions of a Non-autonomous Two Species Phytoplankton Model
LIN Yu-hua,WANG Hai-na,CHEN Wan-lin
(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China)
A non-autonomous two species allelopathic phytoplankton model is considered in this paper.By applying comparison theorem of differential equation and constructing a suitable Lyapunov function,a set of conditions which ensure the existence of an unique and globally asymptotically stable almost periodic solutions are obtained.Numeric simulation shows the feasibility of main results in this paper..
phytoplankton;competition;toxicity;permanence;almost periodic solution
O175.14
A
1673-4343(2013)02-0006-06
2012-12-09
福建省自然科学基金(2011J01007);福建省科技创新平台计划项目(2009J1007)
林玉花,女,福建厦门人,硕士研究生。研究方向:生物数学。

