反对合矩阵的相似对角化

黄益生，陈椰婷

（三明学院信息科学学院，福建三明365004）

反对合矩阵的相似对角化

黄益生，陈椰婷

（三明学院信息科学学院，福建三明365004）

反对合矩阵；反对合变换；矩阵;相似关系；分类

几何平面V2上绕原点按逆时针（或顺时针）方向旋转90°的旋转变换σ无疑是很有用的。这样的变换满足条件σ2=-ι，这里ι是V2上的恒等变换。用矩阵的语言，上述条件等价于存在实数域上的一个2阶方阵A，使得A2=-I，这里I是2阶单位矩阵。这样的矩阵A就是一个2阶反对合矩阵。一般地，满足条件A2=-I的n阶方阵A称为一个n阶反对合矩阵［1］。对于数域F上的一般线性空间，其上的线性变换σ，如果满足条件σ2=-ι，那么称σ为一个反对合变换［2］。从上述旋转变换不难看出，在矩阵论中，反对合矩阵也是一类很有用的矩阵。在文献［1］中，作者讨论了反对合矩阵的一系列基本性质，它们类似于对合矩阵的相应性质。在文献［2］中，作者给出了反对合矩阵与反对合变换之间的关系。但是经查阅各种文献（包括网上搜索），笔者未发现有关反对合矩阵的其它资料。

本文将在文献［1－2］的基础上，进一步讨论反对合矩阵的一些性质。主要结果如下：

（1）在复数域上每一个反对合矩阵都可对角化，并且全体n阶反对合复矩阵按矩阵的相似关系进行分类，一共可以分成n+1类。

（2）在实数域上不存在奇数阶反对合矩阵，并且每一个偶数阶反对合矩阵都不可对角化，但是每一个2n阶反对合矩阵都相似于准对角矩阵diag{J1，J2，…，Jn}，这里

因而全体2n阶反对合矩阵按实矩阵的相似关系进行分类，只有一种类型。

（3）指出了非零偶数维实线性空间上的反对合变换有无穷多个。

首先讨论复数域上的反对合矩阵，本文有关的术语和结论将引用文献［3－4］。

定理1在复数域上每一个n阶反对合矩阵A都可对角化。

证明已知A是复数域上的一个n阶反对合矩阵，那么A2=-I，即A2+I=O（这里I是n阶单位矩阵），所以x2+1是A的一个零化多项式，因此A的最小多项式只能为下列3个多项式之一：x-i，x+i，x2+1。显然，不论哪一种情形，A的最小多项式不可能有重根。又已知在复数域上一个方阵是可对角化的当且仅当它的最小多项式没有重根，因此A是可对角化的。

由证明可见，反对合矩阵的最小多项式，其根只能为虚数i或-i。已知每一个方阵的最小多项式与特征多项式有相同的复根（重数可以不同），那么在复数域上反对合矩阵的特征值只能为i或-i，但是在实数域上反对合矩阵没有特征值。

设A与B是复数域上的两个n阶反对合矩阵。令λ1，λ2，…，λn与μ1，μ2，…，μn分别是A与B的n个特征值。根据定理1，A相似于diag{λ1，λ2，…，λn}且B相似于diag{μ1，μ2，…，μn}。已知两个对角矩阵diag{a1，a2，…，an}与diag{b1，b2，…，bn}是相似的当且仅当它们的主对角线元素b1，b2，…，bn是a1，a2，…，an的一个排列。由于A与B的特征值只能为±i，当λ1，λ2，…，λn与μ1，μ2，…，μn这两组特征值中含虚数i的个数相同时，A与B是相似的，否则它们不相似。由此可见，在复数域上全体n阶反对合矩阵按矩阵的相似关系进行分类，一共可以分成n+1类，并且可以选取diag{iIp，-iIn-p}作为特征值i的个数都是p的那一类的代表（p=0，1，2，…，n）。

下面讨论实数域上的反对合矩阵。

设A是实数域上的一个n阶反对合矩阵，则A的特征多项式fA（x）是一个n次实系数多项式。如果n是奇数，那么fA（x）至少有一个实根，因而A必有特征值。另一方面，根据前面的讨论，在实数域上，A没有特征值，这就出现一个矛盾，因此n不可能是奇数。这就得到命题1。

命题1在实数域上不存在奇数阶的反对合矩阵。

可是对任意偶数2n，必存在2n阶反对合矩阵。

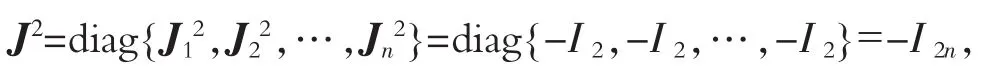
因此J是一个反对合矩阵。

已知反对合矩阵的特征多项式，其根只能为虚数i或-i，那么在实数域上每一个反对合矩阵都不可对角化。然而有定理2。

定理2设A是实数域R上的一个2n阶方阵。令J=diag{J1，J2，…，Jn}，其中

则A是反对合的当且仅当它相似于准对角矩阵J，即存在一个2n阶可逆实矩阵T，使得

证明设A是R上的一个2n阶反对合矩阵。根据定理1的证明，x2+1是A的一个首一零化多项式。因为x2+1在实数域上不可约，所以它是A的最小多项式。已知每一个方阵的最小多项式与特征多项式有相同的复根（重数可以不同），那么A的特征多项式为fA（x）=（x2+1）n。

把A看作复数域C上的矩阵，那么A的特征值为i与-i，并且A是可对角化的（定理1），所以特征值i与-i的几何重数都是n。设ξ1，ξ2，…，ξn是A的属于特征值i的n个线性无关特征向量，则Aξk=iξk（k=1，2，…，n）。令ξk是把ξk的2n个分量依次换成相应的共轭复数所得的向量，则ξk是C2n中的一个非零向量，并且iξk=-iξk。已知Aξk=iξk，那么Aξk=iξk，所以Aξk=-iξk。因为A是一个实矩阵，容易验证，Aξk=Aξk，因此

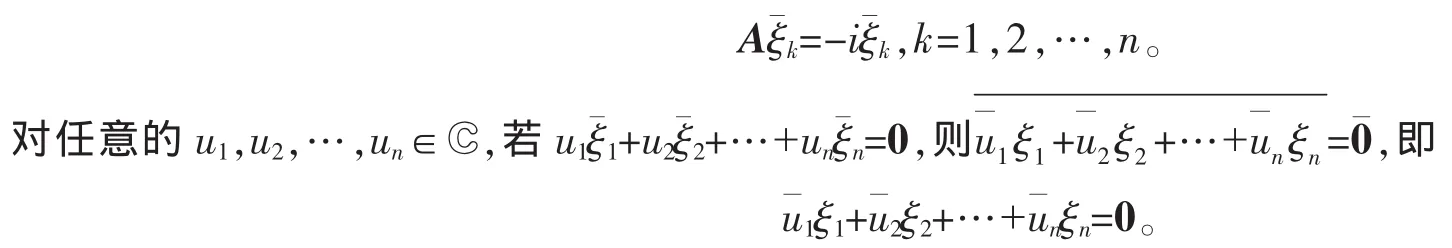
又因为ξ1，ξ2，…，ξn线性无关，所以u1，u2，…，un全为数零，即u1，u2，…，un全为数零。这表明，ξ1，ξ2，…，ξn是A的属于特征值-i的n个线性无关特征向量。已知属于不同特征值的特征向量必线性无关，那么ξ1，ξ1，ξ2，ξ2，…，ξn，ξn构成复数域上2n元列向量空间C2n的一个基。

再令αk=ξk+ξk且βk=i（ξk-ξk），则αk，βk∈R2n（k=1，2，…，n）。因为

这就证明了，在实数域上，A相似于准对角矩阵J。

反之，设A相似于J，则存在一个2n阶可逆实矩阵T，使得A=TJT-1。于是A2=TJ2T-1。因为J2= -I，所以A2=-TT-1，即A2=-I，因此A是反对合的。

上述定理表明，在实数域上全体2n阶反对合矩阵按矩阵的相似关系进行分类，只有一种类型，并且可以选取定理中的准对角矩阵diag{J1，J2，…，Jn}作为这种类型的矩阵的代表。因此实数域上由全体2n阶反对合矩阵组成的集合可以表示成｛Tdiag{J1，J2，…，Jn}T-1|T是2n阶可逆实矩阵｝，

特别地当n=1时，上述集合（即由全体2阶反对合实矩阵的集合）变成｛TJT-1|T是2阶可逆实矩阵｝，

讨论反对合变换，见例2。

例2设V是数域F上的一个2n维线性空间，并设α1，β1，α2，β2，…，αn，βn是V的一个基，则V中的每一个向量ξ可以表示成

在文献［2］中，作者证明了，反对合变换与它在某个基下的矩阵之间有如下关系。

定理3［2］设V是数域上F的一个n维线性空间，并设σ是V上的一个线性变换，则σ是反对合的充要条件为它在V的一个基下的矩阵是反对合的。

注意到有限维线性空间V上的一个线性变换是可对角化的当且仅当它在V的一个基下的矩阵是可对角化的，根据定理3和定理1，下列推论成立。

推论1设V是复数域上的一个n维线性空间，并设σ是V上的一个线性变换。若果σ是反对合的，那么它是可对角化的。

根据定理3，命题1和定理2，下列两个推论成立。

推论2设V是实数域上的一个奇数维线性空间，则V上的一个线性变换都不是反对合的。

推论3设V是实数域上的一个2n维线性空间，并设σ是V上的一个线性变换，则σ是反对合的当且仅当存在V的一个基，使得σ在这个基下的矩阵为准对角矩阵J=diag{J1，J2，…，Jn}，其中

假定推论3中的反对变换σ在基α1，β1，α2，β2，…，αn，βn下的矩阵为J。容易看出，

令Wk是由αk与βk生成的子空间，即Wk=L（αk，βk），则dimWk=2（k=1，2，…，n），并且

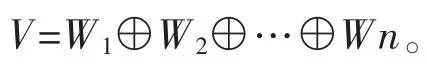
其次，对任意的ξ=xkαk+ykβk∈Wk，由于因此Wk是σ的一个不变子空间（k=1，2，…，n）。这就得到下一个推论。

推论4设V是实数域上的一个2n维线性空间，并设σ是V上的一个反对合变换，则V可以分解成σ的n个2维不变子空间W1，W2，…，Wn的直和。

推论3表明，2n维实线性空间V上的每一个反对变换σ都是例2中的变换，即存在V的一个基α1，β1，α2，β2，…，αn，βn，使得σ可以表示成

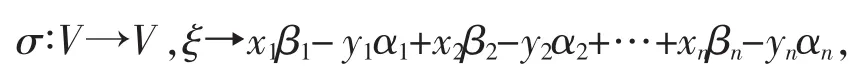
其中（x1，y1，x2，y2，…，xn，yn）是向量ξ关于上述基的坐标。

已知一个线性变换在两个基下的矩阵必相似，又已知全体2n阶反对实矩阵组成的集合恰好是与J相似的所有2n阶实矩阵组成的集合，这里J是推论3中的准对角矩阵。根据推论3，对于2n维实线性空间V上的一个反对合变换，它在V的全体基下的矩阵组成的集合恰好是全体阶2n反对合矩阵组成的集合。

根据本文开头部分或例2，存在几何平面V2上的反对合变换，那么这样的变换唯一吗？一般地，非零偶数维实线性空间上的反对合变换有几个？

例3设α，β是几何平面V2的一个基。令

则每一对αn，βn都是V2的一个基。对任意的ξ∈V2，令（xn，yn）是向量ξ关于基αn，βn的坐标，则ξ= xnαn+ynβn。构成一个映射序列如下：

根据例2，每一个σn是V2上的一个反对合变换。显然σn（αn）=βn。因为αn=α且βn=nβ，所以σn（α）= nβ。类似地，有σm（α）=mβ。由于β不是零向量，当m≠n时，有mβ≠nβ，因此σm（α）≠σn（α），故σm≠σn。这表明，反对合变换序列σ1，σ2，…，σn中任意两个不同的项都不相同，因而V2上的反对合变换有无穷多个。

这就得到非零偶数维实线性空间上的反对合变换也有无穷多个。

［1］邹本强.对合矩阵和反对合矩阵的若干性质［J］.威海职业学院学报，2007（2）：88－89.

［2］赵巧玲.欧氏空间Rn上的三种变换［J］.宝鸡文理学院学报，2002，22（1）：41－42.

［3］张禾瑞，郝鈵新.高等代数［M］.4版.北京：高等教育出版社，1999.

［4］丘维声.高等代数［M］.北京：高等教育出版社，1996.

On Problem for Similar Diagonalization of Anti-involutory Matrices

HUANG Yi-sheng,CHEN Ye-ting
(School of Information Engineering,Sanming College,Sanming 365004,China)

anti-involutory matrix;anti-involutory transformation;o matrices;similar relation;classification

O151.21

A

1673-4343（2013）02-0001-05

2013-01-20

福建省教育厅高等学校教学质量工程资助项目（ZL0902/TZ(SJ)）

黄益生，男，福建龙岩人，教授。研究方向：代数。