主分量分析在激励源识别中的应用研究

董建超，杨铁军，李新辉，代 路

机械系统的激励源识别对于系统优化设计、声振控制及故障诊断等方面有着重要的意义。实际机械设备趋于复杂化和联合化，传感器采集的信号往往是多个振动源耦合的结果，这使得振动信号的分析过程尤为困难。这时，基于统计理论的盲信号处理方法便显现出其优越性。盲信号处理方法在激励源特性未知以及传递通道先验知识不足的情况下，以信号的统计特征为评价标准，仅仅利用采集的混合信号来估计源信号并辨识传递通道特性。然而我们所采集的信号往往数据量庞大，如何进行数据压缩并保留有效信息，成为盲信号处理中需要首先解决的问题。

主分量分析(Principal Component Analysis，PCA)是盲信号处理中非常有效的预处理方法［1－5］，由于算法简单实用，被广泛应用于数据压缩、特征提取和去除噪声等方面。Sutton［6］应用PCA对汽车悬架振动进行了分析，讨论车内噪声来源并进行主动控制。Cho等［7］结合PCA与传递路径分析进行了多源环境下的输入识别。Serviere等［8～9］应用改进的 PCA方法进行数据的降噪与白化预处理。相关文献中应用PCA方法时，往往根据经验确定主分量贡献率阈值(例如90%)来进行不相关源数的上界估计［1－2］。如何定量的截取主分量，分析PCA的影响因素，具有重要的实际意义。

针对上述问题，本文引入邻阶分量信噪比(Signal Noise Ratio，SNR)作为主分量截断的依据，通过算例仿真研究了混合矩阵条件数对PCA识别结果的影响。当PCA应用于机械系统激励源识别时，混合矩阵对应为系统的频率响应函数矩阵，激励点位置、测点位置与系统固有频率都会对频响矩阵的条件数产生影响。针对工程中的激励源，分析其线谱特征对PCA识别结果的影响。最后进行了简支梁结构激励源数目识别实验，验证了PCA不相关激励源数目识别的效果。

1 PCA几何阐释及原理

1.1 PCA几何阐释

PCA基于信号的二阶统计特性，将原始变量投影到坐标互相正交的新坐标系，使得具有最大方差的变量集中到新坐标系的少数几个坐标轴上［1］，从而在数据信息丢失最少的原则下，用少数新的变量替代原来的多维变量。图1以二维数据为例给出了主分量分析的几何解释。图1(a)为原始数据散点图，可以看出数据沿原始坐标系的x轴和y轴方向并不具有最大方差，数据存在冗余。图1(b)给出方差随坐标轴旋转角度变化的曲线，当坐标轴旋转至方差对应的峰值，即x'y'坐标系时，数据沿x'轴的分量方差达到峰值，包含了原始数据的大量信息。截取沿x'轴方向的分量即实现了原始数据的压缩处理。

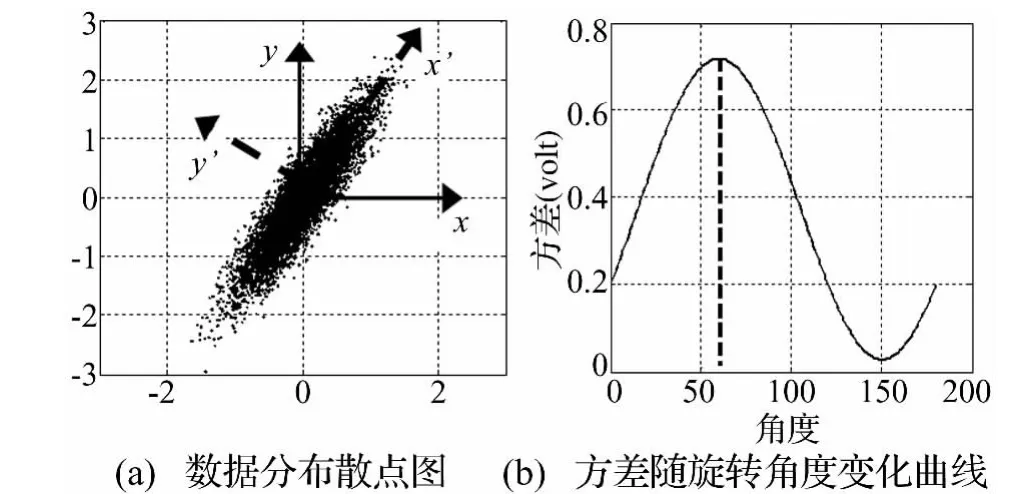
图1 PCA在几何上的解释Fig.1 Geometrically illustration of PCA

1.2 主分量求解

假设存在噪声n的条件下，混合信号x由信源信号 s经矩阵 A 混合得到［2－3］，即:

假设信源数目为m且相互之间不相关，则信源的协方差矩阵 Rs=ssT=E=Diag［e1，e2…em］，为 m 维对角方阵，对角线元素为各个信源的方差，表征信源信号的能量。δn表示噪声对信源造成的干扰。假设噪声为不相关的随机噪声，则噪声的协方差矩阵δRn=δnδnT=N=Diag［μ1，μ2…μm］，亦为 m 维对角方阵，对角线元素为各个干扰成分的方差，表征干扰成分的能量。假定测点数目为n且n≥m，即混合系统为恰定或者超定系统。对混合矩阵A进行奇异值分解［1］:

式中:上标T代表转置，U和V是奇异值分解中的左右奇异阵，且分别是p维和q维正交归一方阵，即UTU=UUT=I，VTV=VVT=I;Σ为n×m维准对角阵，其准对角线元素σi(i=1，…m)是矩阵A的各阶奇异值，且按照降序排列。

x的协方差矩阵为:

式中:ΣΣT(E+N)为m维对角阵，对角线元素为Rx的特征值，且前m个对角线元素按降序排列，其余n－m个元素为零。左奇异阵U中的列向量为Rx的特征向量。

将UT左乘x，得:

计算y的协方差矩阵:

可见Ry为对角阵，说明上述变换去除了x的相关性。y的各行向量称为主分量，协方差矩阵的各阶特征值反映了各阶主分量的能量。对主分量进行截断，舍弃能量很低的分量，可实现数据的降维压缩和信源数目的判定。

2 算例仿真及分析

根据式(5)可知，信源信号能量的差异、噪声干扰的大小以及不同的混合矩阵，都会对PCA的结果产生影响。本节主要进行信源能量均等且存在弱噪声的情况下的PCA算例仿真，并分析混合矩阵条件数的大小对分量截断产生的影响。

2.1 PCA分量截断

本节针对式(1)所示模型进行PCA仿真。其中:信源信号s为两个独立的均匀分布且具有单位方差的随机噪声信号;A=［1.8，－0.3;1.1，－0.9;－0.2，1.3］为3×2维的混合矩阵，矩阵条件数为 1.92;噪声n为三个与信源不相关且方差为0.01的随机噪声。

对混合信号x进行主分量分析，得到主分量y=［y1，y2，y3］T。混合信号和各阶主分量的方差及相关系数绝对值如表1所示。由表1可以看出，各混合信号之间存在一定的相关性。进行主分量分析后，各阶分量间相关系数变为0，去除了相关性并且各阶分量按照方差大小进行了排序。

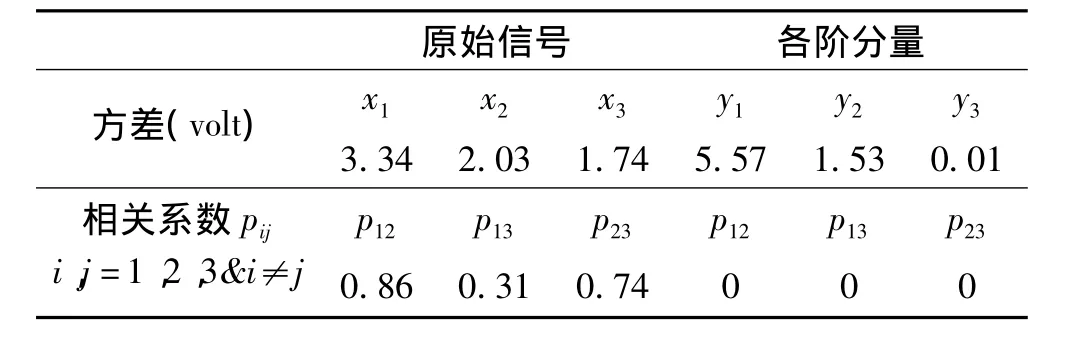
表1 方差及相关系数Tab.1 Variances and correlation coefficients

结合主分量贡献率g，引入邻阶分量信噪比来综合分析，进行分量的截断。前r阶主分量的贡献率、第i阶与第i+1阶主分量的邻阶分量信噪比分别由式(6)及式(7)计算。按照相关文献的经验［1］，本文取 g≥0.9，即当贡献率超过90%时，判定前r阶分量包含数据样本的能量。当邻阶分量信噪比很高时，说明较小的分量可作为噪声被截断。

上述算例中，一阶分量的贡献率为78.35%，前两阶分量的贡献率达到99.86%;一、二阶信噪比为5.61 dB，二、三阶信噪比为21.75 dB。从而得出结论:不相关信号源的数目为2个，截取前两阶分量可以达到降低数据维数和减少冗余的目的。

2.2 混合矩阵条件数的影响

对于矩阵A，条件数定义如下［1］:

其中:A+1=［AHA］－1AH，为A的伪逆阵。‖·‖表示矩阵的2－范数，等于矩阵的最大奇异值。

令σmax，σmin分别为矩阵A的最大与最小奇异值，则‖A‖ =σmax，‖A+1‖ =1/σmin，可得

由式(5)可知，各阶分量的能量与混合矩阵A的奇异值的平方呈正比，又由式(9)可得，第一阶分量的能量与最后一阶分量的能量之比与条件数的平方呈正比。当混合矩阵条件数很大时，主分量贡献率会变大，一阶分量分量与最后一阶分量的信噪比也会变高，这样会导致不相关源数的错误识别，主分量截断随即失效。

当存在噪声等干扰因素时，条件数很大的混合矩阵会放大干扰对信源产生的不良影响。由式(5)可知，ΣΣTN是主分量中干扰因素所对应的部分，当条件数很大时，第一阶主分量中的噪声成分会随之放大，进行分量截断时会造成信源成分的丢失。

针对2.1节中的两个具有单位方差随机信源信号，在弱噪声条件下(噪声方差为0.01)产生100个随机混合矩阵A进行混合，使前50个矩阵的条件数在1.0～1.5之间，后50个矩阵条件数在500～1 000之间。对每次混合后的数据分别进行PCA压缩降维及源数识别。100次PCA的主分量贡献率和邻阶分量信噪比结果如图2所示。

如图2所示，当混合矩阵条件数较小时(前50次)，一阶分量贡献率在65%左右，前两阶贡献率基本达到100%，从而可以判定信源数目为2个。其中一、二阶分量信噪比在3 dB左右，二、三阶分量信噪比在22 dB左右，前两阶分量量级接近且均远高于第三阶分量。截断前两阶分量，即可在不损失数据信息的前提下实现数据的压缩。

图2 PCA仿真结果Fig.2 Simulation results of PCA

当混合矩阵条件数很大时(后50次)，一阶分量贡献率已达到100%，而且一、二阶分量信噪比就高达27 dB左右，截断前一阶分量即包含所有混合数据的能量，判定信源数为1个，会得出错误结论。此时，截断前一阶分量势必会造成数据有效信息的丢失。

可见，当混合矩阵的条件数很大时，数据压缩降维处理及源数识别会失效，所以在进行主分量分析时应避免混合矩阵条件数过大的情况。当PCA应用于实际的机械系统时，混合矩阵对应为系统的传递函数矩阵，情况变得更为复杂。下面将对机械系统中PCA激励源识别问题进行分析。

3 频域下振动响应主分量分析

机械振动在传播过程中往往存在着耦合以及延迟等诸多效应，振动响应往往由多个激励源卷积混合而成。对于稳态过程的振动响应，可以在时域或者频域内进行PCA激励源识别［5］。时域法利用信号整体时间历程的统计特性，处理过程相对简便。比较而言，频域法能够在各个频段去除相关性，更有利于定量分析。因此，本文在频域下应用PCA识别机械系统激励源数目。

3.1 频域下机械系统PCA模型

对于多输入多输出的机械振动系统，假定激励数为m，响应数为n，频域下的响应为:

式中:ω为频域内各个频率值，xi(ω)表示第i个响应的傅里叶变换，hij(ω)表示第i个响应点与第j个激励点之间的传递函数，频域下对应为系统的频率响应函数，fj(ω)表示第j个激励的傅里叶变换。采用矩阵形式表示如下:

式中:

分别为系统的响应频谱、激励力频谱和频响函数矩阵。机械系统通常可近似为粘性阻尼系统，由模态分析理论，频率响应函数hij(ω)可表示为:

式中:r为系统模态阶数，ωr、ξr、φr(L)分别为系统的 r阶固有频率、阻尼系数和振型函数，Lxi和Lfj分别为第i个响应点与第j个激励点对应的位置。响应的功率谱密度矩阵为:

对SX进行特征值分解，特征值λi(ω)反映频域内各阶分量的能量。截取特征值的阶数，即为PCA识别的不相关源数目。

为了保证PCA结果的有效性，希望频响函数矩阵的条件数不要过大。由hij(ω)的表达式(13)可知，频响矩阵与激励点位置、测点位置和系统的固有频率有关。下面分别分析这些因素对频响矩阵条件数的影响。

3.2 不良激励位置与测点位置的影响

由式(13)中的分子项可知，系统的频响矩阵与激励点位置和测点位置有关。如图3(a)所示，当激励源fi与fj靠近时，源的位置与各个测点位置之间的频响函数非常接近，频响矩阵H的第i列与第j列线性相关，矩阵条件数非常大，在激励源识别过程中会将两个源视作一个“组合源”来进行处理。如图3(b)所示，当响应xi与xj靠近时，各个激励源位置与两个响应测点位置之间的频响函数非常接近，频响矩阵H的第i行与第j行线性相关，条件数也会过大，使得采集的数据冗余。实际测试分析中，为了保证激励源识别结果有效并且降低测试的复杂程度，测点位置应该保持一定间隔。

图3 两种情况下的频响函数矩阵Fig.3 Frequency response function matrices of two situations

本文针对简支梁结构进行了不同激励位置与测点位置的仿真研究，结果表明当激励源位置靠近或者测点位置靠近时，PCA识别过程失效，由于篇幅所限，并未在此列出结果。

3.3 激励源特性的影响

PCA方法基于信号的不相关性，所以激励源的特性也会对识别结果造成一定的影响。工程中的激励源具有明显的线谱特征，如式(15)所示，激励源f1(t)由p个不同频率ω1i不同幅值a1i的正弦波构成，f2(t)由q个不同频率ω2j不同幅值a2j的正弦波构成:

在此分析PCA能够得到正确识别结果时，激励源需要满足的条件。

对于不同频率的正弦信号，当采样时间足够长时，其不相关性与相位无关;同频率的正弦信号，只有当相位差为π/2时，才满足不相关性［10］，如式(16)所示。

因此，当 f1(t)和 f2(t)满足 ω1i≠ω2j(∀i，j)时，两激励源互不相关。由式(13)中的分母项可知，当激励源的频率接近系统固有频率时，频响函数矩阵的条件数非常大，系统的模态响应被激发出来并占据主导地位，固有频率附近的分离结果可信度不高，激励源识别分析时应当避开。

综上所述，当激励源f1(t)和f2(t)中频率互不相等并且均不接近系统的固有频率时，PCA能够有效地识别激励源数目。

4 PCA源数识别实验

为了验证宽频范围PCA的识别效果，本文分别采用了相关的白噪声信号与不相关的白噪声信号作为激励源，进行简支梁结构的激励源数目识别实验。两种激励源激励的情况下，分别布置两个测点与三个测点，进行两点响应与三点响应的PCA激励源数目识别研究。通过测点数目与不相关源数目相等、测点数目高于不相关源数目的情况下的识别结果，来验证PCA的激励源数目识别能力。

图4 简支梁实验台Fig.4 Simply supported beam rig

简支梁实验台及测试仪器如图4所示，梁结构的材料为45 号钢，尺寸为0.64 m ×0.056 m ×0.008 m，边界条件为简支。为避免频响函数矩阵条件数过大，激励源位置相隔一定距离，前两个测点布置在两个激励点位置，第三个测点远离前两个测点。定义图中简支梁左端为坐标原点，激励点位置为:0.18 m，0.32 m;三个测点位置确定为:0.18 m，0.32 m，0.46 m。通过仿真计算理论频响函数矩阵的条件数，除结构的固有频率外，其余频域范围的矩阵条件数均较小，表明所选定的激励位置与测点位置不会对识别过程产生不良影响。加速度响应的采样频率为4 096 Hz，采样时间为4 s。采用Welch法［10］计算响应的自功率谱和互功率谱，分段数据的点数为2 048点，重叠率为50%，窗函数使用汉宁窗。

4.1 相关白噪声激励下源数识别

采用相关白噪声信号对简支梁结构进行激励，加速度响应的自功率谱密度如图5所示(其中由于第三个测点离激励位置稍远，所以其响应量级较小，但不影响识别结果)。

由图5可以看出，响应在大部分频段内相互重叠，仅仅根据响应的频谱无法得到有效的信息来识别激励源的数目。

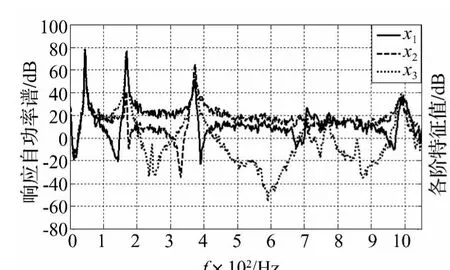
图5 相关激励源情况下的加速度响应自功率谱Fig.5 Power spectral density of acceleration responses under correlated excitation sources

图6 相关激励源情况下的功率谱矩阵特征值Fig.6 Eigenvalues of power spectral density matrices under corrlated excitation sources

分别对两点响应、三点响应构成的功率谱矩阵进行特征值分解，各阶特征值如图6所示。观察两图，第一阶特征值均比其余特征值高出近60 dB，图6(b)中二、三阶特征值比较接近，相差5 dB左右，并且数值都很小。由此说明，在测点数目与源数目相等或者高于源数目两种情况下，一阶分量量级都远高于其余阶分量，初步判定不相关激励源数目为1个。

截取特征值得到的主分量贡献率如图7所示。可以看出两种情况下截取前一阶特征值，贡献率在频域范围内接近100%，说明当测点数等于或高于源数时，一阶分量基本包含了响应信号的能量。

邻阶分量信噪比如图8所示。在固有频率处，由于结构模态响应占据主导地位，所以结果稍差。除了固有频率外的其余频域范围，一、二阶分量信噪比为30 dB左右，图8(b)中二、三阶信噪比为3 dB左右。结果表明一阶分量量级很高，可判定为激励源，二、三阶分量量级都很低，可以作为噪声进行截断。

图7 相关激励源情况下的的主分量贡献率Fig.7 Contribution coefficients of principal components under correlated excitation sources

综合图6～8可得，对于相关白噪声信号进行两点激励的情况下，当测点数目等于或高于源数目时，应用PCA进行激励源识别，结合主分量贡献率及邻阶信噪比等评价参数可以确定:不相关激励源数目为1个。

4.2 不相关白噪声激励下源数识别

图8 相关激励源情况下的邻阶分量信噪比Fig.8 SNR between neighboring components under correlated excitation sources

采用两个不相关白噪声信号对简支梁结构进行激励，加速度响应的自功率谱密度如图9所示。与4.1节图5类似，响应在大部分频段内相互重叠，仅仅根据响应的频谱无法准确识别激励源数。

分别对两点响应、三点响应构成的功率谱矩阵进行特征值分解，进行不相关源数目识别分析，各阶特征值如图10所示。固有频率处模态响应占主导地位，其余频段内，一、二阶特征值均相差5 dB左右，而图10(b)中三阶特征值与前两阶相比低近60 dB，并且数值很小。初步判定不相关激励源数目为2个。

主分量贡献率如图11所示。由图可看出截取前一阶特征值，两种情况下贡献率在除固有频率的频段内约为65～75%左右，右图中截取前两阶特征值的贡献率基本达到了100%。由此说明，测点数目与源数目相等和高于源数目两种情况下，一阶分量都未能包含响应的所有能量，而前两阶分量已经基本包含了所有能量。

邻阶分量信噪比如图12所示。图中除固有频率处较高外，一、二阶分量信噪比为3～6 dB左右;右图中二、三阶信噪比达到30 dB，说明一、二阶分量量级都很高，可判定为激励源，三阶分量量级很低，可以作为噪声进行截断。

图9 不相关激励源情况下的加速度响应自谱Fig.9 Power spectral density of acceleration responses under uncorrelated excitation sources

图10 不相关激励源情况下的功率谱矩阵特征值Fig.10 Eigenvalues of power spectral density matrices under uncorrelated excitation sources

图11 不相关激励源情况下的主分量贡献率Fig.11 Contribution coefficients of principal components under uncorrelated excitation sources

综合图10～12可知，对于不相关白噪声信号进行两点激励的情况下，当测点数等于或高于源数时，应用PCA进行激励源识别，结合主分量贡献率及邻阶信噪比，可以确定:不相关激励源数目为2个。

当测点数目增加时，相关白噪声激励、不相关白噪声激励情况下的多点响应PCA识别结果类似，前一阶或者前两阶主分量的特征值及贡献率基本不变，后几阶分量特征值和贡献率都很小，激励源数目识别结果不变。由于篇幅所限，本文未将多点响应的识别结果列出。

图12 不相关激励源情况的邻阶分量信噪比Fig.12 SNR between neighboring components under uncorrelated excitation sources

综合对比相关白噪声与不相关白噪声两种激励情况下的源数目识别结果可得:当测点数目等于或高于激励源数目时，应用PCA进行激励源识别，可以有效地分离出能量量级高的主分量作为激励源，小量级分量由于其贡献率低且邻阶分量信噪比高，可作为噪声进行截断。

5 结论

分析了混合矩阵条件数对PCA识别结果的影响，主分量贡献率、一阶分量与最后一阶分量的信噪比以及噪声干扰对信源产生的不良影响均随条件数的增大而增大，从而导致主分量截断失效。

当PCA应用于机械系统时，不良的激励点位置与测点位置情况下的分离结果以及系统固有频率附近的分离结果可信度都不高。研究了工程中激励源的线谱特征对识别结果的影响，发现各个激励源的频率互不相等并且均不接近系统的固有频率时，激励源满足不相关性条件，能够保证识别结果有效。

进行了简支梁结构激励源数目识别实验，引入邻阶分量信噪比作为主分量截取的依据，研究了测点数目等于或高于激励源数目情况下的识别能力。结果表明:在多源激励环境下，当测点数目等于或高于源数目时，对响应进行主分量分析能够准确识别不相关激励源的数目。以此为基础的预处理，能够确保激励源盲识别过程更加可靠。

［1］Jolliffe I T.Principal component analysis［M］.Springer-Verlag，New York，2002.

［2］ Comon P，Jutten C.Handbook of blind source separation:independent component analysis and applications［M］.Elsevier，USA，2010.

［3］Hyvarinen A，Karhunen J，Oja E.独立成分分析［D］.北京:电子工业出版社，2007.

［4］ Cichocki A，Amari S.Adaptive blind signal and image processing［M］.John Wiley＆ Sons，Ltd，2002.

［5］Liu X.Blind source separation methods and their mechanical application［D］.Australia:The University of New South Wales，2006.

［6］ Sutton T J.Active control of road noise inside vehicles［J］.Noise Control Eng，1994，42(4):137－147.

［7］ Cho M S，Kim K J.Indirect input identification in multisource environments by principal component analysis［J］.Mechanical Systems and Signal Processing，2002，16(5):873－883.

［8］ Serviere C，Fabry P.Blind source separation of noisy harmonic signals for rotating machine diagnosis［J］.Journal of Sound and Vibration，2004，272:317－339.

［9］ Serviere C，Fabry P.Principal component analysis and blind source separation of modulated sources for electro-mechanical systems diagnostic［J］.Mechanical Systems and Signal Processing，2005，19:1293－1311.

［10］ 胡广书.数字信号处理［M］.北京:清华大学出版社，2003.