重冰区导线断线响应及荷载取值分析

杨风利

输电线路断线会产生较大的纵向不平衡张力，会对输电线路杆塔造成瞬态冲击，使输电杆塔的内力及位移响应明显增大，导致断线档杆塔倒塌甚至引起输电线路串倒，严重影响输电线路的安全运行。因此，输电线路断线荷载及断线工况下塔线体系的动力分析与试验研究一直受到研究及设计人员的广泛关注。

输电线路导线断线数值分析研究主要集中在两方面。一是基于等线长法编制静力计算程序［1-3］，分析连续档导线断线后导线残余静态张力及悬垂串偏移量，该方法不能考虑断线过程中的冲击效应。二是采用隐式、显式动力分析方法、能量分析方法［4-10］，计算断线时输电线路动态断线张力、悬垂串偏移、杆塔位移及内力时程，研究断线冲击对导线、地线及杆塔动力响应的影响规律。

同时，国内外也开展了大量断线模拟及真型试验研究。Peyrot等［11］通过在Wisconsin试验线路段进行断线和断串试验，研究了纵向荷载特性及其对输电线路的影响。Mozer等［12］进行了连续3档导线、地线断线模拟试验，通过释放边档端部悬挂的重物来模拟导线、地线断线，得到了不同工况下导线、地线断线张力峰值及残余静态张力和钢管杆横担、塔身根部的应变，并确定了断线工况下结构动力响应系数。刘春城等［13］进行了模拟覆冰条件下五塔四线塔-线体系模型的断线冲击响应试验，测得了输电塔薄弱位置杆件的应变时程曲线，研究了塔-线体系在不同断线工况下杆塔的动力响应。

中国电力科学研究院［14］进行了±800 kV直线塔断线模拟试验，通过改变断线张力值模拟分裂导线断线，测试了不同断线工况下杆塔典型部位的位移和应变。东北电力设计院、中国电力科学研究院［15］完成了真型导线断线试验，试验中对铁塔杆件动应变、导线悬挂点位移进行了测量，铁塔杆件动应变峰值与稳定值之比在1.95 ～2.74 之间。

重覆冰是断线发生的主要原因之一，2008年电网冰灾后，新修订的设计规范中［16-17］将断线工况由无冰断线改为覆冰断线。以上有关断线的数值分析及试验研究中，大都未考虑覆冰影响。此外，断线响应还受导线阻尼、分裂数及子间隔棒等因素的影响，在进行导线断线动力分析时也应予以考虑。

随着特高压工程建设的不断推进，线路将不可避免地经过重覆冰区域。已经投运的±800 kV向家坝～上海直流输电线路经过重冰区，拟建的1 000 kV雅安～南京交流特高压线路将经过20 mm重冰区。

目前还没有针对重冰区特高压线路杆塔的断线响应及荷载取值进行分析研究。本文采用有限元分析和数值分析相结合的方法，通过建立重冰区特高压线路连续7档导线-绝缘子模型，考虑导线与地面接触、导线阻尼、分裂数和子间隔棒等因素的影响，研究不同因素对导线断线响应的影响规律，确定重冰区特高压线路悬垂型杆塔断线张力取值，研究结果对于保证重冰区特高压输电线路杆塔结构的安全性和可靠性具有重要意义。

1 分析模型

1.1 有限元模型

采用有限元软件ANSYS建立导线-绝缘子有限元模型，耐张段两端导线端点固接。悬垂绝缘子一般通过U型环或球头与杆塔横担连接，可绕顺线路和横线路方向转动，采用LINK8杆单元模拟绝缘子串;导线均采用LINK10杆(索)单元模拟。有限元模型中导线的单元长度可取为10 m。本次分析采用降温法施加导线的初始张力，即通过在导线索单元上施加等效温度来实现初始预张力。导线初始张力按照安装工况下线路段的代表档距［3］确定。

在进行断线分析之前，先进行自重作用下的导线找形分析。体系阻尼以Rayleigh阻尼［18］形式施加，断线采用杀死断线位置的导线单元来实现，被杀死单元的刚度在断线瞬间变为接近零的数值。

1.2 分析模型验证

中国电力科学研究院［19］通过构建四杆三线模型，进行了覆冰导线断线试验，第1档导线跨中位置发生断线。各档档距依次为95 m、100 m和95 m。导线选用输电线路工程常用导线型号JL/GIA 240/30，导线机械力学特性见表1，试验工况描述见表2。

表1 导线机械性能表Tab.1 Mechanical parameters of the conductors

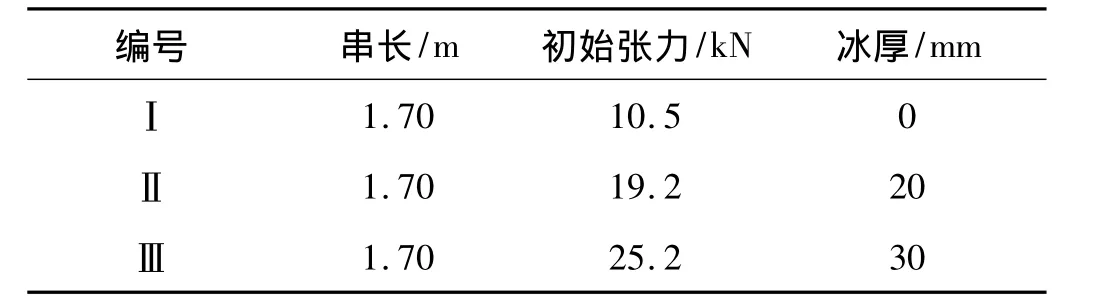
表2 试验工况编号及说明Tab.2 Numbers and illustration for the experimental cases

连续3档导线有限元模型如图1所示，分析中不考虑导线与地面接触的影响。各工况阻尼比根据试验识别结果取值，依次为0.011，0.015 和 0.036。通过进行断线瞬态分析，得到不同断线工况下第3档导线的残余静态张力及动态张力并与试验值进行比较，结果见表3。ANSYS瞬态分析计算值与试验值基本一致，最大误差约为7.5%。

图1 连续3档有限元模型Fig.1 FEA model of a three continuous span conductors

表3 断线张力对比Tab.3 Comparison on the tensions from broken conductors

2 断线响应分析

导线型号LGJ630/45，单根导线最大使用张力为56.50 kN，极限拉断力为141.26 kN。断线位置在第5档临近第4悬垂串处。左起前4档与后3档之间有15%高差;第5档档距为575 m，其余档档距均为500 m。代表档距为510.7 m，初始张力为23.40 kN。绝缘子串结构长度为11.7 m，绝缘子弹性模量取118 GPa，泊松比取 0.16。

影响因素分析中假定断线时无冰无风，建立连续7档有限元分析模型，计算不同工况下导线断线响应，研究导线与地面接触、导线阻尼、分裂数和子间隔棒等因素对导线断线响应的影响规律。

2.1 导线与地面接触

假定地面与导线弧垂最低点的垂直距离为50 m。地面材料:E=4 ×107Pa，ν=0.3，ρ=1 800 kg/m3。导线与 地 面 的 动 摩 擦 系 数 为 1.5［6］。地 面 采 用TARGE170单元模拟，断线档导线采用接触单元CONTA175模拟，接触单元不考虑初始化含穿透。考虑接触的有限元模型如图2所示，导线一阶和二阶阻尼比均取2%。

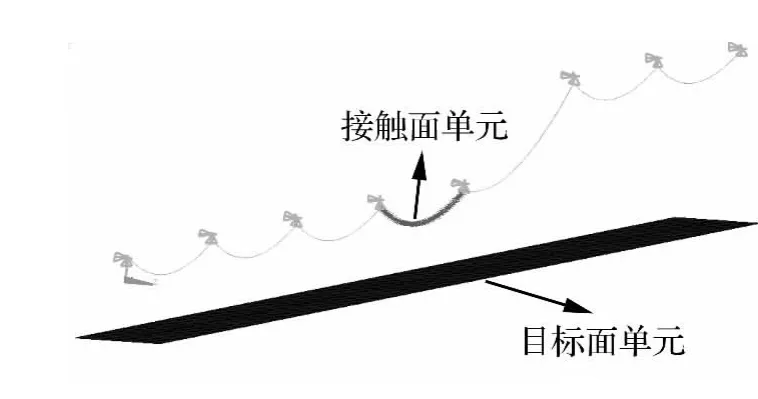
图2 有地面接触的有限元模型Fig.2 FEA model considering the conductor-ground effect

八分裂导线按照刚度、质量等效原则简化为单导线。采用瞬态分析方法计算得到断线点位移和各悬垂串端部承受的断线不平衡张力(以下简称“断线张力”)，最大断线张力发生在断线点附近的第4悬垂串处。

考虑地面接触前后，断线点位移和第4悬垂串处断线张力时程见图3。可以看出，无接触模型中，断线档导线沿竖向运动，断线后导线应变能和位置势能衰减，转化为动能;当向下运动达到某一位置时，动能达到最大值，之后导线开始向上反弹。有接触模型中，导线逐渐下降直至与地面接触，后发生反弹，反弹位移逐渐衰减。由于断线冲击效应的最大值发生在2 s～3 s之间，此时导线与地面尚未发生接触，因此采用两种模型计算得到的断线张力相差不大。

2.2 阻尼

计算条件同2.1节，断线点位于第5档导线临近第4绝缘子处，计算阻尼比取不同值时的断线张力和垂直荷载峰值，最大断线张力和垂直荷载分别发生在断线点附近的第4和第5悬垂串处。导线-悬垂串体系的前2阶自振频率为0.086 Hz和0.091 Hz。

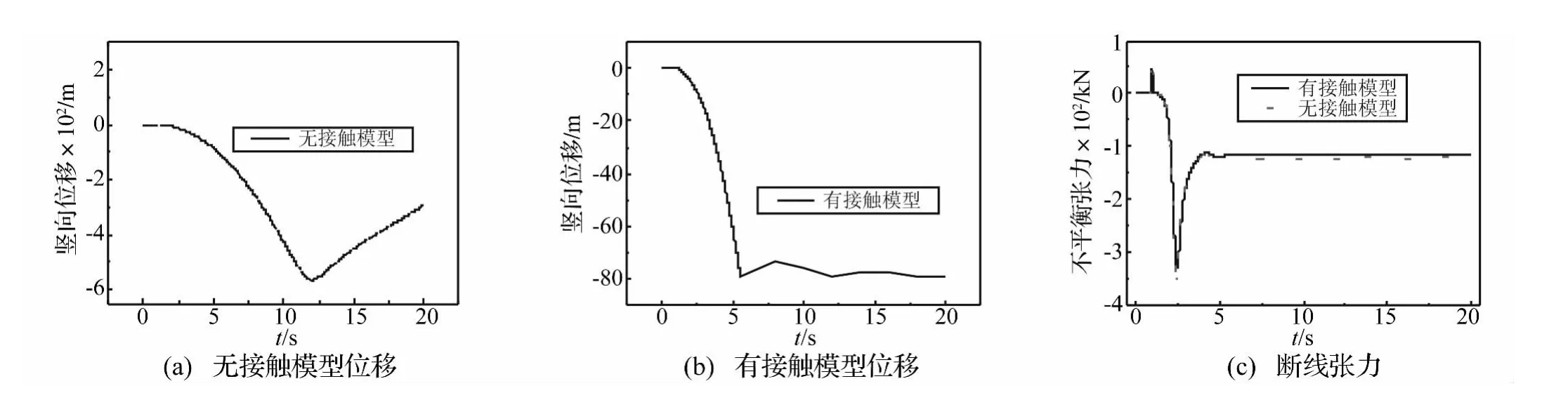
图3 断线响应时程对比Fig.3 Comparison on the time histories of the dynamic responses from broken conductors

表4 不同阻尼比断线响应Tab.4 Dynamic responses for different damping coefficients

根据模态分析得到的一阶频率和二阶频率，可以得到质量阻尼比α和刚度阻尼比β。一般来讲，α阻尼与质量有关，主要影响低阶振型;β阻尼与刚度有关，主要影响高阶振型。但对于非线性瞬态分析，导线刚度随张力变化而发生较大变化时，β阻尼会对断线响应产生较大影响。由表4可知，前二阶阻尼比分别为5%、10%和10%、20%时，β阻尼较大，断线张力、垂直荷载较小。

2.3 模型分裂数

建立连续7档八分裂导线-绝缘子模型，档距、高差、导线型号同2.1节。八分裂导线采用环形布置，外接圆直径 D为 1.0 m，子间隔棒和连接金具采用BEAM4梁单元模拟，八分裂-绝缘子有限元模型如图4 所示，各档间隔棒数依次为 8，8，8，8，9，8，8。

图4 八分裂导线有限元模型Fig.4 FEA model for eight bundles of conductors

分别采用八分裂模型和单导线等效模型进行断线动力分析，断线响应计算结果见表5和图5。可以看出，采用两种模型得到的断线张力随时间变化趋势相同，八分裂模型计算得到的断线张力和断线点位移略小于等效单导线模型计算值。

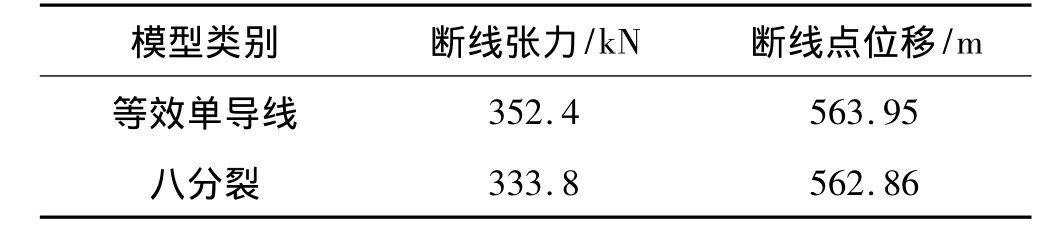
表5 不同分裂模型断线响应对比Tab.5 Comparison on the dynamic responses by models with different bundles

2.4 子间隔棒

分别建立无子间隔棒和有子间隔棒导线-绝缘子模型，计算条件同2.3节，分析不同根数子导线断裂时导线-绝缘子体系的动力响应。

2.4.1 无子间隔棒模型

采用无子间隔棒模型，分别计算断1～8根子导线时的断线张力、垂直荷载和未断子导线张力，计算结果见表6和图6。

表6 不同子导线数断线响应(无子间隔棒)Tab.6 Dynamic responses for different numbers of broken conductors(without spacer)

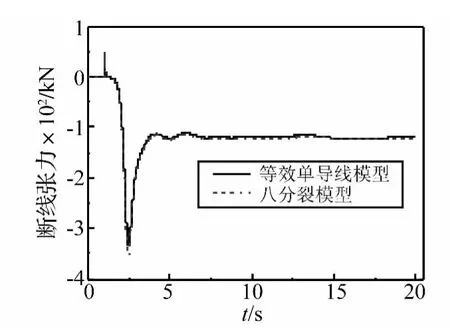
图5 不同分裂数模型断线张力对比Fig.5 Comparison on the time histories of the unbalanced tensions by models with different bundles

图6 无子间隔棒模型断线响应时程Fig.6 Time histories of the dynamic responses by models without spacers

由图6可以看出，不同根数子导线发生断裂时，断线响应随时间的变化趋势基本一致。随着断裂子导线根数的增加，断线张力、垂直荷载逐渐增大。断1～7根子导线时，剩余子导线可以承受部分断线张力;断8根子导线相当于整相断线，断线张力明显高出其他工况。子导线断线数达到5根以上时，未断子导线张力接近或超过导线最大使用张力;子导线断线数达到7根时，假定未断子导线张力超过导线计算拉断力也会发生断裂，相当于整相断线的情况。

2.4.2 有子间隔棒模型

采用有子间隔棒模型，分别计算断1、2、4、6和8根子导线时的断线张力，计算结果见表7。

对比表7和表6可知，断8根子导线时，由于子导线之间无限制作用，子间隔棒对断线张力的影响较小。对于断1～6根子导线的情况，由于未断裂子导线对断裂子导线的下降运动有限制作用，重力势能变化仅限于两个子间隔棒之间的导线，动能变化量较小，因而产生的断线张力非常小，与无子间隔棒模型有较大差异。鉴于目前规程出于安全考虑，有关断线荷载的计算并未考虑子间隔棒的影响，后面的断线荷载取值分析时采用无子间隔棒模型。

表7 不同子导线数断线响应(有子间隔棒)Tab.7 Dynamic responses for different numbers of broken conductors(with spacer)

3 悬垂型杆塔断线张力取值分析

3.1 静力分析

按照《重覆冰架空输电线路设计技术规程》［17］中规定的覆冰率，依据等线长法编制单导线断线张力计算程序［18］，计算20 mm～50 mm重冰区悬垂型杆塔导线断线张力及最大使用张力百分数。20 mm冰区采用导线型号为LGJ630/45;30 mm～50 mm冰区采用导线型号为ACSR-720/50，导线最大使用张力66.48 kN。

断线采用连续7档模型，无档距差和高差，断线发生在第1档或第7档，结合重冰区规程相关规定和以往线路实际运行经验，考虑整相(全部子导线)发生断线，20 mm(III冰区)、30 mm(IV 冰区)、40 mm(V 冰区)和50 mm(VI冰区)覆冰对应的单档使用档距分别为450 m、400 m、400 m和350 m。特高压线路覆冰率均按照一类线路取值，各个冰区对应的断线张力占最大使用张力百分数及与重冰区规程规定下限值对比见表8。

表8 悬垂型杆塔断线张力占最大使用张力百分数取值对比Tab.8 Comparison on the tension percentages of broken conductors for suspension towers

由表8可以看出，特高压线路20 mm、30 mm冰区断线张力计算略小于规程规定下限值;其余冰区均高于规程规定下限值，其中40 mm、50 mm冰区断线张力取值相差约10%。

3.2 动力分析

结合以往研究成果和规程相关规定，动力分析时假定第1档靠近悬垂串处的八分裂导线断4根子导线，计算不同冰厚时的断线张力Tbd和断线张力占最大使用张力百分数αbs。其余参数取值同静力计算。

由表9和表10可以看出，断4根子导线时，断线张力占最大使用张力百分数远小于规程规定值;随冰厚的增加，动力分析计算值与规程规定值的差值逐渐减小。考虑重冰区特高压输电线路的重要性和以往规范规定及其他电压等级重冰区输电线路运行经验，重冰区特高压输电线路悬垂型杆塔断线张力依照静力计算结果取值。

表9 悬垂型杆塔断线张力(20 mm、30 mm冰厚)Tab.9 Unbalanced tensions from broken conductors for suspension towers(20 mm and 30 mm ice)

表10 悬垂型杆塔断线张力(40 mm、50 mm冰厚)Tab.10 Unbalanced tensions from broken conductors for suspension towers(40 mm and 50 mm ice)

4 结论

(1)断线冲击响应的最大值一般发生在2 s～3 s之间，此时导线与地面尚未发生接触，因此考虑地面接触前后断线张力计算结果基本一致。

(2)对于子导线未全部断裂的情况，由于未断裂子导线对断裂子导线的下降运动有限制作用，重力势能变化仅限于两个子间隔棒之间的导线，动能变化量较小，因而产生的断线张力远小于无子间隔棒模型计算值。

(3)对于悬垂型杆塔，静力分析得到的20 mm、30 mm冰区断线张力值略小于规程规定下限值;其余冰区均高于规程规定下限值，其中40 mm、50 mm冰区断线张力取值相差约10%。

(4)对于悬垂型杆塔，动力分析时假定八分裂导线断4根子导线，断线张力占最大使用张力百分数小于规程规定值;随冰厚的增加，计算值与规程规定值的差值逐渐减小。

［1］廖宗高，陈海波，肖立群，等.特高压输电线路直线塔纵向不平衡张力取值的探讨［J］.电力建设，2006，27(2):1-3.LIAO Zong-gao，CHEN Hai-bo，XIAO Li-qun，et al.Investigation into longitudinal unbalanced tension value of UHV transmission suspension towers［J］.Electric Power Construction，2006，27(2):1-3.

［2］中国电力工程顾问集团公司.输电线路不平衡张力与断线张力取值分析报告［R］.北京，2006.

［3］东北电力设计院.电力工程高压送电线路设计手册［M］.北京:中国电力出版社，2002.

［4］李 黎，夏正春，江宜城，等.输电线断线振荡研究［J］.工程力学，2008，25(6):165-169.LI Li，XIA Zheng-chun，JIANG Yi-cheng，et al.Study on wire breaking-induced vibration of electric transmission line［J］.Engineering Mechanics，2008，25(6):165-169.

［5］夏正春，李 黎，梁政平，等.输电塔在线路断线作用下的动力响应［J］.振动与冲击，2007，26(11):45-49.XIA Zheng-chun，LI Li，LIANG Zheng-ping，et al.Dynamic response of transmission tower with ruptured wires［J］.Journal of Vibration and Shock，2007，26(11):45-49.

［6］沈国辉，默增禄，孙炳楠等.突然断线对输电塔线体系的冲击作用研究［J］.振动与冲击，2009，28(12):4-8.SHEN Guo-hui，MO Zeng-lu，SUN Bing-nan，et al.Research of impact effect on transmission line system due to sudden breakage of conductor［J］.Journal of Vibration and Shock，2009，28(12):4-8.

［7］Yang F L，Yang JB.Analysis on the dynamic responses of the broken conductors in transmission lines［J］.Applied Mechanics and Materials，2011，50-51:511-515.

［8］Siddiqui F M A，Fleming J F.Broken wire analysis of transmission line system ［J］.Computers and Structures，1984，18(6):1077-1085.

［9］Thomas M B，Peyrot A H.Dynamic response of ruptured conductors in transmission lines［J］.IEEE Transactions on Power Apparatus and Systems，1982，101:3022-3027.

［10］刘春城，初征宇，孙显鹤，等.大跨越高压输电线路覆冰断线的冲击动力学模型［J］.振动与冲击，2012，31(3):43-48.LIU Chun-cheng，CHU Zheng-yu，SUN Xian-he，et al.Impact dynamics model of long span high voltage transmission lines subjected to iced wire breakage［J］.Journal of Vibration and Shock，2012，31(3):43-48.

［11］ Peyrot A H，Kluge R O，Lee J W.Longitudinal loads from broken conductors and broken insulators and their effect on transmission lines［J］. IEEE Transactions on Power Apparatus and Systems，1980，99:222-231.

［12］ Mozer J D，Wood W A，Hribar J A.Broken wire tests on a model transmission line system ［J］.IEEE Transactions on Power Apparatus and Systems，1981，PAS-100(3):938-945.

［13］刘春城，毛绪坤，刘法栋，等.大跨越输电塔-线体系覆冰断线模型试验研究［J］.振动与冲击，2012，31(24):41-47.LIU Chun-cheng，MAO Xu-kun，LIU Fa-dong，et al.Model test for icing line disconnection on a long-span transmission tower-line system ［J］.Journal of Vibration and Shock，2012，31(24):41-47.

［14］中国电力科学研究院.±800 kV特高压直流断线试验分析报告［R］.北京，2007.

［15］东北电力设计院.67型Z1型单回路直线塔断线试验分析报告［R］.北京，1967.

［16］GB 50545-2010，110 kV～750 kV架空输电线路设计规范［S］.北京:中国计划出版社，2010.

［17］DL/T 5440-2009，重覆冰架空输电线路设计技术规程［S］.北京:中国电力出版社，2009.

［18］克拉夫 R，彭津 J，著，王光远 校.结构动力学［M］.北京:高等教育出版社，2006.

［19］中国电力科学研究院.重冰区特高压线路杆塔设计关键技术研究［R］.北京，2011.