一种改进的自适应格型陷波频率估计算法及其收敛性分析

沈廷鳌，涂亚庆，张海涛，杨辉跃

(后勤工程学院 信息工程系，重庆 401311)

频率估计是信号处理中的一项重要技术，在通信、声纳、振动控制、生物医学等方面均有着广泛的应用。主要的频率估计方法可分为参数模型法和非参数模型法［1－2］:两者均具有较高的频率分辨率，但参数模型法的性能受初始参数影响较大;非参数模型法存在计算量较大和难以实时实现的问题。

利用自适应陷波器进行频率估计，实际就是对其进行参数优化的问题。自适应陷波器可以根据被处理信号的特点，自动调节自身模型参数，以确定最优陷波频率，实现频率的实时测量与跟踪而倍受国内外研究者［3－5］的关注。其中，自适应格型陷波器由于结构算法简单、短时频率跟踪精度较高而得到了较广泛的应用［6－9］。然而陷波器均存在一个难题:即滤波器的非二次误差曲面含有局部最优值，当算法梯度达到一个局部最优值时，算法将固定参数值在局部最优值上而停止调整，从而丧失对信号频率变化的持续跟踪能力。

本文利用滤波增强信号与原始信号的相关性，设计一个频率跟踪质量评价因子，借鉴反馈控制的思想，根据频率跟踪质量实时监测并自动调整陷波参数，以实现持续稳定地跟踪信号频率的变化。据此原理，为推动自适应格型陷波器得到更为广泛的应用，本文提出了一种改进算法，以提高算法的收敛速度和持续跟踪精度，给出了具体的实现算法，并利用MATLAB仿真与原有算法进行了有关性能的比较分析。

1 自适应格型陷波器

自适应格型陷波器由全零点和全极点两个格型滤波器级联而成［6－8］。为了降低计算复杂度，徐科军等［9］把零点固定在单位圆上，通过调整一个参数就可实现自适应陷波。其实现方式如图1所示，传递函数为:

式中:k0为权系数，用于计算信号陷波频率，k0经过一段时间后会自适应收敛到－cosω;ω为被处理信号y(n)的归一化频率;ρ为去偏置参数，决定陷波器陷阱带宽。

y(n)－x(n)为去除噪声后的增强信号，具体的实现算法参见参考文献［9］。

图1 自适应格型陷波器的结构Fig.1 Structure of lattice-based adaptive notch filter

2 改进算法

2.1 问题分析

自适应陷波器的内部结构会导致非二次型误差曲面收敛至局部最优，从而使得陷波器不完全收敛［10－11］，当待估信号频率很低或很高时尤为明显。图2给出了自适应陷波器跟踪单正弦信号的误差曲面［12］。图2(a)收敛因子ρ≈1，收敛区域内误差陷入局部最优，梯度降为0，从而导致算法丧失自适应能力;图2(b)为正常跟踪信号频率的情况。

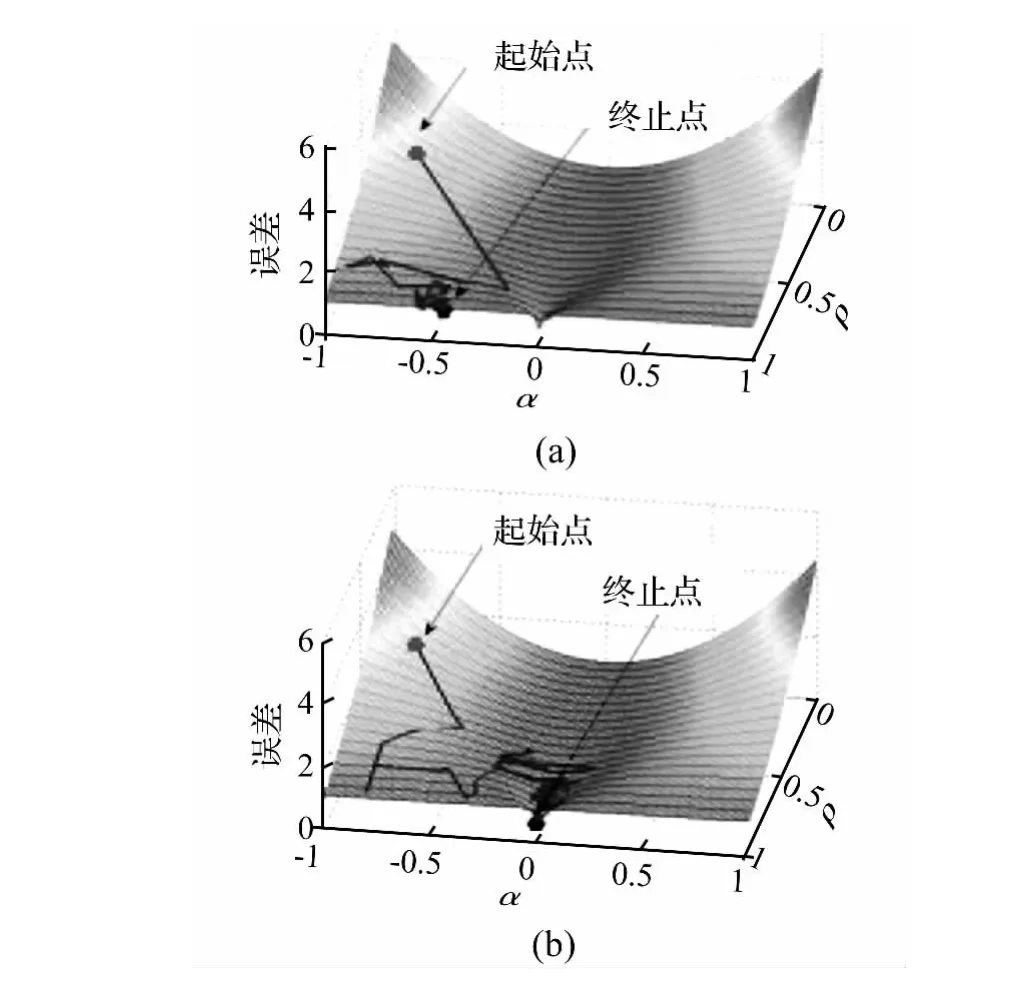
图2 错误跟踪(a)和正常跟踪(b)时陷波器的误差曲面Fig.2 Thefilter’s error surface in the case of(a)frequency miss-lock(b)correct frequency lock

在自适应调整过程中，随着收敛因子趋近于1，误差曲面将陷入局部最优，导致陷波器无法感知信号频率的变化，从而失去对信号频率变化的持续跟踪能力。

2.2 改进措施

当误差曲面陷入局部最优时，陷波器失去自适应能力，此时，可通过调整陷波器参数来增加陷波带宽的方法，让其重新恢复自适应能力。原理分析如下:

采用陷波器跟踪信号频率，在输入信号先验知识未知时，初始陷波带宽往往较大，以便能尽快捕捉到信号频率。随着陷波参数的自适应调整，收敛因子ρ趋近于1，陷波带宽趋近于0，误差曲面将陷入局部最优值而非全局最优值，陷波器可能锁定在一个错误频率上，此时，信号频率在陷波带宽之外，频率估计结果存在较大偏差。在这种情况下，增加陷波带宽可使陷波器能重新跟踪信号频率的变化，让其恢复自适应能力。此外，当陷波器锁定在正确频率时，增加陷波带宽也不会对频率估计精度有太大影响，因为此时正确频率的误差曲面确保了频率是朝着原来正确方向调整的。

因此，一旦收敛因子ρ趋近于1，可通过增加陷波带宽的方法，以确保陷波器不会锁定在一个错误频率上，进而确保陷波器的有效性。

2.3 评价因子

采用增加陷波带宽的方法，能重新恢复陷波器的自适应能力，可提高收敛速度，但同时也会增大信号频率估计的方差，因为在增加陷波带宽的同时会引入部分噪声。为兼顾收敛速度和估计精度，需要增加一个频率跟踪质量评价因子，用于实时监测并自动调整陷波参数。频率跟踪质量评价因子的设计过程及原理分析如下:

设输入信号为y(n)=c(n)+e(n)，c(n)为时变正弦信号，e(n)为零均值高斯白噪声，c^(n)为滤波增强信号。由图1和式(1)可推导出:

由式(2)可知，c^(n)不依赖y(n)的前期输入，与噪声e(n)无关。若陷波器正常工作，则滤波增强信号c^(n)≈c(n)与y(n)显著相关;否则 c^(t)≈e(n)与 y(t)不相关。

为检测陷波器是否有效跟踪信号基频，根据c^(n)和y(n)的相关性，设计一个频率跟踪质量评价因子h(n)，h(n)可由图3所示的0阶LMS算法在线计算得到。

图3 改进的自适应格型陷波器结构Fig.3 Structure of the improved adaptive lattice notch filter

LMS算法可由下式表示:

式中:μh是步长，收敛状态下，h是维纳－霍夫(Wiener-Hopf)方程［12］的解:

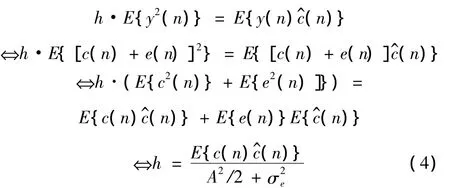
其中:

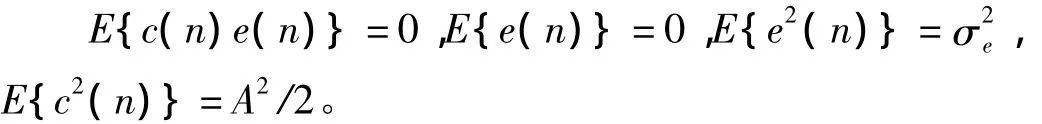
若陷波器正常跟踪信号基频，则c^(n)≈c(n)，h收敛为:

若陷波器锁定在错误频率上，则c^(n)与c(n)不相关，E{c(n)c^(n)}≈0，则 h≈0。因此，可通过检测h(n)的值来判断陷波器是否有效跟踪信号基频。若h(n)低于设定值Th，则说明陷波频率偏离信号基频，此时需对陷波器参数进行调整，以增加陷波带宽，进而使陷波器恢复自适应能力。

2.4 算法实现

根据上述分析，对自适应格型陷波频率估计算法进行改进，改进算法实现流程如图4所示。

具体实现算法如下:

Step1:初始化参数

k^0(0)，λ(0)，λr，λ∞，ρ(0)，ρr，ρ∞，Th，μh

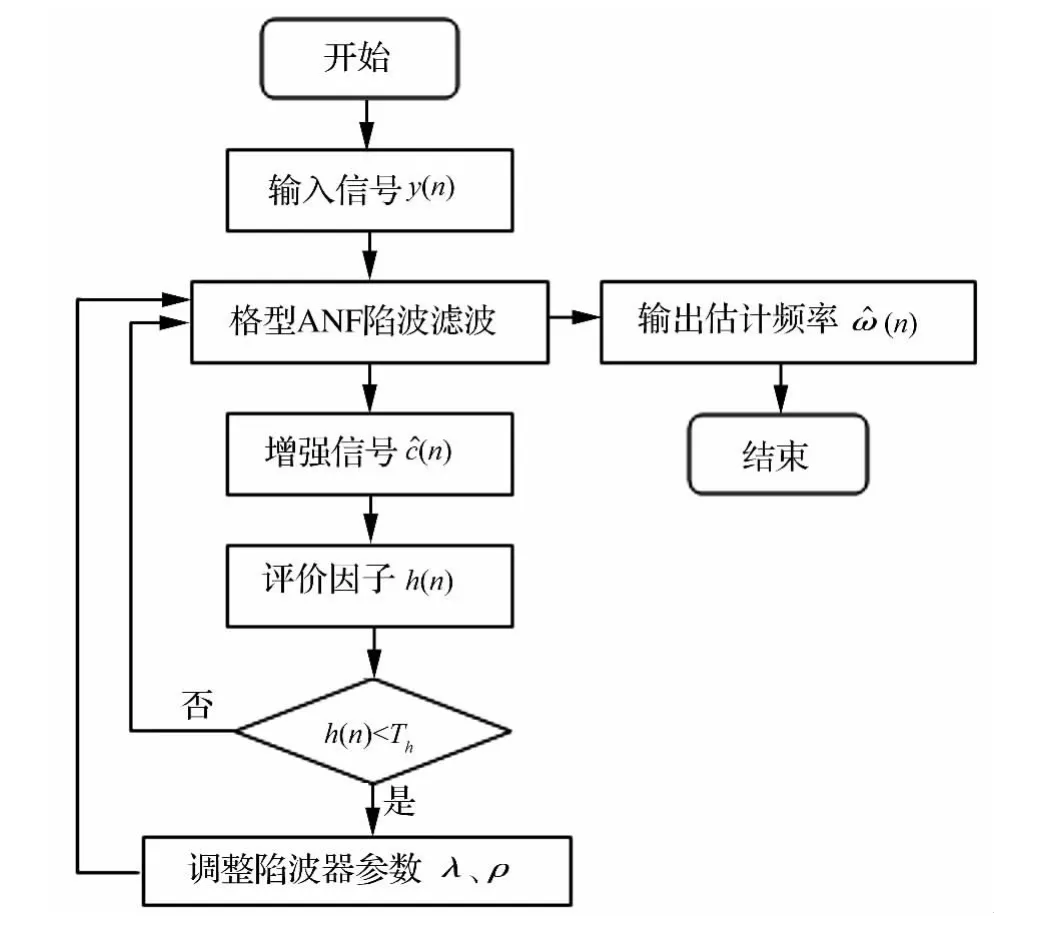
图4 改进算法流程图Fig.4 Flow chart of the improved algorithm

Step2:采用自适应格型陷波算法跟踪检测信号频率

Step3:根据频率跟踪质量实时监测并调整陷波参数

需要说明的是，如改进算法流程图及其具体实现算法所示:改进算法在原有算法的基础上，只是引进了一个频率跟踪质量评价因子，用于实时监测并自动调整陷波参数，本文仅是借鉴了反馈控制的思想，并没有增加算法的计算量。

3 仿真研究

设陷波器的输入信号由正弦信号和噪声信号组成，即

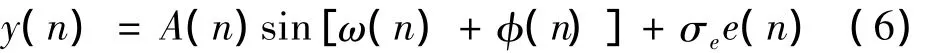
式中:幅值A(n)、归一化角频率ω(n)和相位φ(n)按照随机游动模型变化，时变信号模型及自适应格型陷波器相关参数值的选取参见参考文献［9］。

改进算法有关参数设定值为:

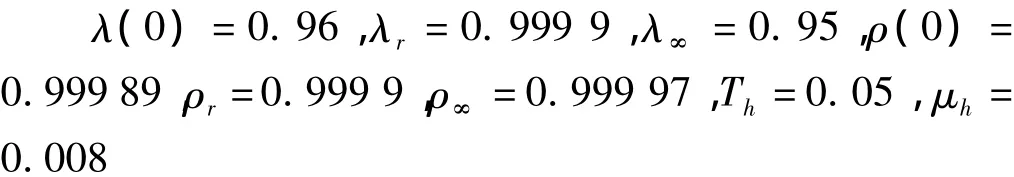
采用两种算法估计信号频率，图5～6为两次独立的仿真实验结果，从图中可以看出本文方法的频率跟踪曲线较好地与真实频率变化曲线吻合，与原有算法相比，本文方法的长时频率跟踪效果更好、精度更高。表1列出了两种算法真实频率均值均方误差均值MSE的比较，为去除收敛过程的影响，及MSE分别按下式计算:

天时——近年来电商和新能源的不断发展，催生很多老旧仓储中心升级改造和新兴仓储中心规划建设，其对于内部仓储设备的要求更加紧贴社会、科技发展，而中鼎在过去积累的定制化解决方案经验和核心设备的自主研发制造成为其独到的市场竞争优势；地利——民族品牌建设更加接地气，更加快速应对中国物流行业发展新需求，许多客户都赞许说：“中鼎仓储管理软件和自动化仓储设备，能够有效做到因需而变、快速反应”；人和——与诺力集团的合作，让中鼎的研发实力更加雄厚，产品线更加丰富，可为客户提供更加完善的仓储一体式解决方案。张总说：“当坐拥如此的“天时地利人和”，中鼎又岂能不收获成功呢？”

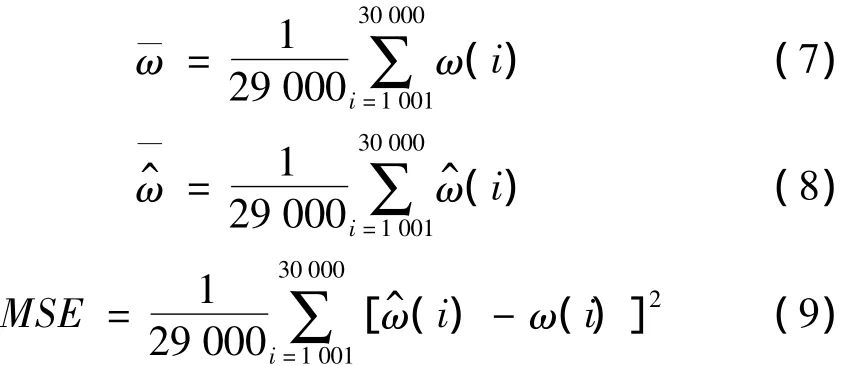
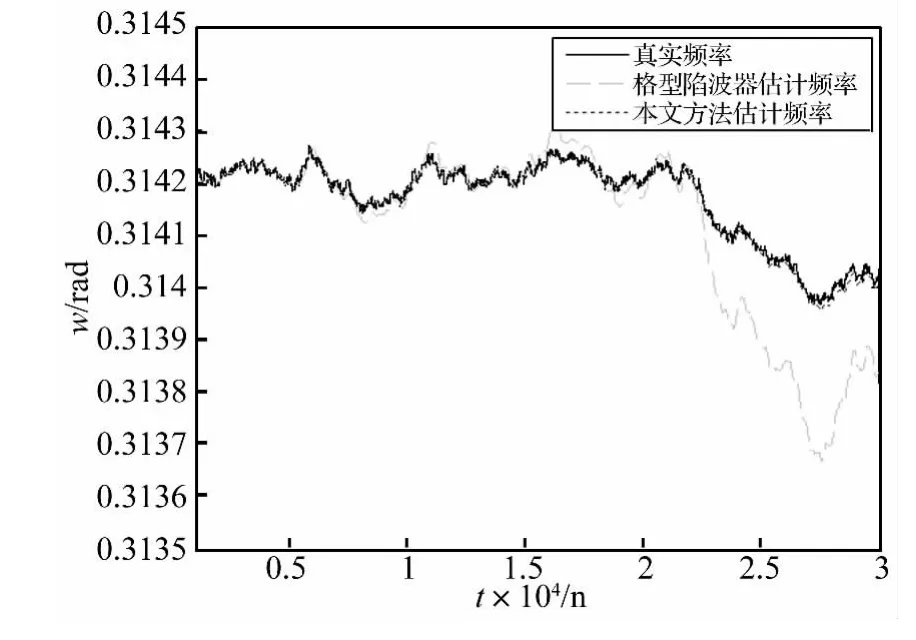
图5 真实频率与估计频率比较实验1Fig.5 Comparison experiment 1 between true frequency and estimated frequency

和MSE值的比较and MSE acquired by the two methods

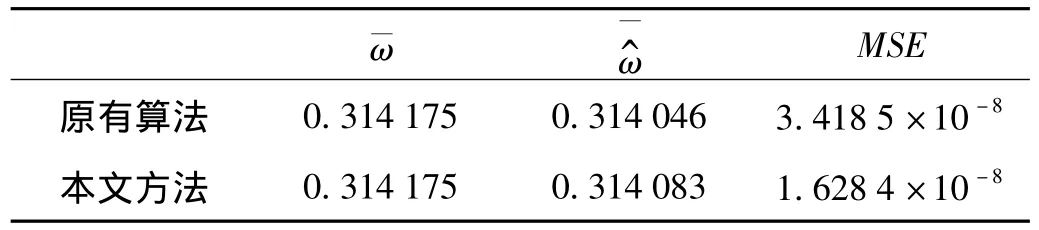
和MSE值的比较and MSE acquired by the two methods

MSE原有算法 0.314 175 0.314 046 3.418 5 ×10 ω— ω^—－8本文方法 0.314 175 0.314 083 1.628 4 ×10－8

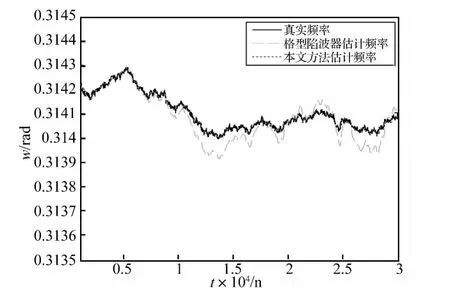
图6 真实频率与估计频率比较实验2Fig.6 Comparison experiment 2 between true frequency and estimated frequency

由表1可见，本文方法估计频率均值更接近真实频率均值，且均方误差均值更小，说明本文方法持续跟踪信号频率随机缓慢变化的精度和工作稳定性更好。

4 收敛性分析

通过分析陷波器原理可知，初始陷波带宽越宽，收敛速度越快。改进算法在原有算法的基础上增加了一个频率跟踪质量评价因子，用于实时监测和自动调整陷波参数。在陷波器跟踪信号频率的初始阶段，该评价因子能始终使改进算法保持较大的陷波带宽，以使改进算法能尽快捕捉到信号频率，因而可获得比原有算法更快的收敛特性。

从图5和图6可以看出，两种方法在前期估计信号频率的效果均较好，但无法从图形中对两种方法的收敛性进行比较分析。为了进一步考察两种方法的收敛特性，提出两种比较方法:

方法1:对EA值的偏差估计

首先定义如下函数:

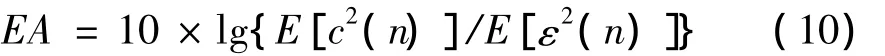
式(10)中，c(n)为正弦信号，ε(n)为输出信号。在理想状态下，陷波器将把正弦信号c(n)滤除，其输出只存在噪声信号e(n)，此时EA值即为信号的理想信噪比值。对EA值进行仿真分析，越先靠近并稳定在理想信噪比值的方法，其收敛速度越快，滤波效果越好。

方法2:对陷波滤波后的增强信号进行比较

对陷波滤波后的增强信号进行比较分析，增强信号越先达到稳定的，其收敛速度越快，滤波效果越好。采用陷波滤波后的增强信号来分析不同方法的收敛特性和滤波效果，是最直观有效的一种方法。

图7为原始信号经原有算法与经本文方法陷波滤波后得到的增强信号的比较。从图中可以看出，经原有算法陷波滤波后得到的增强信号在500点左右才达到稳定，而经本文方法陷波滤波后得到的增强信号在200点左右便达到稳定，其收敛时间更短，去噪效果更好，得到的增强信号受收敛过程的影响较小。

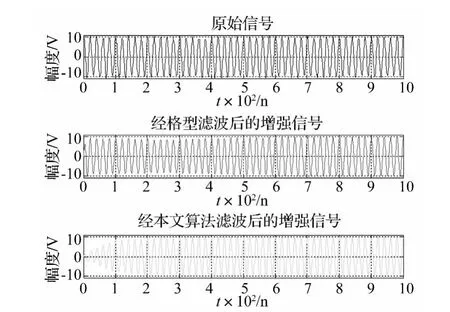
图7 经格型陷波器与本文方法陷波滤波后增强信号的比较Fig.7 Comparison of the enhanced signals by LANF and the presented method

5 结论

当收敛因子趋近于1时，自适应陷波器的内部结构将使得误差曲面陷入局部最优，从而失去对信号频率变化的持续跟踪能力。本文利用滤波增强信号与原始信号的相关性原理，设计一个频率跟踪评价因子，以实时监测并自动调整陷波参数，据此原理提出了一种改进的自适应格型陷波频率估计算法，并进行了仿真比较和性能分析。结果表明本文方法具有以下特点:

(1)改进算法的长时持续跟踪信号频率随机缓慢变化的精度和稳定性更好;

(2)改进算法在不增加计算量的前提下，收敛速度更快，去噪效果更好;

(3)本文方法的思想还可参考应用于其它类型的自适应陷波器。

［1］ Ignacio S，Carlos P，Jesus I.A comparative study of high －accuracy frequency estimation methods［J］.Mechanical Systems and Signal Processing，2000，14(5):819－834.

［2］张 磊，束立红，刘永光，等.基于级联自适应陷波器的正弦波频率估计［J］.信号处理，2006，22(3):387－389.ZHANG Lei，SHU Li-hong，LIU Yong-guang，et al.A method of sinusoidal frequency estimation based on cascaded adaptive notch filter［J］.Signal Processing，2006，22(3):387－389.

［3］张世平，赵永平，张绍卿，等.一种改进的自适应格型陷波算法及其收敛性分析［J］.电子学报，2004，32(2):338－341.ZHANG Shi-ping，ZHAO Yong-ping，ZHANG Shao-qing，et al.A modified adaptive algorithm of Lattice Notch Filter and its convergence analysis［J］.Acta Electronica Sinica，2004，32(2):338－341.

［4］储昭碧，张崇巍，冯小英.基于自适应陷波滤波器的频率和幅值估计［J］.自动化学报，2010，36(1):60－66.CHU Zhao-bi，ZHANChong-wei，FENGXiao-ying.Adaptive notch filter-based frequency and amplitude estimation ［J］.Acta Automatica Sinica，2010，36(1):60－66.

［5］涂亚庆，苏奋华，沈廷鳌，等.自适应陷波器的科氏流量计信号频率跟踪方法［J］.重庆大学学报，2011，34(10):147－152.TU Ya-qing，SU Fen-hua，SHEN Ting-ao，et al.Frequency tracking method and simulation for Coriolis Mass Flowmeter based on new adaptive notch filter［J］.Journal of Chongqing University，2011，34(10):147－152.

［6］ Regalia P.An improved lattice－based adaptive IIR notch filter［J］.IEEE Trans.Signal Processing，1991，39(9):2124－2128.

［7］ Cho N I，Lee S U.Tracking analysis of an adaptive lattice notch filter［J］.IEEE Trans.Circuits and Systems，1995，42(5):186－195.

［8］潘欣裕，赵鹤鸣，陈雪勤.修正自适应格型陷波器及其应用［J］.声学技术，2007，26(6):1254－1258.PAN Xin-yu，ZHAOHe-ming，CHEN Xue-qin.An improved adaptive lattice notch filter and its application［J］.Technical Acoustics，2007，26(6):1254 －1258.

［9］徐科军，倪 伟，陈智渊.基于时变信号模型和格型陷波器的科氏流量计信号处理方法［J］.仪器仪表学报，2006，27(6):596－601.XU Ke-jun，NI Wei，CHEN Zhi-yuan.A signal processing method for Coriolis mass flowmeter based on time－varying signal model and lattice notch filter［J］.Chinese Journal of Scientific Instrument，2006，27(2):596 －601.

［10］ Shynk J.Adaptive IIR filtering［J］.IEEE ASSP Magazine，1989，4:5－21.

［11］Ta M，Thai H，DeBrunner V.Adaptive tracking in the timefrequency plane and its application in causal real-time speech analysis［C］.ICASSP 2009:3233 －3236.

［12］Ta M，Thai H，DeBrunner V.Stochastic search methods to improve the convergence of adaptive notch filter［C］.IEEE 13th DSP workshop，2009:78－83.