轧机水平振动侧向液压振动抑制器抑振效果仿真研究
闫晓强,杨喜恩,吴先峰
(北京科技大学 机械工程学院,北京 100083)
连轧机振动是世界范围内普遍存在的问题。通过对某热连轧机的振动信号测试,发现当轧机在轧制过程中发生严重振动时表现为辊系水平振动大于垂直振动的现象。当适当改变辊系轴承座侧向液压缸压力时能够有效抑制轧机振动。因此可以推断:当侧向液压压力的振动与辊系水平主要振动频率相等且相位相反时,可能获得更好的抑振效果。
为了回答上述问题,利用MATLAB进行了抑振效果仿真研究。
1 液压振动抑制器模型建立
液压振动抑制器由压力给定、PI调节器、伺服放大器、伺服阀、液压缸、位移传感器和振动抑制器构成如图1所示。当辊系水平振动时,侧向液压缸也跟随振动,此时液压缸内的位移传感器输出振动信号,将此振动信号送到振动抑制器,振动抑制器接收到液压缸的振动信号经过特殊处理和变换后输出一个振荡信号送到伺服放大器的反馈输入端来控制伺服阀动作,使进入液压缸的油产生振荡,其频率和幅值与原振动大小相等而相位相反,从而抑制液压缸的振动,即抑制了辊系的水平振动。
为了对液压振动抑制器进行研究,需要建立系统的各个单元的模型和整体模型。其中侧向压力给定设为:P=6×102sin2πft kN,各单元的传递函数如图2。

图1 液压振动抑制器原理图Fig.1 Schematic diagram of hydraulic vibration suppression system
(1)信号调节器
本系统采用PI调节器,其传递函数可表示为:

式中:Kp为比例放大系数;Kis为积分时间常数。
(2)伺服放大器
电液伺服阀是电流控制型元件,为一个比例环节,其比例系数为:

式中:Ka为伺服放大器增益;I(s)为放大器输出电流;U(s)为输入的电压信号。
(3)电液伺服阀
电液伺服阀可简化为二阶振荡环节[1-2]:

式中:ksv为电液伺服阀流量增益,m3/s·A;ωv为电液伺服阀的固有频率,rad/s;ξv为伺服阀的阻尼系数,取值为 0.6;
s为拉普拉斯算子。
依据伺服阀资料,当ΔU=20×102kPa,Δi=20 mA时,空载流量:Q0(s)=90 L/min
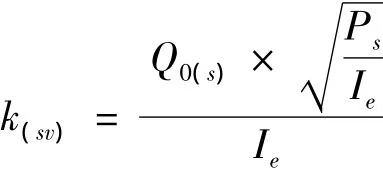
式中:Ps为伺服阀入口供油压力;Ie为额定电流。
(4)轧机横向负载
为便于分析,将轧机辊系-负载系统简化为两自由度弹簧-质量系统,用2个自由度的模型来分析,其传递函数为[3-4]:
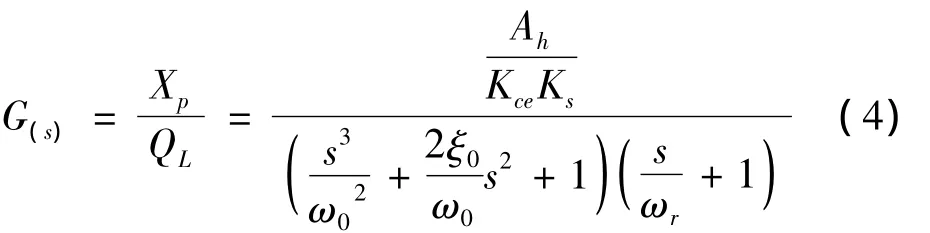
式中:Ah为油缸无杆腔的有效面积;Kce为总流量压力系数;Ks为轧机等效负载刚度;ω0为二阶环节固有频率;ωr为惯性环节转折频率;ξ0为振荡环节阻尼比。各个参数的确定如下:(a)总的流量压力系数

式中:Ci为油缸泄漏系数;ω为伺服阀阀口梯度;d为伺服阀阀芯直径,ω=πd;C为伺服阀阀套与阀芯间隙;μ为液压油的绝对粘度,μ=υ·ρ,v和ρ为40℃时液压油的运动粘度和密度。
(b)轧机的等效负载刚度

式中:M为负载质量;W为移动质量。
(c)惯性环节转角频率

(d)二阶振荡环节无阻尼自振频率

式中:βt为系统阻尼系数;Mt为移动质量。
(5)位移传感器
位移传感器的响应频率远高于液压缸的固有频率,其传递函数可视为比例环节:
Gf(s)=Kfs
式中:Kf为位移反馈系数。
(6)振动抑制器
振动抑制器将液压缸的振动信号经过处理和变换输出一个振荡信号送到伺服放大器的反馈输入端来控制伺服阀动作,使进入液压缸的油产生振荡,其传递函数可视为一阶环节[5]:

2 液压振动抑制器仿真研究
轧机技术参数为:轧机支承辊φ1 500×1 800 mm、工作辊φ750×2 000 mm。液压系统参数为:缸径φ480 mm、杆径φ400 mm、压力16 MPa、行程25 mm,主要参数如表1所示。根据系统的传递函数,利用Simulink得到系统仿真模型如图2所示。

表1 仿真主要参数一览表Tab.1 Simulation parameters list
当轧机辊系发生振动时,侧向液压缸也振动,但相位与辊系水平振动相反,使辊系振动减弱。
液压振动抑制器接收液压缸的振动信号,经过处理和变换输出一个振荡信号传送到伺服放大器的反馈输入端来控制伺服阀动作,使进入液压缸的油产生振荡,在理想状态下其频率和幅值与原振动大小相等而相位相反。为了观察反馈信号不同相位差下系统的响应曲线,设定7种相位的振动幅值变化情况如图3所示。

图2 轧机液压振动抑制器控制系统仿真模型Fig.2 Rolling mill hydraulic vibration suppressor control system simulation model

图3 不同相位差下系统的响应曲线Fig.3 Effect of the phase difference of the response curves of the system

表2 振幅减小率与相位差关系Tab.2 Relationship between of the amplitude reduce and phase difference
为了清晰起见,将液压油缸的振动相位与辊系水平振动相位差大小与抑振效果制成表2和图4所示。
由图4可以明显看出:随着液压缸振动与辊系水平振动的相位差增大,振动幅值降低百分比增加,当反向时抑振效果最好,从而抑制了轧机辊系的水平振动。
3 结论
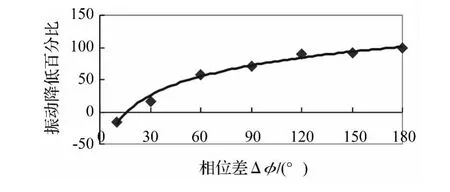
图4 振动幅值随相位差变化减小情况Fig.4 Relationship between of vibrationamplitude and phase difference
建立了液压振动抑制器的仿真模型,利用MATLAB进行了动态特性仿真研究,获得了良好的振动抑制效果,证明了该种抑振方法是可行的。
[1]王占林.液压伺服控制[M].北京:北京航空学院出版社,1987:44-50.
[2]王春行.液压控制系统[M].北京:机械工业出版社,2004:78-80.
[3]刘建昌,王贞祥,王立平,等.AGC系统控制模型与结构的研究[J].钢铁,1994,29(4):35 -39.LIU Jian-chang,WANG Zhen-xiang,WANG Li-ping,et al.AGC system control model and structure study[J].Iron and Steel,1994,29(4):35 -39.
[4]居兴华,赵厚信,杨晓臻.宝钢2050热轧板厚度控制系统的研究[J].钢铁,2000(l):60-73.JU Xing-hua,ZHAO Hou-xin,YANG Xiao-zhen.Baosteel 2050 hot strip rolling thickness control system[J].Iron and Steel,2000(1):60 -73.
[5]严金坤.液压动力控制[M].上海:上海交通大学出版社,1986.
[6]邹家祥,徐乐江.冷连轧机系统振动控制[M].北京:冶金工业出版社,1998.
[7]黄忠霖.控制系统Matlab计算及仿真[M].北京:国防工业出版社,2001.
[8]徐 听,李 涛,伯晓晨.Matlab工具箱应用指南一控制工具篇[M].北京:电子工业出版社,2000.
[9]侯东晓,刘 彬,时培明,等.两自由度轧机非线性扭振系统的振动特性及失稳研究[J].振动与冲击,2012,31(3):32-36.HOU Dong-xiao,LIU Bin,SHI Pei-ming,et al.Vibration characteristic of 2 DOF nonlinear torsional vibration system of rolling mill and its conditions of instability[J].Journal of Vibration and Shock,2012,31(3):32 -36.
[11] Yan X Q,Vibration control in thin slab hot strip mills[J].Ironmaking & Steelmaking,2011,38(4):309 -313.
[12]闫晓强,史 灿,曹 曦,等.CSP轧机扭振与垂振耦合研究[J].振动、测试与诊断,2008,28(4):377-383.YAN Xiao-qiang,SHI Can,CAO Xi,et al.CSP rolling mill coupled research of torsional vibration and vertical vibration[J].Vibration,Test and Diagnosis,2008,28(4):377-383.

