平稳地震动过程的随机函数-谱表示模拟
刘章军,方 兴
谱表示方法这一概念最早可追溯到Rice[1]、Goto等[2]以及 Borgman[3],他们应用谐波叠加法对一维随机过程进行了模拟。然而,Shinozuka等[4-5]正式提出了用谱表示方法模拟随机过程的一般原理,并用于模拟多维、多变量以及非平稳随机过程。在随后的40年中,诸多学者在这方面做了大量的研究工作,同时在工程领域也获得了广泛的应用。Shinozuka等[6]和Deodatis等[7]分别给出了单变量、一维随机过程以及多维高斯随机场的谱表示法的理论背景。Deodatis[8]模拟了各态历经的多变量平稳随机过程。Spanos等[9]对谱表示法所生成样本函数的性质、计算效率以及通用性等方面进行了讨论。总体而言,谱表示方法算法简单,理论完善,模拟结果较为可靠,但其计算工作量较大,特别地,对于工程实际问题,往往需要高达数百上千个随机变量才能保证所需的精度,从而极大地增加了问题的分析难度。为了有效地减少谱表示方法中随机变量的数量,陈建兵等[10]提出了随机过程的随机谐和函数表达方式,采用少量的项数(10个随机谐和分量),即可获得精确的目标功率谱密度函数,陈建兵等[11]进一步对谱表示方法的频率选点进行了优化。
本文在平稳随机过程的谱表示基础上,采用随机函数的思想,将谱表达式中的标准正交随机变量表示为基本随机变量的正交函数形式,从而实现了用1~2个基本随机变量即可描述原随机过程的概率特性,而且可以直接由功率谱密度函数生成具有给定概率的非高斯平稳过程和高斯平稳过程的样本函数。与文献[10]和文献[11]相比,本文方法所需随机变量的数量更少(仅需1~2个基本随机变量),这将为复杂工程结构的随机动力反应和动力可靠度的精细化分析提供重要基础。
1 平稳随机过程的谱表示
对于任意一个一维、单变量、零均值、双边功率谱密度函数为SX(ω)的实平稳随机过程X(t),存在两个相互正交的实过程u(ω)和v(ω),它们的增量d u(ω)和 d v(ω)相互正交,使下式成立[6]:

过程u(ω)和 v(ω)的增量 d u(ω)与 d v(ω)满足如下的条件:

对式(1)进行离散,可得:
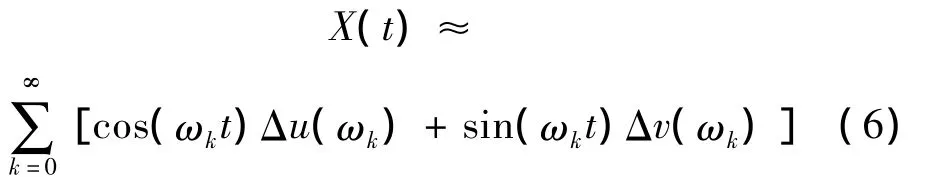
式中ωk=kΔω,且Δω要足够小,使得式(6)可以替代式(1)。
若增量 Δu(ωk)和 Δv(ωk)定义为[6]:

其中{Xk,Yk}为一组标准的正交随机变量,即:

式中δij为Kronecker-delta符号。容易证明,式(7)~式(9)所定义的增量Δu(ωk)和Δv(ωk)能满足式(2)~式(5)的条件。
于是,将式(7)和式(8)代入式(6)中,并取有限项作为对原随机过程的近似表达,则实平稳随机过程模拟的第一类谱表示[6]:

当随机过程的功率谱密度函数SX(ω0)=SX(0)=0时,可将式(10)改写为:

若进一步假定{Xk,Yk}(k=1,2,…,N)为相互独立的标准高斯随机变量,则式(11)所表达的平稳随机过程为高斯过程。
此时,平稳随机过程的均方相对误差:

式中截断频率ωu=NΔω。一般而言,εX(N)≪1,对于地震动加速度过程,其值不宜超过0.05。
2 标准正交随机变量的随机函数表达
在上述实平稳随机过程模拟的第一类谱表示(即式(11))中,{Xk,Yk}(k=1,2,…,N)为一组标准正交随机变量,它们满足条件式(9)。下面来构造标准正交随机变量{Xk,Yk}的随机函数形式。
首先,利用随机函数的思想[12],即假设任意的两组标准正交随机变量(n=1,2,…,N)分别是两个相互独立的基本随机变量(随机向量)Θ1和Θ2的函数,即分别是随机函数 gj(Θ1)和 hj(Θ2)。于是,式(9)可改写为:

其中:pΘ1(θ1)和 pΘ2(θ2)分别是 Θ1和 Θ2的概率密度函数。
2.1 非高斯随机变量的随机函数构造
容易验证,下列4组随机函数形式均能满足式(13)~式(17):
下面,以第4类随机函数的构造形式来加以证明。事实上,有:

2.2 高斯随机变量的随机函数构造
为了构造一组相互独立的标准高斯随机变量,首先,构造一组标准正交随机变量 ξn(n=1,2,…,N),若假定基本随机变量Θ在区间[-π,π]或[0,2π]上服从均匀分布,则可构造如下常用的三角正交函数:ξn=fn(Θ)=sin(nΘ + α),n=1,2,…,N (18)其中α为一确定性常数,通常可取α=0或α=π/4或α=π/2,此时 fn(x) =sin(nx)或 cas(nx)或cos(nx)。显然,ξn(n=1,2,…,N)是一组标准的正交随机变量。
在式(18)中,进一步推导可知,ξn(n=1,2,…,N)具有相同的概率分布函数[13]:

由此可见,ξn(n=1,2,…,N)是服从同一分布的标准正交随机向量。
为了获得一组具有高斯分布的标准正交随机变量ηn(n=1,2,…,N),可采用等概率的反变换方法[14]:

其中Φ-1为Φ的反函数。将式(18)、式(19)代入式(21)中,得到

于是,即可获得一组具有高斯分布的标准正交随机变量ηn(n=1,2,…,N)。根据随机变量的正交性(零均值情况)与独立性等价可知,ηn(n=1,2,…,N)为一组相互独立的标准高斯随机变量。
为此,以上述第1组和第2组的随机函数形式,即可构造相应的两组相互独立的标准高斯随机变量:

最后,按Matlab程序自带的rand('state',0),randperm(N)将。从而,所需的相互独立的标准高斯随机变量{Xk,Yk}(k=1,2,…,N)就能被唯一地确定。
3 平稳地震动过程的实例分析
3.1 地震动过程的基本信息
考虑平稳地震动加速度过程,其功率谱密度函数采用胡聿贤模型(单边谱)[15]:

式中:ωg和ζg分别为场地土的卓越圆频率和阻尼比,ωc为低频截止频率,其参数取值如表1所示。S0为基岩地震动加速度白噪声功率谱密度,它反映地震动的强弱程度,也简称为谱强度因子。

表1 功率谱模型的参数取值[16]Tab.1 The values of parameters in the power spectrum model
根据随机振动理论,谱强度因子S0可按下式计算:


对于不同的场地类别,参数a—max、f、ωe及S0的取值如表2所示。

表2 不同场地的谱强度因子取值Tab.2 Values of the spectral intensity factor for different site types
表2中地面加速度最大值的均值a—max是采用我国《建筑抗震设计规范》(GB 50011-2010)中给出的时程分析法所用地震加速度时程曲线的最大值。
3.2 分析与验证
为检验第一类谱表示-随机函数方法的有效性,以上述平稳地震动加速度过程为例,其中地震动参数的取值 ωg=15.71 rad/s,ζg=0.72,ωc=2.108 rad/s,S0=107 cm2/s3。在平稳地震动过程模拟的谱表示中,其参数取值 ωu=35 Hz=219.911 5 rad/s,Δω =0.122 17 rad/s,N=1 800,εX(N)=4.618%。为了获得地震动加速度过程的样本时程曲线,首先需要将基本随机变量离散化,表3给出了1个和2个基本随机变量的离散公式及离散点数s。然后根据标准正交随机变量的随机函数形式(这里以第1组随机函数和第2组随机函数为例),获得标准正交随机变量的离散点集及相应的赋得概率。最后,将标准正交随机变量的离散点代入平稳地震动过程的谱表达式(11)中,即可生成样本时程曲线。在地震动加速度过程的样本生成中,时间间隔Δt=0.01 s满足 Δt≤π/ωu的条件,图 1 给出了典型的平稳地震动加速度过程的样本时程曲线。

表3 基本随机变量的离散点集Tab.3 The discrete point set of basic random variables
图2和图3分别给出了以第1组和第2组随机函数表达的非高斯平稳过程的二阶数值统计量,其中图(a)为样本总体均值与目标均值函数的比较,图(b)为样本总体功率谱密度与目标功率谱密度函数的比较,从总体上看,它们之间的符合程度比较好。
图4和图5分别给出了以第1组和第2组随机函数表达的高斯平稳过程的二阶数值统计量,其中图(a)为样本总体均值与目标均值函数的比较,图(b)为样本总体功率谱密度与目标功率谱密度函数的比较。与图2和图3相比,高斯平稳过程的二阶数值统计量与目标统计量的符合程度要比非高斯平稳过程的符合程度略差一点,这可能是随机变量的高斯化变换过程中的高度非线性所致。

图1 平稳地震动加速度过程的样本时程曲线Fig.1 Sample functions of stationary ground motion acceleration processes

图2 以第1组随机函数表达的非高斯平稳过程(1个基本随机变量,1006个离散点)Fig.2 Expressed non-Gaussian stationary process using random functions in the first group(a basic random variable,1 006 discrete points)

图3 以第2组随机函数表达的非高斯平稳过程(2个基本随机变量,987个离散点)Fig.3 Expressed non-Gaussian stationary process using random functions in the second group(two basic random variable,987 discrete points)

图4 以第1组随机函数表达的高斯平稳过程(1个基本随机变量,1 006个离散点)Fig.4 ExpressedGaussian stationary process using random functions in the first group(a basic random variable,1 006 discrete points)

图5 以第2组随机函数表达的高斯平稳过程(2个基本随机变量,987个离散点)Fig.5 Expressed Gaussian stationary process using random functions in the second group(two basic random variable,987 discrete points)
4 结论
工程随机过程的合理描述与建模,是结构随机动力学分析的重要基础。经典的谱表示方法往往需要高达数百上千个随机变量才能保证所需的精度,从而极大地增加了分析的难度和计算工作量。本文提出的随机函数-谱表示方法,将谱表达式中的标准正交随机变量表示为1~2个基本随机变量的正交函数形式,从而实现了用基本随机变量描述原随机过程的概率特性。研究表明,用随机三角函数表达标准正交随机变量,不仅能构造正交的非高斯随机变量,也能构造相互独立的高斯随机变量,从而可方便地由功率谱密度函数生成具有给定概率的非高斯平稳过程和高斯平稳过程的样本函数。最后,以平稳地震动加速度过程的功率谱密度函数为例,验证了本文方法的有效性和优越性。
[1] Rice S O.Mathematical analysis of random noise[J].Bell System Technical Journal,1944,23(3):282 - 332,and 1945,24(1):46 - 156.Reprinted in:N.Wax(Ed.),Selected Papers on Noise and Stochastic Process,Dover Publications,Inc.,New York,1954:133 -294.
[2]Goto H,Toki K.Structural response to nonstationary random excitation[A].Proc.4th WCEE,Santiago,Chile,1969.
[3]Borgman L E.Ocean wave simulation for engineering design[J].Journal of the Waterways and Harbors Division,ASCE,1969,95(4):557-583.
[4]Shinozuka M.Simulation of multivariate and multidimensional random processes[J].Journal of the Acoustical Society of America,1971,49(1):357-368.
[5] Shinozuka M,Jan C M.Digital simulation of random processes and its applications[J].Journal of Sound and Vibration,1972,25(1):111-128.
[6]Shinozuka M,Deodatis G.Simulation of stochastic processes by spectral representation[J].Applied Mechanics Review,1991,44(4):191-204.
[7]Shinozuka M,Deodatis G.Simulation of multi-dimensional Gaussian stochastic fields by spectral representation [J].Applied Mechanics Review,1996,49(1):29-53.
[8] Deodatis G.Simulation of ergodic multivariate stochastic processes[J].Journal of Engineering Mechanics,1996,122(8):778-787.
[9] Spanos P D,Zeldin B.A.Monte Carlo treatment of random fields:A broad perspective[J].Applied Mechanics Review,1998,51(3):219-237.
[10]陈建兵,李 杰.随机过程的随机谐和函数表达[J].力学学报,2011,43(3):505 -513.CHEN Jian-bing,LI Jie.Stochastic harmonic function and spectral representations[J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(3):505 -513.
[11]陈建兵,李 杰.谱表达方法的频率取点优选[J].振动工程学报,2011,24(1):89-95.CHEN Jian-bing,LI Jie.Optimal selection of frequencies in the spectral representation method[J].Journal of Vibration Engineering,2011,24(1):89-95.
[12]李 杰.随机结构系统——分析与建模[M].北京:科学出版社,1996.
[13]汤保新,刘 平.随机结构的单源随机向量表达[J].扬州大学学报(自然科学版),2011,14(4):64 -68.TANG Bao-xin,LIU Ping.Expression of stochastic structures with monophyletic random vector[J].Journal of Yangzhou University(Natural Science Edition),2011,14(4):64-68.
[14]刘章军,陈建兵.结构动力学[M].北京:中国水利水电出版社,2012.
[15]胡聿贤,周锡元.弹性体系在平稳和平稳化地面运动下的反应[A].地震工程研究报告集第一集[C].北京:科学出版社,1962:33-50.
[16]薛素铎,王雪生,曹 资.基于新抗震规范的地震动随机模型参数研究[J].土木工程学报,2003,36(5):5-10.XUE Su-duo WANG Xue-sheng,CAO Zi.Parameters study on seismic random model based on the new seismic code[J].China Civil Engineering Journal,2003,36(5):5 -10.
[17] Li J,Chen J B.The number theoretical method in response analysis of nonlinear stochastic structures[J].Computational Mechanics,2007,39(6):693 -708.

