旅游供应链中供货商与投机商的收益协调研究

□周垂日 吴 钰 [中国科学技术大学 合肥 230026]

引言

供应链管理是目前比较流行的管理模式，旅游供应链主要研究的是旅游经济活动中各参与方之间的相互关系，早在2004年和2005年，Alford[1]与Tapper[2]就给出了旅游供应链的描述性论述。我们研究旅游供应链的目的，是在于降低成本费用，从而实现各方合作利益的最大化，那么，协调就成为实现这些目标的基础和必要前提。

在旅游供应链的研究中，大部分讨论的是供货商、代理商以及策略型消费者的关系[3]，尤其对于销售有时间限制的商品，企业可以通过动态定价使得销售收入最大，这类问题通常被称为收益管理问题[4]。然而在市场中，还存在这样一类人群，他们不以消费为目的购买产品，他们购买产品的目的纯粹是为了再次转卖，从而获得利润，我们称这类人为投机商[5]。一般情况下，当游客对价格变化不具有异质性，即游客都是对价格不敏感的，他们不会主动寻找价格较低的商品，此时供货商是不需要考虑与投机商合作的。但是，当市场中存在价格敏感型游客，如果供货商提供的商品价格不具有竞争性时，这些游客或许会选择从价格较低的其他地方购买商品（如投机商处），或许会退出市场，终止购买行为。在这种情况下，作为供货商的一方，就具有了与投机商合作的基础，而合作的最终目的，是使得双方都能从合作中受益。

在早前旅游供应链文献的研究中，Guo与Yang等就使用了博弈论的方法，分析了旅游供应链中的企业采取的战略问题[6,7]。在这篇文章中，我们考虑的是投机商与供货商进行的是合作博弈的情况[8]，即供应链中的双方能够以集体利益最大化为目标而采取合作的策略。为了使得模型容易被理解，我们以出售门票的海洋馆作为供货商一方，在市场中存在价格敏感游客的情况下，分析其与投机商之间的关系。我们通过对海洋馆与投机商之间进行的斯坦伯格博弈的分析，主要研究两个问题：一是了解海洋馆的定价策略与投机商的订货量之间的关系，二是关注价格敏感游客的作用，研究他们的消费行为对海洋馆和投机商所获利润的影响。研究结果表明，海洋馆的定价策略与投机商的订货量之间没有直接关系，而与价格敏感游客返回比例有关；投机商的订货量与价格敏感游客所占比例相关。

一、模型建立

为了简化模型，本文只考虑海洋馆和一个投机商，双方都符合理性人假设，且两成员对待风险的态度相同，均为风险中立的。

（一）定义和假设

A :海洋馆

B :游客

C :投机商

P0：海洋馆出售给游客的票价；

λ：投机商从海洋馆处购票所得的折扣，λ∈ ［ 0,1］；

：投机商出售给价格敏感型游客的票价；

：投机商从海洋馆处购得的折扣票的数量；

β：价格敏感型游客的比例；

θ：没有从投机商处购买到廉价票时返回海洋馆处购买的游客比例，θ∈ ［ 0,1］；

：独立决策下海洋馆的收益；

：集中决策下海洋馆的收益；

πA：协调后海洋馆的收益；

：独立决策下投机商的收益；

：集中决策下投机商的收益；

πC：协调后投机商的收益；

q1**：集中决策下投机商最优订货量；

λ⊗：集中决策下投机商从海洋馆处得到的最优折扣比例；

S1：独立决策下供应链的总收益；

S2：集中决策下供应链的总收益；

f(x)：游客到达的密度函数；

（二）模型介绍

模型中存在三方，海洋馆处于供应的一方，可视为供货商，游客属于需求的一方，投机商存在的目的只是为了转卖，希望通过低买高卖获取利润。海洋馆在有限的时间内销售有限的门票，游客到达海洋馆是一个连续的过程。

根据上述的博弈过程，投机商C的利润函数为：

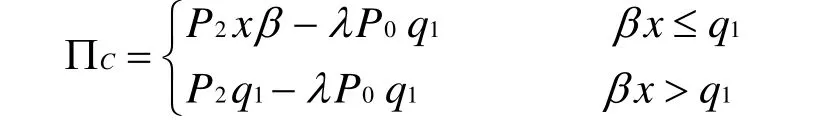
投机商C的期望利润为：

海洋馆A的利润函数为：

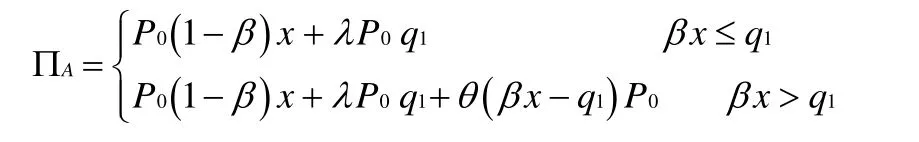
海洋馆A的期望利润为：

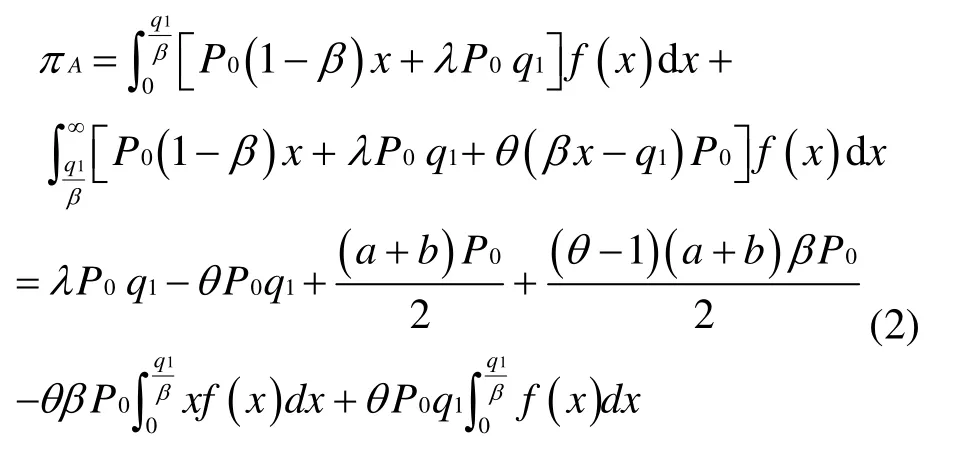
二、模型求解和分析

（一）决策模型

1．独立决策模型

独立决策模型是指市场中的双方以各自利益的最大化为目标，不考虑供应链整体利益的大小，即双方是一种非合作的关系。本文中，基于海洋馆与投机商都是完全理性的假设，两者独立决策时，海洋馆与投机商根据各自期望利润最大化的原则进行决策。

命题1:独立决策下，海洋馆给出的票价折扣力度越大，投机商的采购数量越大；游客中价格敏感型游客数量越多，投机商的采购数量越大。

证明：

对（1）式求q1偏导可得：

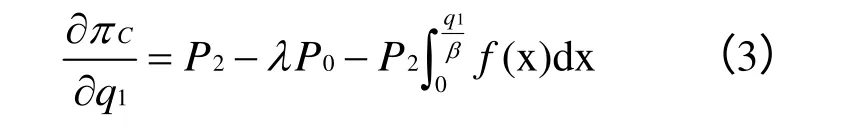
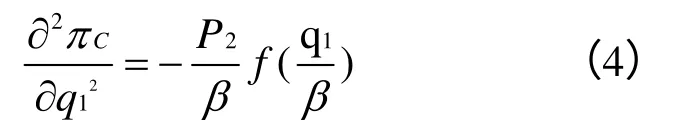
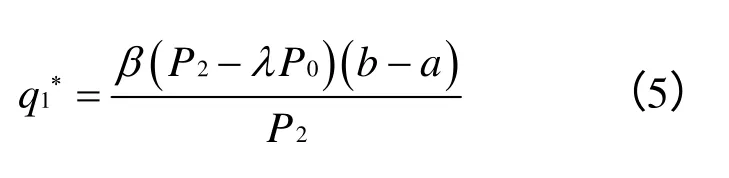
证毕。

所得q1*即为可以使投机商收益最大化的最优采购量，通过对q1*的分析可以看出，独立决策下，投机商的最优采购量与λ成负相关，与β成正相关。

命题2：独立决策下，当 2P2-θP0＞ 0时，伴随着从投机商处没有购买到门票的游客返回海洋馆进行购买人数比例的增加，海洋馆愿意给予投机商的折扣比例越小。

证明：

对（2）式求λ偏导可得:

将（5）式带入到（6）中后对λ再次求偏导得：

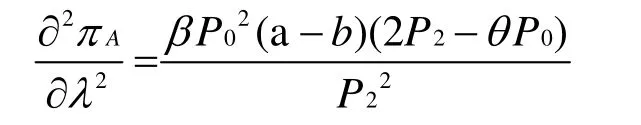
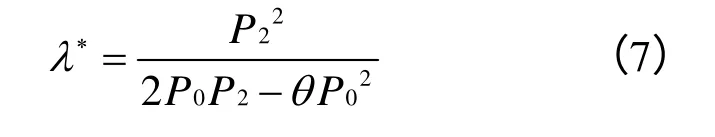
证毕。

这即是可以使海洋馆收益最大化的最优折扣价格。当 2P2-θP0>0时，供应链整体收益函数为凹函数，对（7）分析可以看出，海洋馆的最优折扣比例与θ成正相关。

命题3：独立决策下，价格敏感游客的数量越多，投机商所获得的收益越大。

证明：

将（5）式和（7）式分别代入（1）式和（2）式中，得：

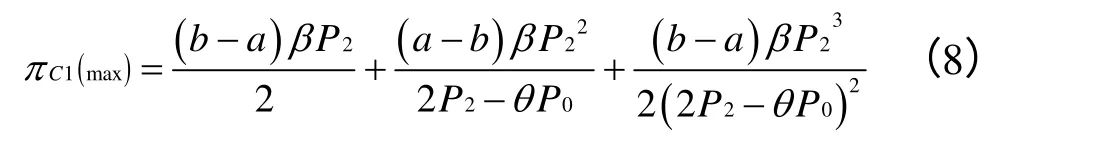
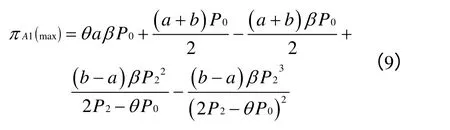
这两者是独立决策下投机商和海洋馆的最大利润函数，对（8）式进行分析可知，独立决策下，投机商的利润水平与β成正相关，即表示价格敏感游客的数量越多，投机商所获得的收益越大，这证明了命题3。

2．集中决策模型

在集中决策模型中，博弈双方从供应链的整体考虑，以实现双方总利润最大化为目标进行决策，博弈的双方是一种合作关系。

命题4：集中决策下供应链总收益大于独立决策下投机商与海洋馆双方最大收益之和，即S2＞S1。

证明：

对（8）式与（9）式求和得独到立决策下供应链的总收益S1的函数表达式为:

这即为集中决策下使整体供应链利润最大化的最优订货量。通过对（12）式分析可以看出，集中决策下投机商的最优采购数量只与敏感型游客的数量有关。

将（12）式代入（11）式中得到集中决策下供应链的总利润 2S为：

（13）式减去（10）式可得：

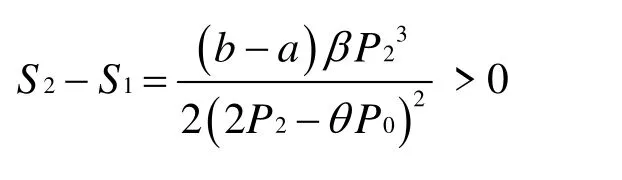
证毕。

3．决策模型比较分析

在集中决策下，将（12）式分别代入（1）式与（2）式中，得到投机商与海洋馆在集中决策下的收益分别为：

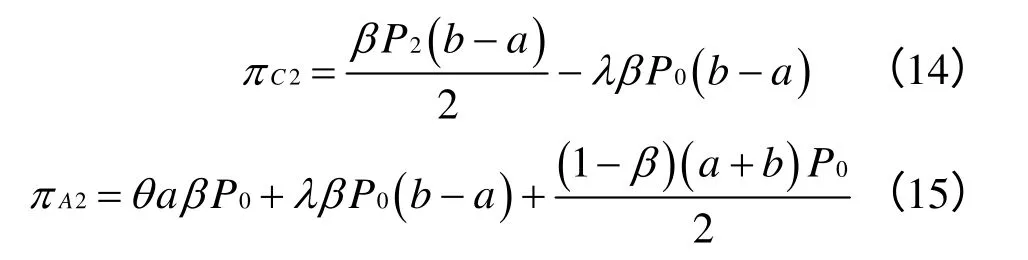
对（8）式和（14）式以及（9）式和（15）式分别进行对比分析可知，未协调前，集中决策下海洋馆和投机商获得的利润大小不能确定，其取决于θ的大小。

这就说明，在没有协调之前，虽然在集中决策下得到的供应链的总体收益大于独立决策时参与双方最大收益的总和，但是，此时并不能保证参与双方各自所获得的利润一定大于独立决策时的各自最大收益，这就表示，参与合作的双方都有背弃契约的可能性，合作的基础并不可靠。

（二）收益协调策略

由前面分析可知，未采取协调策略之前，集中决策下供应链的总收益大于独立决策下供应链的总收益，从最优化的角度来说，海洋馆与投机商应当采用集中决策下的折扣水平与进货量，但是，当供应链整体收益最大时，博弈双方并不是都获得了各自希望的最大收益，由结论4就可以看出，在集中决策下，投机商与海洋馆各自所获得的收益并不一定大于独立决策时获得的最大收益。这种情况下，投机商与海洋馆都是不会选择合作的，双方都有可能采用“败德行为”，以此来增加自己的收益。

如果希望博弈双方能够以供应链整体利益最大采取合作，那么这个问题即是博弈双方为了整体利益最大为目标而采取合作策略的Pareto有效协同下的博弈问题，博弈双方通过谈判形成一个Nash谈判解，确定相应的折扣比例，然后在这一契约的基础上，保证供应链整体收益最大化。这个协同方案可以实施的必要条件是，合作后的双方所获得的收益必须大于非合作策略下的各自的收益。对于本文所研究的情况而言，就是要找到一个均衡解λ⊗，这个λ⊗不仅可以使得供应链整体利益最大，而且可以使得博弈双方各自获得的收益不低于独立决策下两者的最大收益。只有这时，博弈双方才都不会采用“败德行为”。

下面我们来研究博弈双方如何来确定这个最终折扣力度λ⊗，这个又被称为Nash谈判解。Nash谈判解的生成必须满足以下条件：

1）合作中的双方在合作策略下的收益不能低于不合作时的收益，即ΔπA=πA2-πA1(max)≥ 0，ΔπC=πC2-πC1(max)≥ 0（具体公式参看（8）、（9）、（14）、（15）式）；

2）合作时的Nash谈判解存在，即max( ΔπA×ΔπC)存在。

令 Φ (λ)=ΔπA×ΔπC，由于 Φ (λ)是λ的函数，求其最大值就是令其对λ求导所得到的值为零，即：

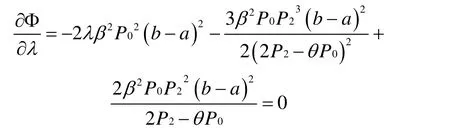
得到：

这即为本文所求的Nash谈判解。在这个解下，供应链可以获得整体最大收益，同时，参与双方的收益都比各自独立决策时获得的最大收益要大，这就达成了双方的“共赢”。

三、算例分析

假设某海洋馆销售门票，价格定为P0=100元，投机商售卖票价为P2=70元，β=0.4，θ=0.6，假设游客到达服从均匀分布，即x～ U ［ a,b］且x～ U ［1,100］。根据前面提供的模型解法，经过计算可以得到，独立决策下，海洋馆最大收益为πA1=3357.1875元，投机商最大收益为πC1=1082.8125元，供应链总收益为=4440元；集中决策下，协调之前，海洋馆收益为πA2=3885.6元，投机商收益为πC2=554.4元；协调之后，海洋馆收益为πA=3938元，投机商收益为πC=1302元，供应链总收益为=5240元。

可以看出，未协调之前，虽然海洋馆所得收益高于独立决策下的收益，但是投机商的收益却远远小于独立决策下的，一旦出现这种情况，投机商就会采取不合作的态度，并且海洋馆的收益也没有达到协调之后的高度，因此，协调是必须的。协调后供应链总利润高于独立决策下供应链总利润。供应链实现协调后海洋馆与投机商减去独立决策下各自的利润均大于零。

四、结论

供应链中参与各方之间的合作对供应链收益具有重要作用，怎样协调供应链中各个参与者的活动，从而达成各方的合作共赢，是研究供应链管理的重要课题之一。文章构建了独立决策模型和集中决策模型，并且利用博弈理论，在考虑价格敏感游客的基础上，对供货商和投机商收益分配和协调问题进行了探讨，证明了在集中决策下的总收益大于独立决策下的总收益，并由此对集中决策下的收益进行协调，使协调后的供货商和投机商的收益均大于独立决策下各自的收益，即实现了供应链的整体利益最大化和各方“共赢”，这对于当前的旅游供应链中的收益分配和协调问题的研究和实践具有一定的现实意义。最后需要说明的是，文章中建立的基础性模型简化或者忽略了许多现实中的因素，建立模型的主要目的在于为如何解决供应链中存在投机商时的利润最大化问题提供一定的思路与建议。

[1]ALFORD P.A framework for mapping and evaluating business process costs in the tourism supply chain [C].FREW A J,ed.Information and Communication Technologies in Tourism.Vienna:Springer Verlag,2005:125-136.

[2]TAPPER R,FONT X.Tourism supply chains:report of a desk research project for travel foundation[R].Leeds:Leeds Metropolitan University,Environment Business &Development Group,2004.

[3]SHEN Z J,SU X.Customer behavior modeling in revenue management and auctions:A review and new research opportunities[J]. Production and Operations Management,2007,16(6):713-728.

[4]TALLURI K,RYZIN G V.The theory and practice of revenue management[M].New York:Springer,2005.

[5]MING S X.Optimal pricing with speculators and strategic consumers[J].Management Science,2009,Articles in Advance:1-16.

[6]GUO Q.One game analysis of tour package fare and related phenomena in tourism supply chain in China[M].Toronto:UA Press,2008:137-142.

[7]YANG S,HUANG G Q,SONG H,et al.A game-theoretic approach to choice of profit and revenue maximization strategies in tourism supply chains for package holidays[J].Journal of China Tourism Research,2008,4(1):45-60.

[8]杨德礼,郭琼,何勇,等.供应链契约研究进展[J].管理学报,2006,3 (1):117-125.

[9]蔡建湖,周根贵,邵祖峰.季节性商品供应链的库存管理战略研究[J].商业研究,2009(2):1-5.