三通道偏振导航传感器正交误差影响分析

张宗梅 高晓颖 江云秋

1．宇航智能控制技术国家级重点试验室，北京 100854 2.北京航天自动控制研究所，北京 100854

利用偏振光进行导航定位是最近天文导航的研究热点，该技术通过检测与分析大气偏振图景信息，获得太阳、月亮等天体准确位置，从而实现系统载体的导航与定位。它具有自主性强、性能可靠、适用范围广和定位误差不随时间累计等特点，是一种具有重要应用潜力的导航定位技术。大气偏振检测技术是该导航定位技术的核心，因此，研究对其检测精度有影响的因素对提高系统导航定位精度具有非常重要的实际意义。本文主要针对已构建的三通道偏振导航传感器模型[1]，对模型中影响测量精度的偏振正交误差进行分析和研究。

根据沙蚁偏振光导航定位原理，已构建了偏振导航测试系统[1]。天空中的偏振光经过偏振导航传感器后将偏振光信号转换为电压信号，然后通过相关的信号处理系统，计算得出定位角。偏振导航传感器的结构如图1所示，图中所示为三通道偏振对立传感单元的结构示意图。每一通道的2个偏振片正交，3个通道的主偏振片的方向分别成0°,60°和120°。偏振对立传感单元由滤光片、偏振片、光电二极管和对数放大器组成，每一通道中2个偏振片的透光轴方向互相垂直。

图1 三通道偏振对立单元结构图

每个传感器的输出为：

S(Φ)=KI[1+dcos(2Φ-2Φmax)]

(1)

其中，K为放大倍数，I是光强，d是偏振光的偏振度，Φ是相对于太阳子午线目前的朝向，Фmax是使S(Φ)取得最大值的方向。

每个通道中的2个传感器的输出经过对数放大器后可以表示为

(2)

(3)

(4)

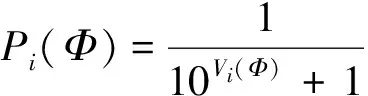
(5)

(6)

(7)

若采用式(5)和(6)解算则有

(8)

若采用式(5)和(7)解算则有

(9)

若采用式(6)和(7)解算则有

(10)

本文根据上述偏振导航测试系统分析了三通道内偏振光轴的相对正交误差对偏振定位角测量误差的影响，对构建偏振导航传感器具有实际的指导意义。

1 误差分析

理想情况下，每个通道中的2个偏振片应该完全正交(90°)，但在实际应用中一般都会存在一定的误差。设3个通道的偏振正交误差分别为：Δθ1,Δθ2,Δθ3，则偏振正交误差导致的待测定位角Ф的测量误差为：

(11)

(12)

(13)

又由(5)式得：

(14)

由(6)式得：

(15)

由(7)式得：

(16)

其中式(14)，(15)和(16)中的φ为测量系统的定位初始角。

由(8)式得：

(17)

(18)

由(9)式得：

(19)

(20)

由(10)式得：

(21)

(22)

分别将式(14)，(15)，(17)，(18)带入式(11)，将式(14)，(16)，(17)，(19)带入式(12)，将式(15)，(16)，(18)，(19)带入式(13)，则可求出ΔΦ1,ΔΦ2,ΔΦ3。

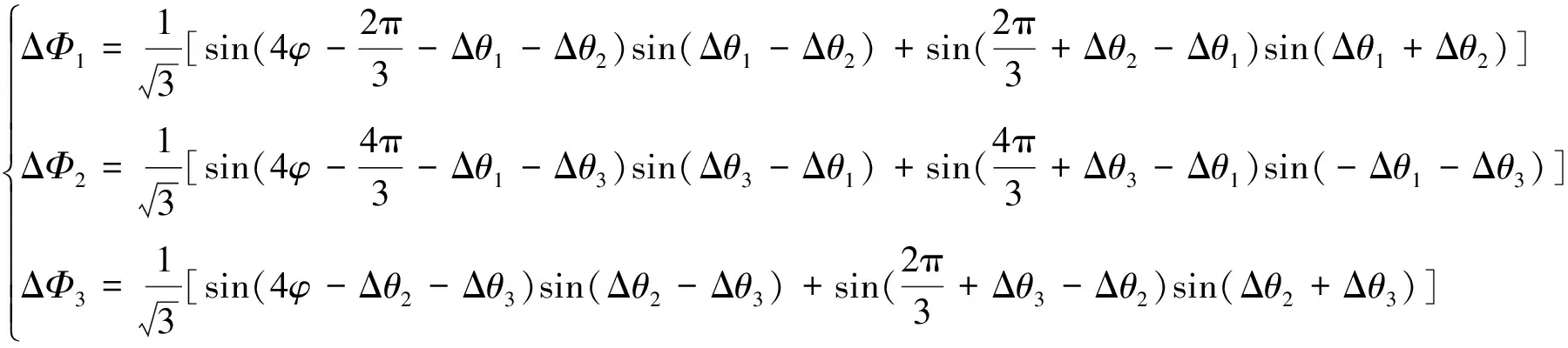
(23)

从而可得由偏振正交误差Δθi(i=1,2,3)引起的定位角Φ的测量误差：

(24)

此即为系统的定位角测量误差ΔΦ与3个通道的偏振正交误差Δθ1,Δθ2,Δθ3以及定位初始角φ的关系模型。

从(24)式可以看出，如果能通过处理使得3个通道的偏振正交误差满足Δθ1=Δθ2=Δθ3=Δθ，则误差模型可以简化为：

ΔΦ=ΔΦ1=ΔΦ2=ΔΦ3=sinΔθcosΔθ

(25)

特别地，当Δθ1=Δθ2=Δθ3=Δθ为小角度时，

ΔΦ=ΔΦ1=ΔΦ2=ΔΦ3≐Δθ

(26)

2 仿真和分析

(1)定位角测量误差与偏振正交误差的关系

图2和图3分别给出了当定位初始角φ为0°和30°时，定位角测量误差ΔΦ与3个通道的偏振正交误差Δθi(i=1,2,3)的关系。从图中可知，当φ分别为0°和30°，Δθ1从0°增加到2°，Δθ2从0°增加到4°，Δθ3从0°增加到6°时，ΔΦ分别从0°增加到 5.1665°和3.1112°。这说明，对于某一固定的定位初始角φ，随着偏振正交误差Δθ的增加，定位角测量误差ΔΦ也在单调增加。

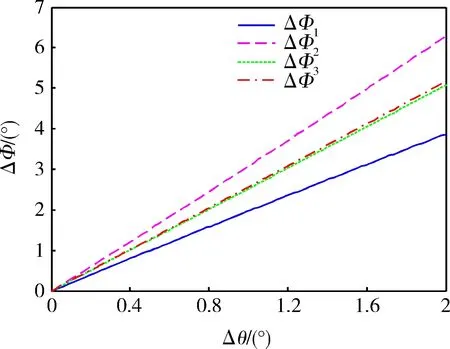
图2 定位初始角φ为0°时的情形

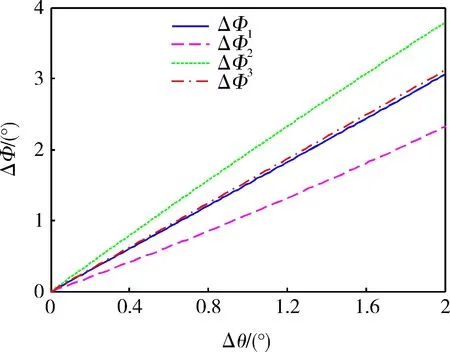
图3 定位初始角φ为30°时的情形

(2)定位角测量误差与定位初始角的关系

图4中给出的是偏振正交误差Δθ1=0.5°，Δθ2=0.1°，Δθ3=0.2°，φ从0°增加到360°时ΔΦ的变化关系。

图4 Δθ2=1°，Δθ3=2°时定位角测量误差与定位初始角的关系

图5中给出的是偏振正交误差Δθ1=0.5°，Δθ2=1°，Δθ3=2°，φ从0°增加到360°时ΔΦ的变化关系。

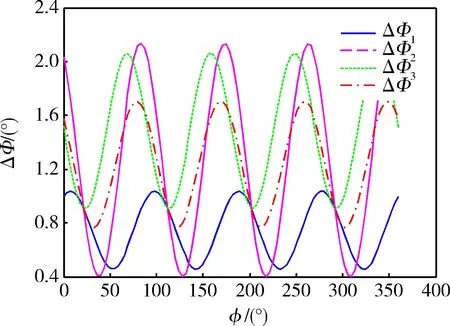
图5 Δθ2=1°，Δθ3=2°时定位角测量误差与定位初始角的关系

从图4和图5中可以看出，定位初始角的大小对定位角的测量误差存在一定的影响，在一个周期内(周期长度为π/2)角度误差先是随着方位角的增大而单调增大，后又随方位角的增大而减小。

图6给出了3个偏振正交误差相等(0°到0.6°)时，定位角测量误差与偏振正交误差的关系，从图中可以看出，定位角测量误差近似等于偏振正交误差。

图6 定位角测量误差与偏振正交误差的关系

3 结论

本文针对三通道偏振导航传感器测量系统模型中影响偏振方位角测量误差的误差源进行了分析，通过严格的公式推导了三通道间偏振光轴的正交偏振误差、定位初始角与定位角测量误差间的关系模型，对构建偏振导航传感器及精度的检验和改进具有实际的指导意义。

[1] 江云秋,等.基于偏振光的新型导航传感器研究[J].航天控制, 2011,29(3):91-94.(JIANG Yunqiu, et al.The Research of A Novel Navigation Sensor Based on Polarization Light[J].Aerospace Control, 2011,29(3):91-94.)

[2] 卢鸿谦,尹航,黄显林.偏振光/地磁/GPS/SINS组合导航方法[J].宇航学报, 2007, 28(4):897-902.(LU Hong-qian,YIN Hang,HUANG Xian-lin.Polarized-Light/Geomagnetism/GPS/SINS Integrated Navigation [J].Journal of Astronautics,2007, 28(4): 897-902 (in Chinese).)

[3] 褚金奎,等.仿生偏振导航传感器实验模型的构建与标定[J].微纳电子技术, 2007, 44: 376-378.(CHU Jin-kui,et al.Construction and Calibration for Bionic Navigation Sensor[J].Micronanoelectronic Technology, 2007, 44: 376-378 ( in Chinese).)

[4] 江云秋,等.偏振导航传感器建模与误差分析[J].弹箭与制导学报, 2009, 29(6):22-24.(JIANG Yun-qiu, et al.Model and Error Analysis of Polarization Navigation Sensor[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(6):22-24.)

[5] 黄旭锋,等.偏振正交误差对偏振光导航定位系统测量精度的影响[J].中国激光,2011,38(1): 0108002-1-0108002-5.(HUANG Xu-feng, et al.Effect of Polarization Analyzers Perpendicular Error on Measurement Accuracy of Polarization Position System[J].Chinese Journal of Lasers, 2011,38(1): 0108002-1-0108002-5.)

[6] Labhart T, Petzold J, Helbling H.Spatial Integration in Polarization-sensitive Interneurones of Crickets: A Survey of Evidence ,Mechanisms and Benefits[J].The Jounal of Experimental Biology,2001,204:2423-2430.

[7] Hartmann G，Wehner R.The Ant′s Path Integration System:A Neural Architecture[J].Biological Cybernetics, 1995,73(6):483-493.

[8] Collett M, Collett T S, Bisch S, et al.Local and Global Vectors in Desert ant Navigation[J].Nature, 1998,394(6690):269-272.

[9] Lambrinos D, Miller R, Labhart T, et al.A Mobile Robot Employ Insect Strategies for Navigation[J].Robotics and Autonomous Systems,2000,30(1):39-64.

[10] Wehner R.Desert and Navigation: How Miniature Brains Solve Complex Tasks[J].J Comp Physiol A,2003,189(8):579-588.