高动态条件下SINS信息在GPS软件接收机信号捕获中的应用*

黄国荣 许 刚,2 高 圆 彭兴钊 薛 冬

1. 空军工程大学航空航天工程学院，西安 710038 2.63767部队，西安 710038 3.西安交通大学材料科学与工程学院，西安 710049

卫星信号的捕获是卫星导航接收机中的一个重要信号处理过程。以GPS接收机为例，信号捕获是指实现对码相位、载波频率(含多普勒频移)和卫星PRN码的三维搜索[1-2]。信号搜索是通过卫星信号和本地信号进行相关计算完成的。在搜索过程中，对所搜索的卫星信号移动本地码和本地载波频率，当本地C/A码的码相位、本地载波频率和输入信号中的码相位及载波频率相匹配时，相关输出值最大，完成捕获。

目前广泛使用的自主搜索算法包括串行搜索法、并行码相位搜索法和并行频率搜索法等[1-2]。在高动态条件下，由于载体和卫星之间存在高速运动，使卫星信号产生很大的多普勒频移，进而使频域带宽及频域搜索点的个数显著增加。而自主搜索算法只能被动地接受这一现实，导致搜索范围变大和时间延长，这在一定程度上限制了卫星导航接收机在高动态环境下的使用。

随着GPS软件接收机和惯性/卫星组合导航技术的发展，为解决高动态条件下卫星导航接收机信号捕获问题提供了新的思路和方法。本文在SINS/GPS松组合框架下研究利用惯导信息辅助接收机信号的捕获问题。首先分析了GPS软件接收机自主搜索算法中的并行码相位搜索算法的基本原理[1-3]，推导了捷联惯导系统(SINS)信息在GPS软件接收机信号捕获中的作用[2,4]，在此基础上建立了基于SINS辅助GPS接收机信号捕获思路的SINS/GPS松组合模型[4]，提出了一种外部信息辅助的卫星信号搜索算法，通过仿真实验证明该搜索算法可快速有效地实现高动态GPS信号的捕获。

1 并行码相位搜索算法原理

并行码相位搜索算法将需要搜捕的频率范围等分成若干个频率段，在每段频率上只需要进行一次搜索就可以确定C/A码的初始相位，即将二维搜索转化为一维搜索，捕获过程中的运算量最小、速度最快，因此，当前进入实验阶段的GPS软件接收机的捕获算法多采用并行码相位搜索算法。

并行码相位搜索算法利用快速傅立叶变换处理循环相关操作。设长度有限且为N的序列x(n)和y(n)的离散傅立叶变换分别为：

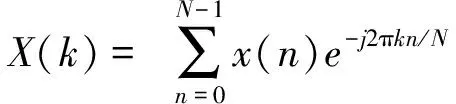
(1)

则x(n)和y(n)的互相关序列为:

(2)

去掉比例因子1/N，z(n)的N点离散傅立叶变换为：

(3)

并行码相位搜索算法框图如图1所示。输入信号与本地的载波信号相乘得到I支路信号，与90°相移后的本地载波相乘后得到Q支路信号，I支路和Q支路信号组合得到复信号x(n)=I(n)+jQ(n)，x(n)经过傅立叶变换后与经过傅立叶变换的本地C/A码相乘，输出结果经过傅立叶反变换转换为时域信号，傅立叶反变换输出的模值表示输入信号与本地C/A码的相关结果，若结果中出现峰值，其位置即是输入信号的码相位。

图1 并行码相位搜索算法

根据GPS实测数据，得到4号星和7号星捕获结果如图2(a)和图2(b)所示，7号星的捕获结果没有明显的峰值，在整个频率范围内幅值表现出明显的随机性；而4号星可见明显峰值，说明4号星信号包含在采集数据内，其粗略载波频率和码相位可以通过分析图2(b)的数据得到，从而完成捕获所要达到的目标。

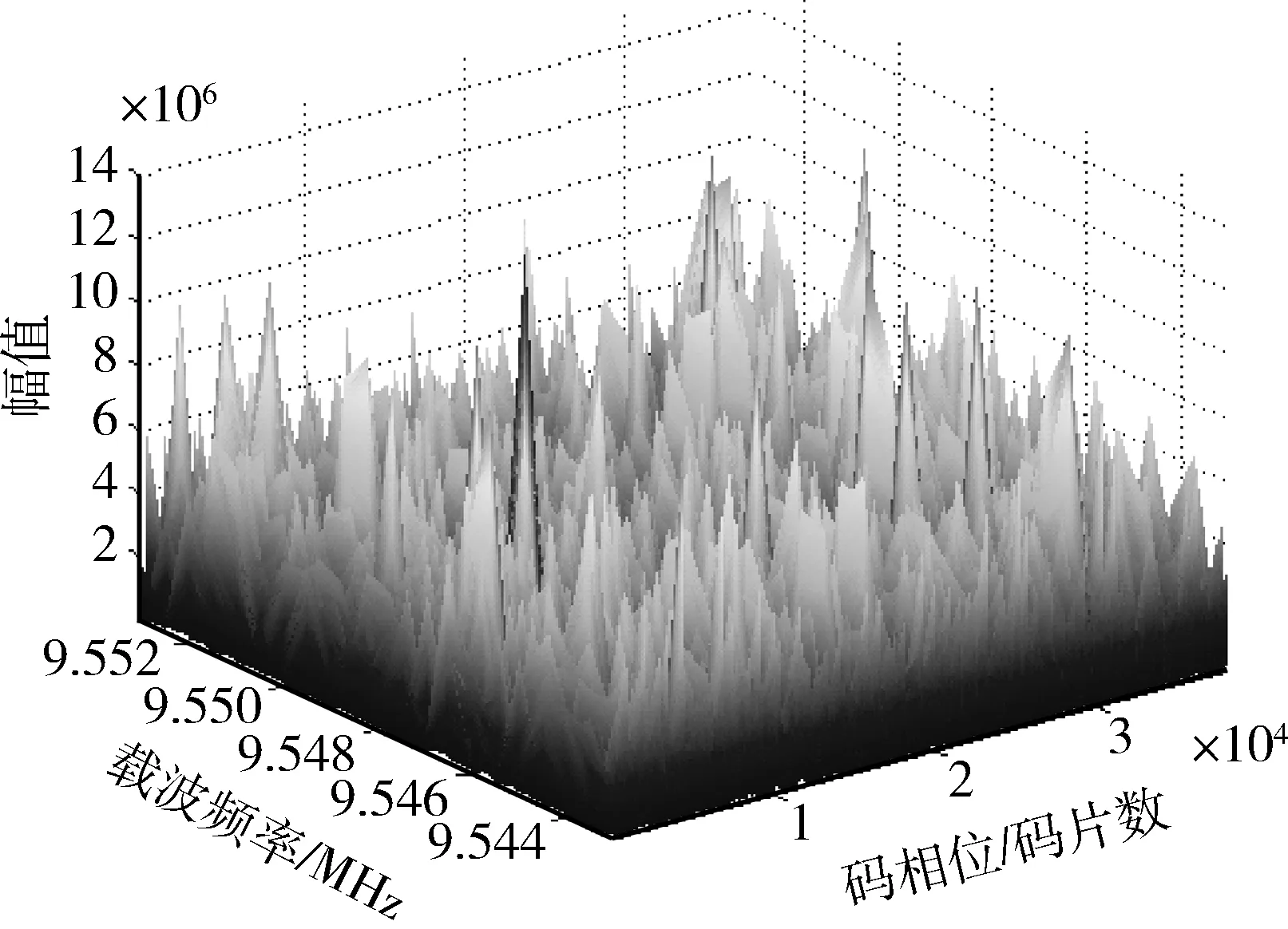
图2(a) 7号星捕获结果

图2(b) 4号星捕获结果

2 SINS辅助GPS软件接收机信号捕获原理

2.1 卫星信号的多普勒效应

用户接收机与卫星的相对运动速度可引起载波频率的变化，即多普勒频移fd，fd对接收机信号的捕获有重要影响。理论分析可得：

(4)

fr为L1载波频率1575.42MHz，vd为相对运动速度，c为光速。

GPS卫星运行周期为11h58min2.05s,从卫星轨道的近似半径可以得到卫星的角速度dθ/dt和速度vs：

1.458×10-4rad/s

(5)

(6)

其中，Vs,Rs分别代表卫星速度和卫星轨道半径。

如图3所示，在用户静止时，卫星相对用户的卫星角速度vd引起了多普勒，且：

vd=vssinβ

(7)

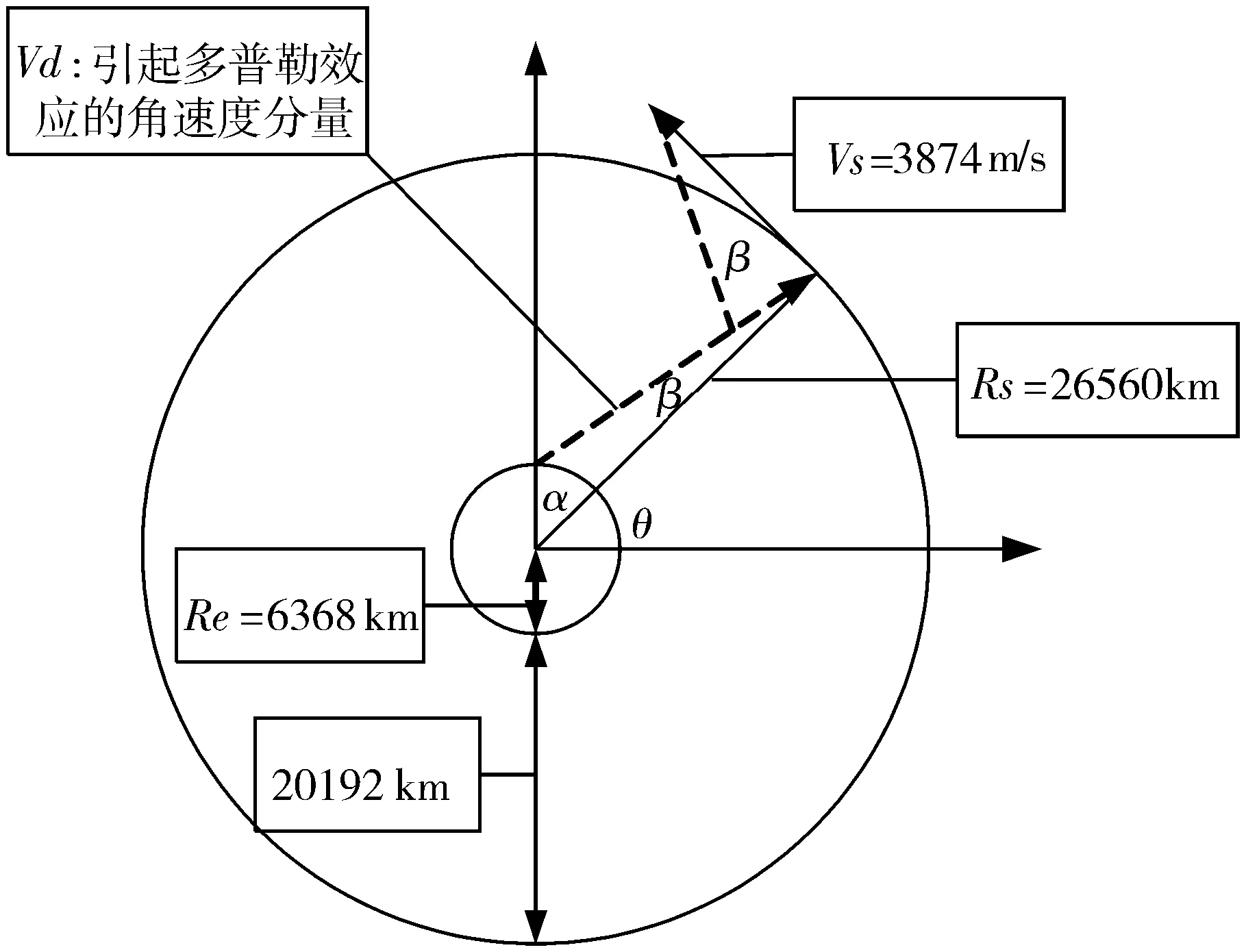
图3 卫星运动引起的多普勒频移

根据卫星轨道速度，取水平方向的最大值，得到多普勒速度的最大值：

(8)

则该速度引起的多普勒频移为：

(9)

因此，对于一个地面固定观测器来说，最大的多普勒频移是±5kHz。

GPS信号中的粗定位码即C/A码的一个完整周期包含1023片码元，如果采用并行码相位搜索算法，设频率搜索步长为0.5kHz，码搜索步长为0.5码元，且假定一次搜索时间为T1，则在±5kHz多普勒频移条件下，完成搜索的时间T为：

(10)

如果地面GPS接收设备高速运动，当前929m/s的速度几乎可以包括所有飞行器，所以载波的多普勒频移就应扩至±10kHz。基于上述假设条件，完成一次搜索的时间就应达到81840T1，是地面固定接收设备的2倍，从而可能导致接收机的捕获时间过长，而达不到实际应用的要求。

2.2 SINS信息辅助接收机信号捕获原理

GPS接收机的高速运动导致载波多普勒频移的范围扩大，即增加了载波多普勒频移的不确定性。为了解决该问题，提升接收机的硬件性能是当前的一个主要解决方法，而这种方法会增加系统的应用成本。目前，在各种航空器导航领域主要采用组合导航的形式，并且以SINS/GPS组合为主。所以采用SINS信息提前预估载波频率的多普勒频移，进而减少频率搜索空间，是提升接收机性能的一种具有重要意义的思路和方法。

在SINS辅助下，多普勒频移域搜索的起点可取为SINS估计的下一个时刻对应的多普勒频移值。由于SINS导航解算误差、星站时钟频率漂移等因素的存在，估计的多普勒频移并非理想的多普勒频移捕获值，因此需在中心点附近做进一步搜索，搜索范围的设定应考虑上述误差因素的影响。根据GPS接收机不同的启动条件，多普勒频移域搜索起点及范围的估计具有不同的形式，现分别予以讨论。

1)冷启动

由于GPS接收机在冷启动条件下没有任何的星历和历书信息，可见卫星、接收机位置和接收机时钟均为未知数[5]。因此，冷启动的捕获过程事实上是三维搜索过程，即卫星搜索方向、多普勒频率搜索方向和码相位搜索方向。在卫星搜索方向采用的是“满天搜索”方式，即搜索所有可能的PRN码，直到搜索到卫星为止。为研究方便，本文假设冷启动时可直接搜索到卫星。在多普勒频移方向，由于卫星星历、历书和接收机时钟漂移未知，故多普勒频移域搜索的起点可近似根据SINS估计的载体速度所产生的多普勒频移计算,即：

(11)

多普勒频移域的搜索范围根据卫星运动产生的最大多普勒频移、SINS的导航解算误差及星站时钟频率漂移进行估计。

接收机时钟通常采用较低精度的温补可调型晶振[6]，其频率漂移可通过微调和温度补偿来克服，标称频率为10MHz，频率稳定度为百万分之四，由频率漂移所引起的多普勒频移约为6500Hz。因此，冷启动条件下多普勒频移域的搜索范围±Δfac(Hz)可设为：

(12)

2)温启动及热启动

GPS接收机在温启动条件下存储最近几天内卫星的历书、用户的大概位置和用户对GPS时间的估计，据此可推算出卫星在当前时刻的位置、速度及其多普勒频移[5，7]，并由用户的大概位置确定可见星；在热启动条件下接收机不仅含有卫星的历书、用户的位置和精确的GPS时间，还含有卫星的有效星历。因此在温启动及热启动条件下，多普勒频移域搜索的起点可根据下式估计：

(13)

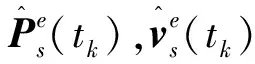
在温启动条件下通过最近的卫星历书所推算的卫星多普勒频移fsv通常有偏离真实值±150Hz的误差[5]。在前一次启动时接收机的频漂已经计算，可直接用于温、热启动条件下的快速捕获。另外，由于SINS估计的载体多普勒频移误差通常小于50Hz，因此在温启动条件下多普勒频移域的搜索范围±Δfac1(Hz)可设为：

(14)

(15)

3 基于SINS信息辅助GPS软件接收机信号捕获的SINS/GPS松组合模型

为了研究SINS信息对GPS软件接收机信号捕获的辅助作用和辅助后接收机的性能，构建基于SINS辅助GPS的SINS/GPS松组合模型如图4所示。其中，以SINS为主导航系统，GPS提供位置、速度信息通过卡尔曼滤波器估计和修正SINS的累积误差，抑制SINS误差的发散，提供相当于GPS系统精度的位置、速度信息，并对姿态误差和惯性元件误差进行估计与修正。其中虚线部分代表SINS信息对GPS的辅助通道，是完成载波多普勒频移估计和GPS软件接收机搜索频率起点初始化的关键。

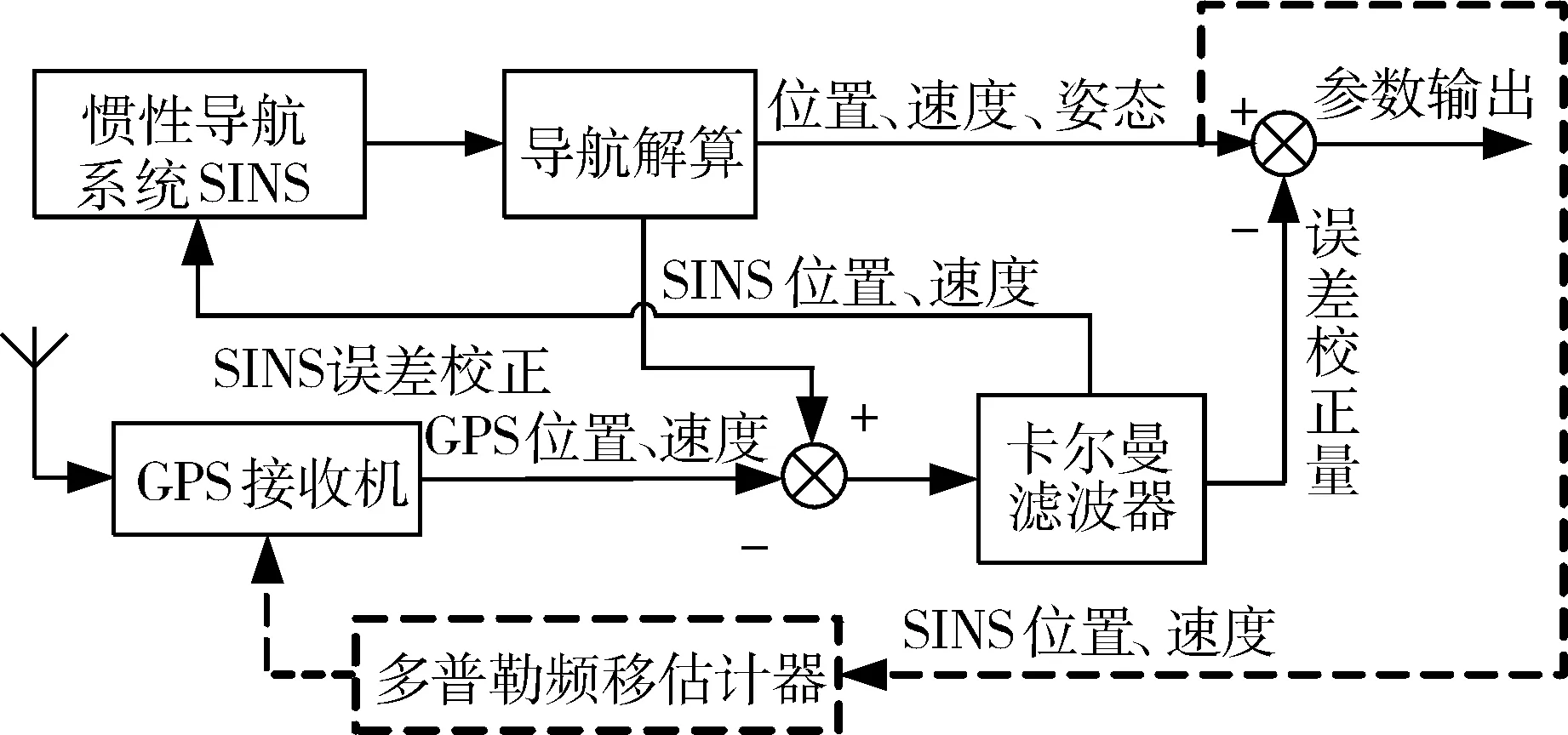
图4 SINS/GPS松组合模型

采用SINS位置、速度和GPS位置、速度的差值作为量测值，则观测向量为：

(16)

其中，R=[Lλh]T是载体位置向量，V=[VEVNVD]T为载体速度向量。系统状态向量取为X=[φnδVnδLδλδhδεn▽n]T。

故松组合导航卡尔曼滤波模型为：

Z=HX+V

(17)

式中，A为15×15阶状态矩阵；H为6×15阶观测矩阵；G为6×15阶系统噪声驱动矩阵，W为6维系统噪声矩阵，由陀螺仪和加速度计噪声构成；V为6维观测噪声矩阵，由GPS观测噪声构成。

4 仿真实验分析

4.1 GPS信号仿真

卫星信号是接收机捕获算法的基础，由于采用硬件电路采集真实卫星信号需要一定的研制成本和研制周期，且仿真方法的灵活性对研究接收机基带数据处理的各种算法具有先天的优势。因此，本文根据GPS卫星信号的结构，基于MATLAB/SIMULINK搭建了如图5所示的GPS卫星信号产生器。其中C/A码、导航数据、载波和最终的卫星信号仿真结果如图6所示。采用该信号产生器输出的信号完成后续算法的研究。

图5 GPS卫星信号产生器的SIMULINK模型

图6 GPS卫星信号及其组成部分

4.2 外部信息辅助搜索算法的性能分析

仿真参数设置如下：设惯性导航系统的陀螺随机常数为0.1(°)/h，随机漂移均方差为0.1(°)/h，一阶马尔可夫噪声驱动白噪声均方差为0.1(°)/h，相关时间为3600s，加速度计一阶马尔可夫噪声驱动白噪声均方差为10-4g，相关时间为1800s，加速度计白噪声均方差为10-5g，GPS随机伪距误差为8m，随机伪距率测量误差为0.05m/s。

各个子系统和组合导航的解算周期为：飞行轨迹采样周期为T=0.01s，捷联解算周期为2T=0.02s，GPS定位和测速周期为100T=1s，组合导航周期取为100T=1s，即每50个SINS解算后进行一次数据融合，也即与GPS定位和测速解算周期相一致。

飞行轨迹设为一高速匀速平飞过程，其初始参数为：纬度35°、经度110°、高度8000m，航向角60°、俯仰角0°、滚转角0°，飞机机体系纵轴速度930m/s(3348km/h)，飞行时间60s。

表1 2种算法的捕获时间

在仿真实验中，基于MATLAB平台，在同一台计算机上采用2种方法对同一段卫星信号进行处理，得到2种算法的时间性能如表1所示。其中执行时间没有采用绝对时间，因为在当前的计算机平台上各种算法并不是实时执行的，绝对时间仅仅是近似的，而采取相对值则可以说明哪种算法实时性更好。因此，在设定自主搜索算法执行时间为单位1的前提下，得到了SINS辅助搜索算法的执行时间为0.42，小于自主搜索算法。但是，由于SINS辅助搜索算法采用的信息要多于自主搜索算法，其算法复杂性要明显大于自主搜索算法。

由于SINS辅助搜索算法只是提供了多普勒频移的估计值和载波捕获的初始起点的近似值，仅仅是提高了算法的搜索速度，并没有改变自主搜索算法的搜索结构，因此，2种算法的捕获精度是相当的。实验结果也验证了上述结论，如表2所示。

表2 2种算法捕获精度

5 结语

针对卫星导航接收机载体在高速度条件下面临的特殊信号捕获问题，提出了一种外部信息辅助的搜索算法，并在软件接收机和SINS/GPS松组合模型下构建了该算法的模型。经过仿真实验验证，该算法相对传统的自主搜索算法在提供相同精度的前提下可提高搜索速度达一倍以上，从而解决了高动态条件下卫星信号的捕获问题，具有重要的理论和工程应用价值。

[1] 杨东凯，张飞舟，张波，译.软件定义的GPS和伽利略接收机[M].北京：国防工业出版社,2008.

[2] 董绪荣，唐斌，蒋德.卫星导航软件接收机原理与设计[M].北京：国防工业出版社，2008.

[3] 刘娣，薄煜明，赵高鹏.GPS软件接收机信号的快速捕获与跟踪[J].计算机工程，2010，36(1)：239-241.(LIU Di,BO Yu-Ming，ZHAO Gao-Peng.Fast Acquisition and Tracking for Signal of GPS Software Receiver[J].Computer Engineering，2010，36(1)：239-241.)

[4] 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，1998.

[5] Peter R，Nicolaj B.Design of a Single Frequeney GPS Software Receiver[D].MSc，Aalborg University，2004，06.

[6] 李伟,胡丛玮.GPS软件接收机信号特征分析[J].测绘信息工程，2008，33(5): 1-2.(Li Wei，Hu CongWei.Signal Analyzation of Software GPS Receiver[J].Journal of Geomatics，2008，33(5): 1-2.)

[7] 张伯川,张其善,常青.高动态接收机的温启动快捕问题研究[J].电子学报，2005,33(3): 530-533.(Zhang Bo-Chuan，Zhang Qi-Shan，Chang Qing.A Satellites Signals Quick Acquisition Algorithm for the High Dynamic GPS Receivers in Warm Start[J].ACTA Electronic Sinice,2005,33(3): 530-533.)

[8] 薛文芳.高动态GPS接收机设计中几个关键问题的研究[D].北京航空航天大学，2002.

[9] 唐康华,吴美平,胡小平.MEMS IMU辅助的高性能GPS接收机设计[J].测绘学报，2008，37(1):128-134.(Tang KangHua，Wu MeiPing,Hu XiaoPing.Design of MEMS IMU Aided High-performance GPS Receiver [J].Acta Geodaetica et Cartographica Sinica，2008，37(1):128-134.)

[10] 秦永元,俞济祥.惯导速度辅助下GPS接收机码环的噪声响应和动态跟踪性能分析[J].航空学报，1990，11(12):47-52.(Qin YongYuan，Yu JiXiang.Noise Response and Manoeuvre Tracking Performance Analysis for the Coherently Operating GPS Receiver Code Loop Aided by the INS Velocity[J].Journal of Chinese Inertial Technology，1990，11(12):47-52.)

[11] 秦永元.GPS载波环的惯性速度辅助及SA建模探讨[J].航空电子技术,1995，79(2):8-13.(Qing Yong-Yuan.GPS Carrier Ring Inertial Velocity Auxiliary and SA Modeling to Explore[J].Avionics Technology，1995，79(2):8-13.)

[12] 薛巍,向敬成,周治中.一种PN码捕获的门限自适应估计方法[J].电子学报，2003，31(12): 1870-1873.( Xue Wei，Xiang JingCheng，Zhou ZhiZhong.An Adaptive Threshold Estimation Method for PN Code Acquisition[J].ACTA Electronica Sinice，2003,31(12): 1870-1873.)