立式罐罐底不平度修正值的测量与计算

廉永胜 张耀峰 南美雄 李汲峰 龚新强

(1.山西省大容量计量站，运城 044000；2.长庆油田技术监测中心，西安 710021)

0 引言

立式罐是我国规定的国际间石油化工产品贸易结算的强检计量器具。它的容量计量准确与否，直接关系到国家及企业的经济利益和计量信誉。而要准确地计量立式罐容量，给出液位h与相应的容量V(h)之函数用表，必须涉及到罐底不平度修正值(总量与部分容量)的测量与计算问题。JJG168-2005《立式金属罐》给出的测量与计算公式只能准确地求得其总量，而不能准确地求其部分容量，若将容量按其高度平均求部分容量，则将导致较大的误差。为此，作者提出了总量与部分容量皆准确的新测量与计算法。

1 测量与计算

立式罐罐底通常设计成平底，但由于施工焊接应力的变化和使用基础不均衡下沉等影响，罐底形成了中间高、四周低凸凹不平状态，如图1所示。

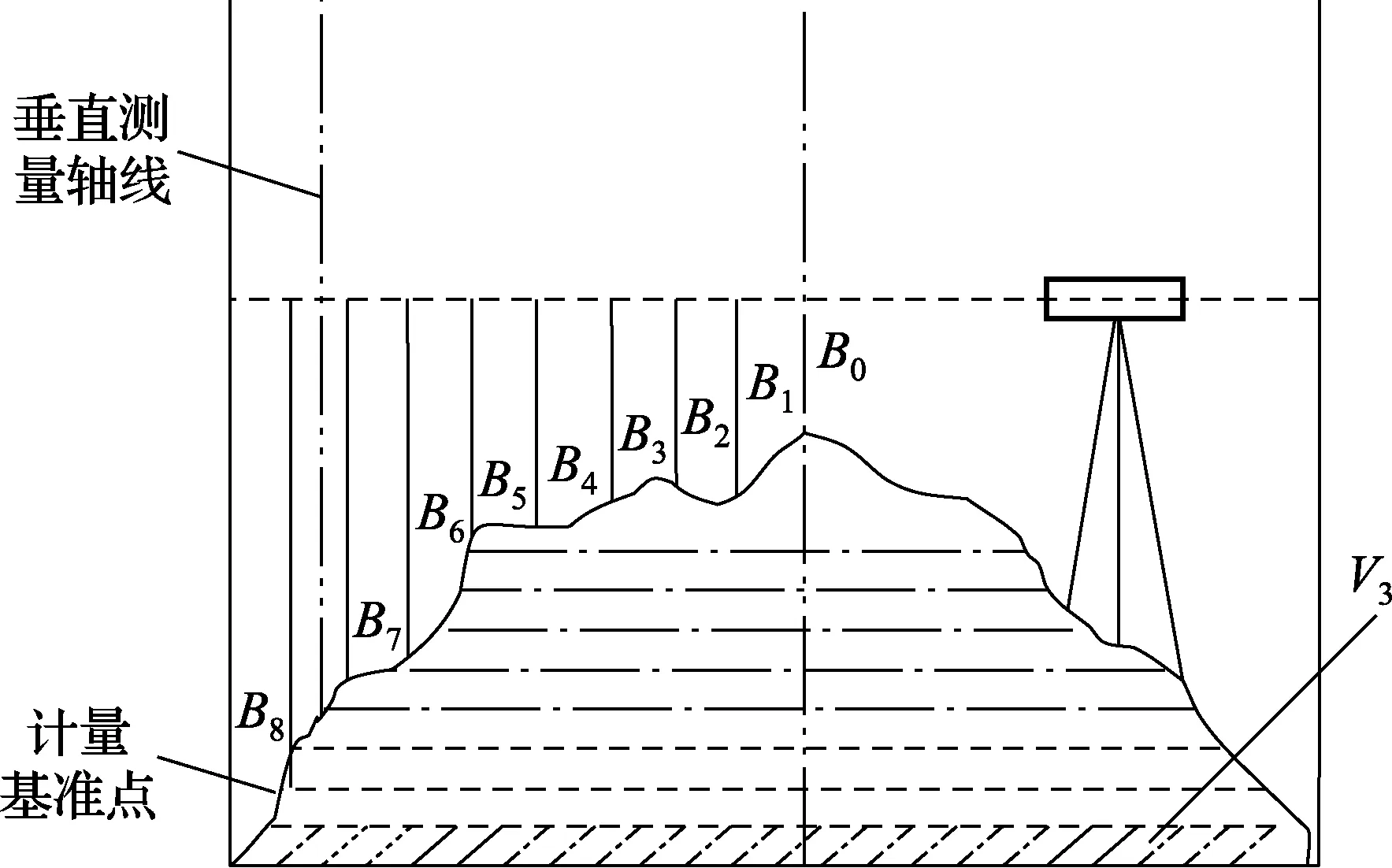
图1 罐底不平度水准测量

罐底不平度修正值是相应于罐圆柱形部分所排除的体积(图1中虚线所示的体积)。为计算该体积，可把该体积分成若干个区段，即以一个水平平面截割该体积成除第一个区段视为圆锥外，其他区段为一个相应的圆台。将这些区段的体积累加起来即为罐底不平度修正值的总量。各区段的高度均很小，完全可视为一个规则的圆台，区段分割得愈多，这种逼近的程度愈高(愈精确)。

1.1 测量点的标记

测量点的标记就是在罐底上确定的同心圆(Ⅰ，Ⅱ，…,m)和半径(0-1，0-2，…，0-n)交点的位置，如图2所示。测量点的数目由罐底不平度修正值所需精度与罐底凹凸不平的程度来确定。从罐底中心到同心圆周的距离是根据所分圆环面积相等的条件决定。

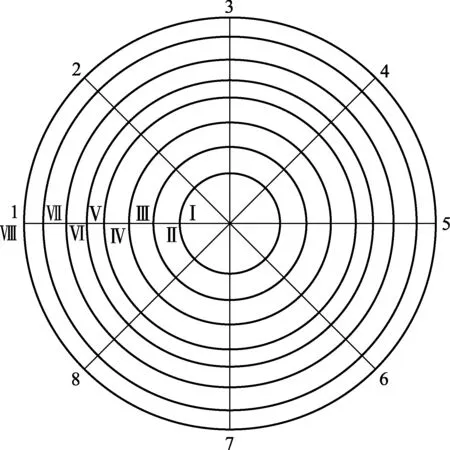
图2 测量点的标记

设罐的半径为R，共分成m个圆环，它们圆周的半径从里到外依次为R1，R2…，Rm，因各圆环面积相等，故有：

(1)

(2)

1.2 罐底的水准测量

测量用DS3型自动安平水准仪进行。由表1示例可知，水准尺上的读数Bi相应于罐底各测点到水准仪的水准平面之间的垂直距离。

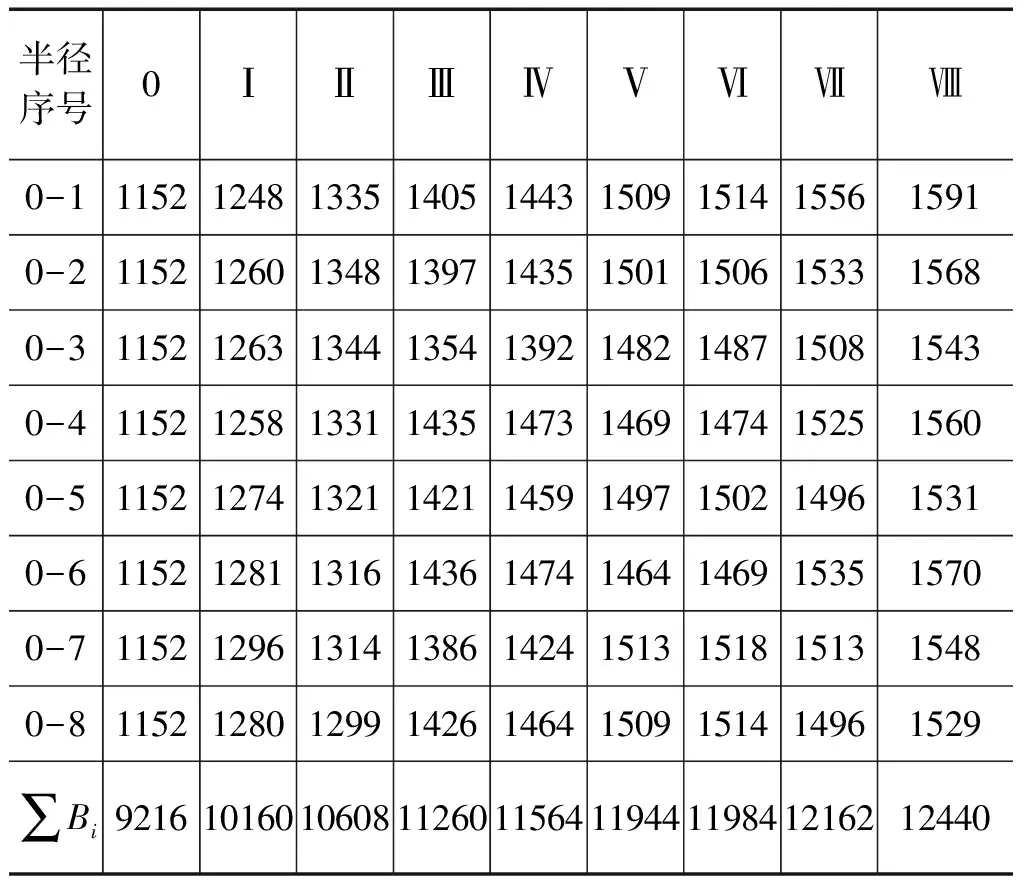
表1 [罐底的水准测量数据] mm

1.3 罐底不平度修正值的计算

我们将不平度修正值区段按精度所需分割成若干个不同的小区段，中间小区段为一圆锥，其余皆为小圆台，锥底半径和各圆台上底与下底半径分别如式(2)所示。于是，这些小区段的体积分别为：

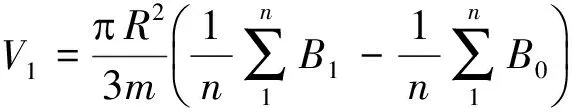
(3)

(4)

(5)

式中：k=mn

于是，罐底不平度修正值总量为：

(6)

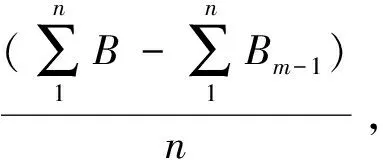
(7)

测量出罐的计量基准点至罐中心最高点之距离h0，依据式(7)并以累加的方式对罐的容量进行修正，即可求得该距离h0区段内的部分容量，即求得厘米(或毫米)容量表。

这里需要指出，对个别中间低四周高的罐，式(5)、(6)、(7)均适用，只是区段量平均高度取绝对值。

2 实测举例

某一立式金属罐的半径R=17.000m，罐底不平度修正值测量时各测点水准尺上的读数Bi(mm)列于表1，求其底量不平度修正值。在通常情况下，取m=n=8。依据式(5)求得各区段罐底不平度修正值V1～V8为：4.4639，9.351，22.968，15.043，24.208，3.1167，16.397，29.556m3。

将以上各值相加，即得罐底不平度修正值总量为：

该计算结果与我国现行规程JJG168-2005计算结果相一致。

上述各区段每毫米平均的不平度修正值V1,mm～V8,mm为：0.0378，0.16698，0.2818，0.3959，0.5096，0.6234，0.7369，0.8505m3/mm。

将上述各区段毫米容积累加起来对底量进行修正，即可得到底量的毫米容积表。

若按总量取平均，则总量区段的平均毫米容积为：

可见，若以总量区段的平均毫米容积以累加方式对底量进行修正，将会产生较大的误差。

3 结论

本文提出的罐底不平度修正值的测量与计算，称为圆台分隔叠加法。用该方法求得的罐底部分容量精度比通常的圆柱分隔法高。

参考文献

[1] 廉育英，等.立式金属计量罐大容量新测量方法的研究.计量学报，1988(4)：241-247

[2] 廉育英.容量与密度计量.北京：机械工业出版社，1990

[3] 廉育英著.容量计量技术.北京：中国计量出版社，2007

[4] JJG 168—2005立式金属罐