改进三平面互检法中测量位置的定量分析

郑显锋 郑 颖 田爱玲

(1.西安航天计量测试研究所，西安 710100；2.西安航空学院，西安 710065；3.西安工业大学光电工程学院，西安 710032)

0 引言

随着科学技术的飞速发展，在生产、研究以及高端技术领域中，对光学元件的精度提出了新的要求，高精度光学元件已成为支撑一些领域发展的重要部件，所以高精度光学元件也需要与之相对应的高精度检测方法。

目前，干涉法是用于高精度光学元件检测最主要的方法，为了提高检测精度，需要对参考面进行绝对检测。在三维面型的绝对检测中改进三平面互检法的可行性已经得到验证，其检测结果与ZYGO干涉仪中“three-flat”检测结果的PV值误差小于0.001l。为了进一步减小误差，对改进三平面互检法中旋转测量次数对最终检测结果的影响进行了研究，发现不同测量位置的影响也是不同的，有的测量位置的测量次数需要达到18次或者以上才能保证偏差值小于0.0001l，而有的测量位置的旋转测量次数仅需要达到8次就可以满足偏差值小于0.0001l的要求。为了更好的完善改进三平面互检法，需要定量分析其测量位置对最终检测结果的影响，得到不同测量位置的检测标准和操作指导。

1 改进三平面互检法检测原理

干涉法测量过程中总存在一个面作为参考面、另一个面作为测试面，如图1中第1组测量所示，在这组测量中参考面为平面B，测试面为平面A。改进三平面互检法如图1所示由4组测量组成，其测量次序为：(BA，BAR,CA,CB)，平面A、B、C的三维面型均可以得到。这种方法测量次序中的第2组测量为1组特殊的测量，参考面为平面B，测试面为平面A的旋转不变部分。

由图1可得：

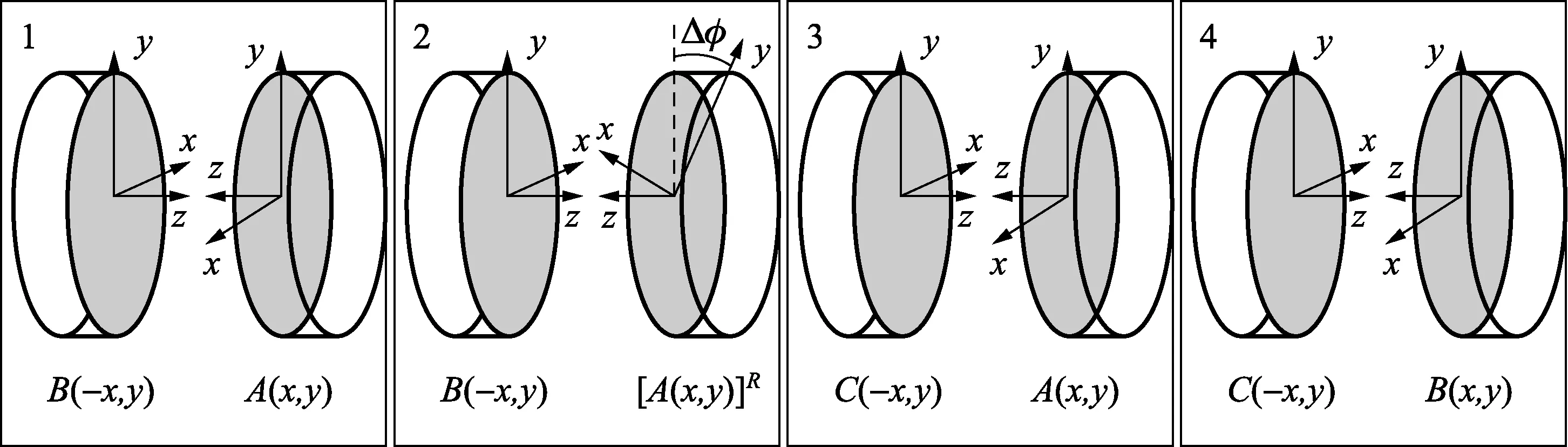
图1 改进三平面互检法测量次序

(1)

式中，W1(x,y)、W2(x,y)、W3(x,y)、W4(x,y)分别表示第1、2、3、4组的测量结果；WA(x,y)、WB(x,y)分别表示平面A、平面B的面型(与预订坐标系一致)；WB(-x,y)、WC(-x,y)分别表示平面B、平面C的面型(在预订坐标系中沿y轴进行了一次翻转)；[WA(x,y)]R表示平面A的旋转不变部分。

最终可以得到平面A、B、C的三维面型：

(2)

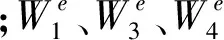
从理论上可知旋转测量次数会对检测结果有较大的影响。由旋转测量次数对最终检测结果影响的研究表明：在相同旋转测量次数的情况下，不同测量位置的检测结果对最终的检测结果的影响不同。有必要对测量位置的影响进行专门的研究。

2 比对实验设计

对测量位置的影响进行研究，首先对改进三平面互检法中的三个平面的位置进行定义，本文中对应第1节中的改进三平面互检法理论中对应的平面A、B、C，根据其在测量过程中的所起作用不同，定义如下：平面A为旋转平面；平面B为参考测试平面；平面C为完全参考平面。

确定实验中的3个平面。如图2(a)所示为1号平面，口径为100mm的ZYGO干涉仪原装石英标准镜头；图2(b)所示为2号平面，国内生产的口径为100mm的ZYGO干涉仪石英标准镜头；图2(c)所示为3号平面，口径为150mm的ZYGO干涉仪原装石英标准镜头，通过一个转接头进行转换，实验测量中只使用其100mm口径部分。

图2 选取的测量平面

设计3组对照实验，令3个平面分别作为完全参考面。为了不引入其他误差，将3组实验设计在同一个实验测量中。3组实验分别为：实验一、实验二和实验三，与理论中的表述对应如下：

实验一：平面A——1号平面、平面B——2号平面、平面C——3号平面。

实验二：平面A——3号平面、平面B——2号平面、平面C——1号平面。

实验三：平面A——2号平面、平面B——3号平面、平面C——1号平面。

3组实验中3个平面的位置对照如表1所示。

表1 3组实验中3个平面的位置对照表

为了更直观的观察到不同位置引入的影响，它们的旋转测量次数均为8次(每次旋转45°，旋转一周)。另外，出于综合分析的目的，在实验一中多一组旋转测量次数为40次(每次旋转10°，另外增加45°、135°、225°、315°，旋转一周)记为与实验一对应的实验四，旋转测量次数达到40次时检测结果相对稳定，已经无限接近于真值。为了避免环境因素(如实验楼内人为因素引起的振动、气流等)引入的误差，实验测量选择在凌晨进行。

3 测量结果与数据分析

对3组实验的测量数据进行处理便可以分别得到3组平面1号、2号、3号的面型，如图3、图4、图5所示(从左到右依次为：实验一、实验二、实验三)。

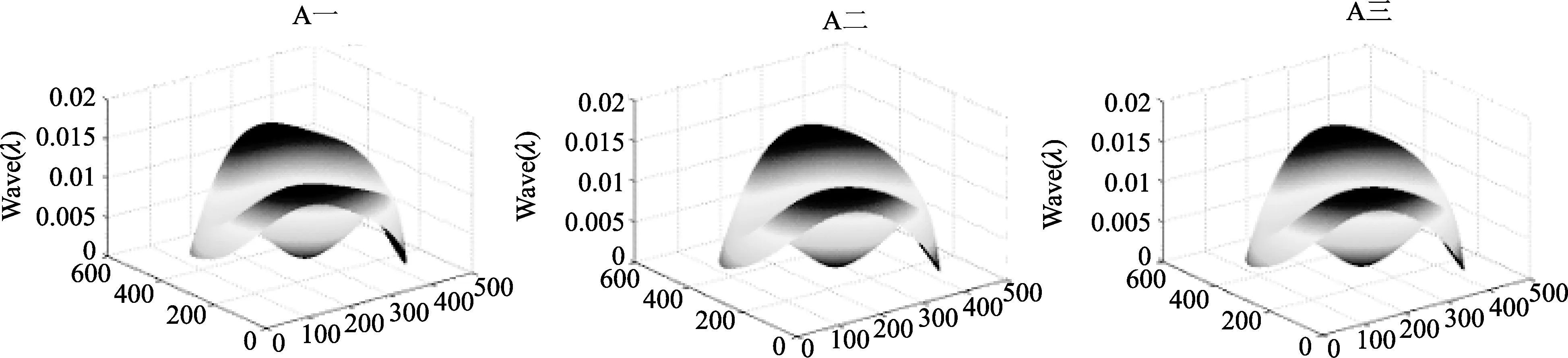
图3 3组实验得到的1号平面面型

图4 3组实验得到的2号平面面型

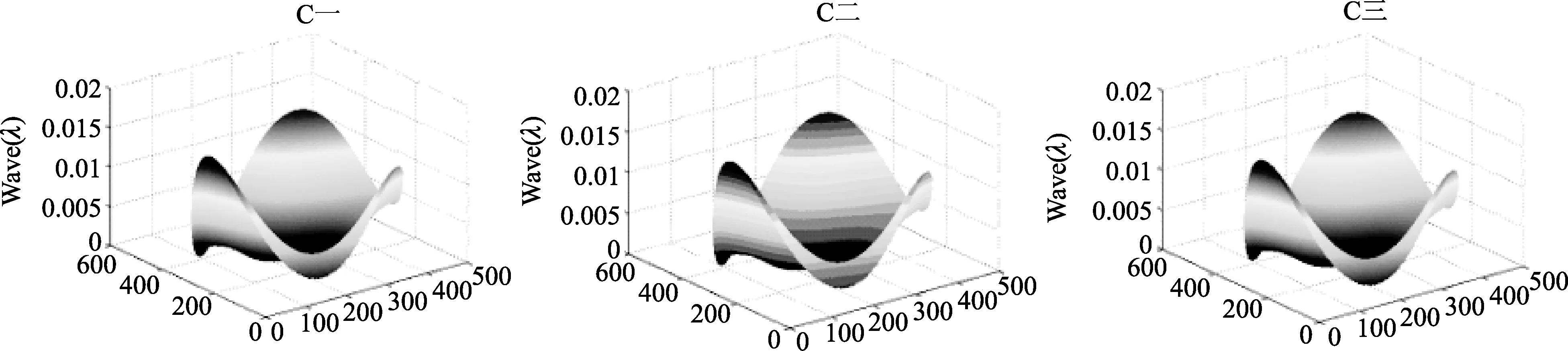
图5 3组实验得到的3号平面面型

为了定量的分析测量位置对最终检测结果的影响，分别令3组实验所得的1号平面的三维面型函数中x=(xmin+xmax)/2，3组实验所得的1号平面纵向面型比对如图6所示。

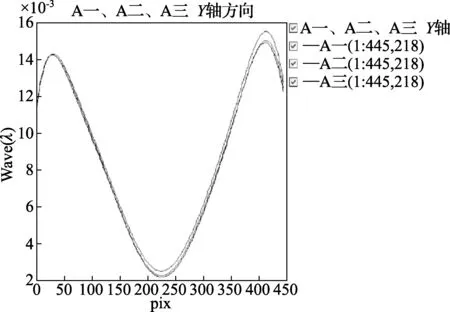
图6 3组实验所得1号平面纵向比对图

同理，3组实验所得的2号平面、3号平面纵向面型比对分别如图7、图8所示。

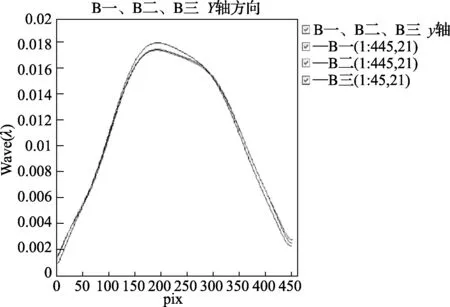
图7 3组实验所得2号平面纵向比对图

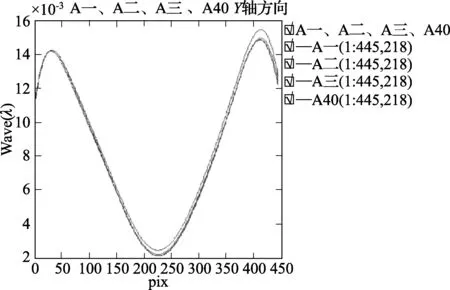
图8 3组实验所得3号平面纵向比对图

由图6、图7、图8可得：3条曲线相对的偏离量较大，但是当去除其中在实验中作为旋转平面的一个面所得的曲线时，对应的3组比对图中，每幅图中剩余2条曲线的最大偏离量，取它们中的最大值也仅为1.0360×10-4l。由于在实验二和实验三中1号平面均作为完全参考平面，其两条曲线的最大偏移量仅为5.4982×10-5l。为了进一步验证，我们将实验四(旋转测量次数为40次的实验一)所得1号平面纵向面型与其他3组实验所得1号平面纵向面型做比对，如图9所示(实验四结果已无限接近真值)。

图9 4组实验所得1号平面纵向比对图

由图9可得，再去除其中在实验中作为旋转平面的一个面所得的曲线的情况下，其他3条曲线的最大偏移量也仅为5.4982×10-5l。说明在旋转测量次数为8次的情况下做为完全参考面时其检测结果已经趋近于真值。

4 结论

通过对改进三平面互检法中，测量位置对最终检测结果影响的定量分析，结合已经研究的旋转测量次数对最终检测结果的影响，可知在改进三平面互检法实际检测过程中，3个测量位置对最终测量结果的影响由大到小依次为旋转平面、参考测试平面和完全参考面。且当测量次数为8次时，完全参考面位置的检测结果就可以达到无限接近真值(小于0.0001l)。

研究改进三平面互检法的初衷，就是为了对干涉测量中的参考面进行标定，且一般只需标定一个用于后续测量的参考面，所以这一结论就很有实际意义。在按照改进三平面互检法进行检测时，平面C安装在参考面位置进行最后2次测量后，改进三平面互检法测量结束。然后可以在平面C不动的情况下进行后续的干涉测量，这样既可以避免人为引入的其他误差，同时在对仪器旋转装置不提出很高要求的情况下(旋转测量次数为8次)，能起到对参考面的三维面型的精确标定，干涉法测量精度的进一步提高也就变为可能。

参考文献

[1] 田爱玲,郑显锋,刘丙才,王红军,王春慧,郑颖.三维面型的绝对测量[J].西安工业大学学报,2012(06)

[2] 郑显锋,郑颖,田爱玲.改进三平面互检法中旋转测量次数的定量分析[J].计量技术，2012(12)

[3] 徐晨,陈磊.光学平面绝对检验方法的研究[J].光学技术，2006,32(5):775-778

[4] M.F.Küchel.A new approach to solve the three flat problem[J].Optik 112，381-391(2001)

[5] Maurizio Vannoni and Giuseppe Molesini.Three-flat test with plates in horizontal posture[J].APPLIED OPTICS.28 March,2133-2145(2008)

[6] Maurizio Vannoni and Giuseppe Molesini.Absolute planarity with three-flat test：an iterative approach with Zernike polynomials[J].OPTICS EXPRESS.7 January .340-354(2008)

[7] UIf Griesmann,Quandou Wang,Johannes Soons.Three-flat tests including mounting-induced deformations[J].Optical Engineering，2007,46(9)：1-15