100μL移液器国际比对不确定度的分析与评定*

佟 林 王金涛 刘子勇 郭立功 暴雪松 赵晓惠

(中国计量科学研究院，北京 100013)

0 引言

移液器是具有一定量程范围，可将液体从容器内吸出，移入另一容器内的计量器具，作为量出式量器，分为定量和可调两种，广泛用于医院、输血站、生化实验室、环境实验室、制药实验室、食品等分析实验室的精密微量取样，可以对少量液体样品及试液进行迅速、准确的定量取样和加样。

随着医疗卫生、生物、制药、能源等领域的发展，微量移液器作为近几年的新产品，其加样更为精确，有利于提高实验的准确性与重复性，解决了大量分析试验中快速、准确微量取样的难题，替代了过去的玻璃吸管，在上述领域取得了广泛应用。据Global Industry Analysts发布的最新数据，亚太地区微量移液装置的增长率为5.7%，预计到2012年全球微量移液装置的市场将达到9.962亿美元，同时全球对移液器的保有量也在快速增长，这就要求世界各国对微量移液器的检定及校准能力要与国际接轨。

1 比对情况介绍

国际计量局(BIPM)流量计量工作组(WGFF)第10次年会于2010年10月在台湾举行。会议上，与会代表一致同意进行一次微小量的国际间比对。本次关键比对的目的在于，通过比对来检验各参比实验室对100μL移液器进行校准以及校准结果的一致性，及不同的测量设备和校准方法所带来的不确定度。

葡萄牙质量学会(IPQ)下属的容量实验室作为主导实验室，负责比对方案的确定、传递标准的选取、以及后续的数据分析等工作。中国计量科学研究院(NIM)以及墨西哥国家计量中心(CENAM)被选为副主导实验室，协助主导实验室进行比对安排，以及比对数据的整理及传递标准值的确定等相关工作。

参加本次国际关键比对的国家有：葡萄牙、南非、中国、墨西哥、巴西、英国、土耳其、法国、肯尼亚，比对过程中英国计量院退出，各参比实验室均采用静力称重法对移液器进行校准，比对采用环式路线进行，本次比对于2011年7月开始，并于2012年7月结束。

本次比对选用的传递标准是单头型定量移液器，如图1所示，共配备5支，编号分别为：354828Z、354853Z、354864Z、354868Z、354872Z。

图1 传递标准

2 用于微量容积值计算的数学模型

微量移液器是一种量出式计量器具，其校准方法主要有静力称重法、光度吸收法和滴定法等方法，其中一般以静力称重法的准确度最高。由于此次国际比对的量值为100μL，在这个量程静力称重法的优势比较明显，所以本次国际比对采用静力称重法进行微量液体容积值的测量,并换算成标准温度20℃下容积值，其数学模型为：

×[1-γ(t-20)]

(1)

式中：V20为修正到20℃下的容积值，μL；II为带液过渡容器质量值，mg；IE为过渡容器空称质量值，mg；ρW为实验温度下的水密度值，通过Tanaka公式计算[2]，mg/μL；ρA为空气密度，mg/μL；ρB为砝码密度，mg/μL；γ为移液器的热膨胀系数,2.4×10-4℃-1；t为实验过程中水温度，℃。

由于微量移液器作为活塞式量器，是通过活塞的移动产生负压和正压进行吸液及放液。即使活塞容积不发生变化，活塞内大气压强的变化也会导致在相同温度条件下移液器吸液量和排液量的不一致。这是由于微量移液器内部与外部气压不同从而产生压强差，而压强差又导致残留量和移液器虹吸现象的出现。通过修正后可以计算出液体的变化量。修正后的微量容积值计算模型为：

(2)

式中：Vt为活塞室容积，μL；g为重力加速度，m/s2；hw为吸液嘴中升高的液柱，m；pL,X1为X1中大气压强，Pa；pL,X2为X2中大气压强，Pa；ρw为X2中水密度，kg/m3。

3 不确定度评定

在测量过程中有许多影响因素成为了不确定度源，例如人为操作因素、仪器本身的不确定度、水的密度以及空气密度和大气压力等等，现以354828Z移液器为例，进行不确定度的分析。

3.1 标准不确定度的A类评定

按比对技术要求，对354828Z移液器，在同一条件下进行了10次独立的重复测量，得出其在标准温度20℃下的容积值，详见表1。

表1354828Z测量结果统计表

由贝塞尔公式求得测量值的实验标准差：

由测量重复性导致的测量结果的A类标准不确定度为：

3.2 标准不确定度的B类评定

3.2.1 水质量测量引入的不确定度分量u(M)

移液器排出的水质量是通过电子天平称量获得的，因此水质量测量B类不确定度取决于天平和砝码的测量误差，其中天平测量不确定度影响因素为灵敏度、分辨率和偏载，分别为us、ud和uE，砝码测量不确定度为uW，计算公式如下所示：

式中：us为电子天平的灵敏度,mg；ud为电子天平的分辨力,mg；uE为电子天平的偏载,mg。

=5.77×10-3mg

3.2.2 砝码密度引入的不确定度分量u(ρB)

砝码密度的测量误差为0.14g/cm3，(k=2)，所以：

u(ρB)=0.14/2=7.0×10-2g/cm3

3.2.3 空气密度引入的不确定度分量u(ρA)

按照CIPM推荐使用的空气密度计算公式，分析计算可以得到空气密度的测量的标准不确定度为：

u(ρA)=6.7×10-7g/cm3

3.2.4 水密度引入的不确定度分量u(ρW)

测量介质为去离子水，所以水密度采用了国际实用温标水密度值，其允差为±1×10-4g/cm3，服从均匀分布条件，其测量标准不确定度为：

3.2.5 移液器体胀系数引入的不确定度分量u(β)

移液器的热膨胀系数为2.4×10-4℃-1，根据经验值取u(β)=1.0×10-6℃-1。

3.2.6 水温度测量引入的不确定度分量u(t)

水温度测量误差为±0.01℃，考虑到水温梯度的影响，服从均匀分布条件，其测量标准不确定度为：

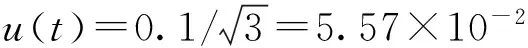
3.2.7 称量过程中水蒸发量引入的不确定度分量

移液器校准过程中，所排放水在称量时蒸发量按经验值取1.15×10-2μL。

通过对式(1)进行偏微分求导之后，得到B类不确定度分量：

=1.42×10-2μL

3.3 合成标准不确定度

上述不确定度评定方法仅仅适用于传递标准非常稳定的条件下，即传递标准本身的不确定度可以忽略。但是在测量中发现移液器(特别是微量移液器)受结构的影响性能不是足够的稳定，所以需要将传递标准不稳定性所引入的不确定度分量考虑在内。比对过程中，主导实验室在不同时间对作为传递标准的移液器进行了3次测量，以此来检验其在传递过程中的稳定性，同时也对移液器校准过程中操作方法[7](如移液器吸液嘴侵没深度、侵没角度、放液速度、放液角度等)进行了实验性研究，通过研究发现移液器自身结构所造成的最大允许误差能够达到±0.4%(Eexp)，因此需按式(3)计算新增的不确定度分量：

(3)

式中：s为主导实验室标准不确定度；n为主导实验室对同一支移液器校准次数，取n=3；Eexp为移液器最大允许误差，按经验值取Eexp=0.4%。

通过式(3)计算得出ust为0.13μL

所以，经过修正之后的合成标准不确定度计算方法为：

354828Z号移液器测量结果的不确定度分量汇总表如表2。

3.4 扩展不确定度

取k=2，则扩展不确定度：

4 比对结果分析

本次比对选用各参比实验室测量结果的加权平均值作为参考值，按式(4)计算。

(4)

此时加权算术平均值的标准不确定度按式(5)计算。

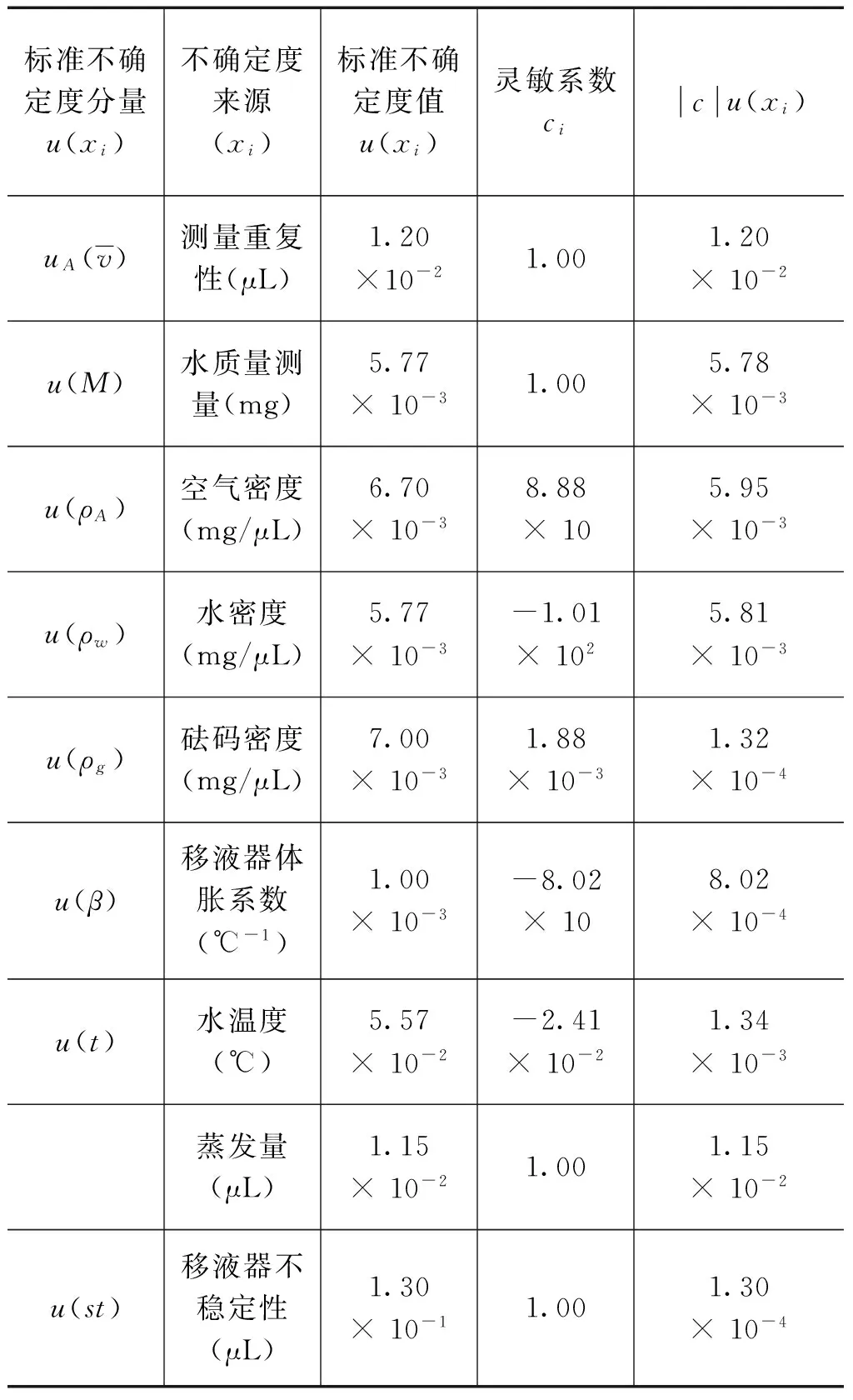
表2不确定度分量汇总表

(5)

通过计算得出参考值Y=100.03μL，加权算术平均值的标准不确定度uri=0.10μL。

比对结果采用比对判据En值进行评价，En值又称为归一化偏差，为各实验室比对结果与参考值的差值与该差值不确定度之比，其评判原则是：|En|≤1参比实验室测量结果与参考值之差在合理的预期范围之内，比对结果可以接受。

(6)

因各参比实验室测量结果相互无关，因此ui按式(7)计算：

(7)

通过以上公式可以得出NIM所提交的测量结果的En值为0.85，因此按评判原则，本次比对所提交的测量结果为有效比对值，如图2所示，同时也可以证明本次比对NIM所提交的校准数据是准确有效的。

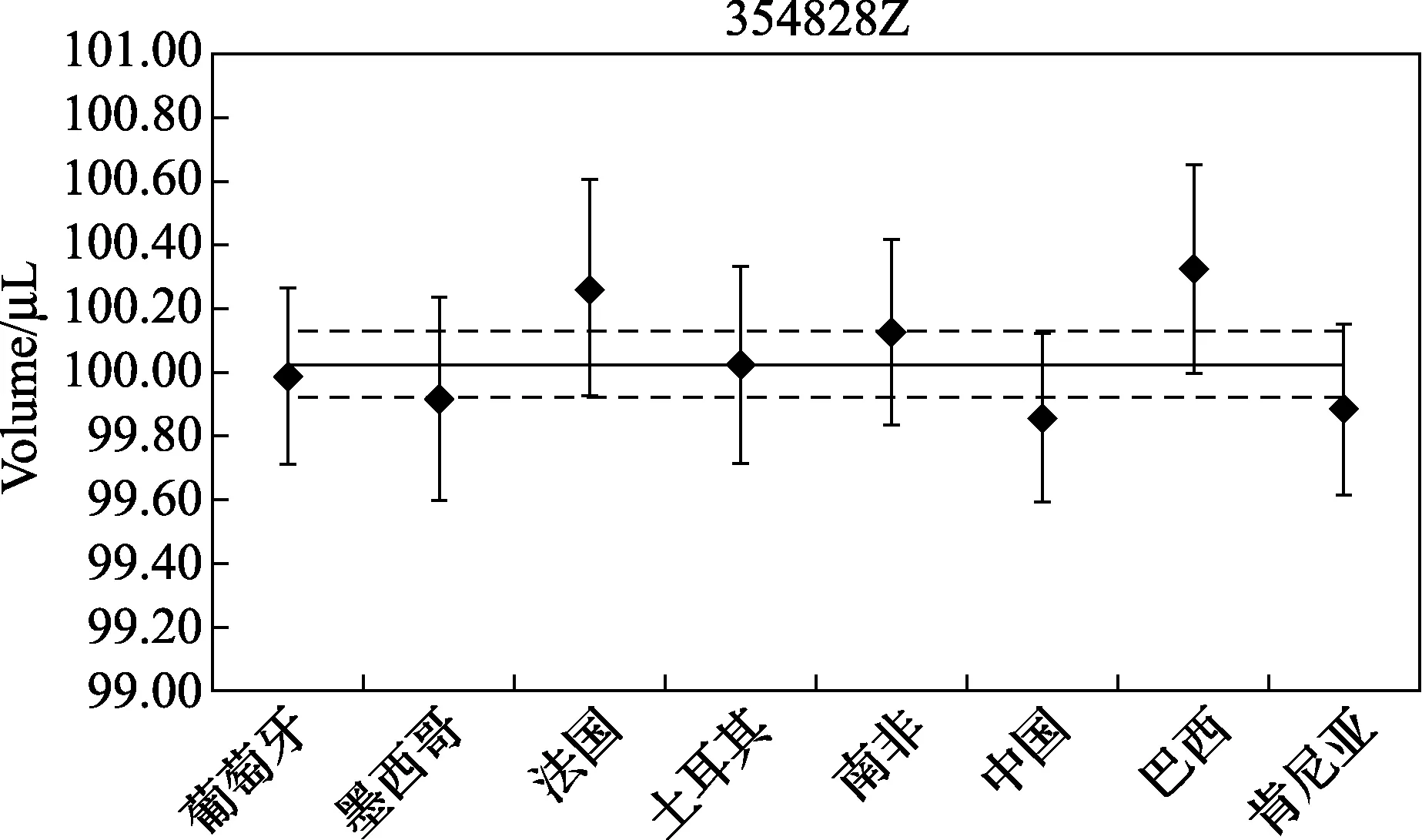
图2 比对结果汇总图

经过以上分析及计算之后，各参比实验室校准数据及扩展不确定度详见表3。

表3测量结果及不确定度汇总表

5 结束语

通过比对发现大气压力对移液器的校准结果有着较大影响，经过修正后各参比实验室的校准结果有了较好的一致性；同时经过对移液器的分析和数学模型的研究得出，由于其自身结构存在不稳定性所带入的不确定度分量是不确定度分析中的一个主要来源。本次比对证明用于微量容积值计算及不确定度分析的数学模型其算法准确、结果可靠，很好地解决了移液器在日常检定及校准中的数据处理问题。

[1] 刘子勇. 容量计量[M]. 北京:中国计量出版社，2009

[2] Tanaka, M., et. Al.Recommended table for the density of water between 0 ℃ and 40℃ based on recent experime ntal reports.Metrologia, 2001, 38：301-309

[3] ISO4787:2010 Laboratory glassware-Volumetric glassware-Methods for use and testing of capacity[S]

[4] ISO8655-1/2/6:2002 Piston-operated volumetric apparatus[S]

[5] S Lorefice.Traceability and uncertainty analysis in volume measurements[J]. Measurement，2009,42:1510-1515

[6] JJF 1059—1999 测量不确定度评定与表示[S]

[7] 佟林,王金涛,刘子勇. 移液器使用及校准过程中影响因素分析[J].中国计量，2012(5):79-81