基于卡尔曼滤波的OFDM系统时变信道估计方法
叶 磊
(中国地质大学 江城学院,湖北 武汉430074)
正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)作为一种多载波并行传输技术,具有高效的频谱利用率、优良的抗多径衰落能力和简单的系统硬件结构。OFDM以其多种优良性能成为无线通信系统最有竞争力的候选方案。
信道估计就是为了估计出信道的频域或者时域冲激响应,从而能大概率地恢复接收到的数据。在OFDM系统中,为了最大可能地保证信道的多径和衰落效应不会影响OFDM系统的性能,需要采用信道估计的方法逼近信道响应的随机变化,以便能用信道影响逆向修正信号。因此,寻找有效的信道估计算法已成为OFDM技术主要研究方向之一[1]。
现有的信道估计算法多数都假设信道是准静态的,即信道冲激响应在一个OFDM符号时间内基本不变或变化很慢,可以近似忽略。然而在高速移动环境下,多普勒频移扩展将导致信道在短时间内的冲激响应产生变化,使系统成为一个时变系统。无线信道上多普勒频移的存在使得信道特性具有时变性,给信道估计带来困难[2-3]。
Kalman滤波技术是一种可用于在线估计系统状态的方法,由量测值重构系统的状态向量,并以“预测-实测-修正”的顺序递推,根据系统的量测值来消除随机干扰,再现系统的状态。Kalman滤波用状态方程来描述状态变量的动态变化规律,并不需要知道全部过去的值,因此比较适用于时变系统。
目前,基于Kalman滤波方法的信道估计主要是半盲信道估计,整体算法过于复杂,均方误差和误码率还需提升,在实际应用中难以实现[4]。而利用导频可以进行信道随时间变化的跟踪[5],参考文献[6]基于导频的Kalman滤波方法用于信道子空间的跟踪,但频域估计部分直接求逆运算量也很庞大。
为了在性能和复杂度两方面做到很好的折衷,本文提出了一种基于导频的Kalman滤波的OFDM系统时变信道估计方法,通过独立跟踪每个子载波的接收信号,改善了信道估计 。仿真实验表明,本文针对OFDM系统时变信道估计策略,与基于导频的LS和MMSE算法相比,能够获得比传统系统更低的信道估计均方误差和误码率。
1 系统模型
假设OFDM系统的子载波数目为N,符号周期为T,设时变多径传播信道模型为[6]:

式中,h(t,τ)为信道冲激响应;gi(t)为第 i条路径的衰减系数;τi为第i条路径的传输延迟;L为路径数。
第n个OFDM符号的第k个子载波对应的信道冲激响应为:

式 中,gn=[gn,0gn,1… gn,L-1]T;τn=[τn,0τn,1… τn,L-1]T;Hn=[Hn(0)Hn(1)…Hn(N-1)]T。
发送序列x(n)经无线信道到达接收端,经快速FFT变换后,接收到第n个OFDM符号的第k个子载波输出可表示为:

式中,Wn(k)是系统观测零均值高斯白噪声,用来反映实际信道响应的变化。信道估计的目的是通过对发送信号和接收信号的分析选用合适的算法得到Hn(k)。例如,可通过梳状导频在N个子载波中插入Np个导频符号Xn,p(k)(k=0,1,…,Np-1),Xn,p(k)和 Yn,p(k)分别为发送信号和接收信号,则由式(3)可估计出信道响应 Hn,p(k)。
2 基于卡尔曼滤波的信道估计
采用Kalman滤波能跟踪时变信道,有利于对系统的分析与预测。取Hn为状态变量,而信道的时变特性可以用AR(Auto Regressive)模型来近似,在计算复杂度和精确度之间进行权衡,本文采用Hn模型为1阶,则第 n个OFDM符号的第k个子载波的状态空间模型可表示为(为了简洁省略序号k):
状态方程:

测量方程:

式中:Hn是系统在第n个OFDM符号的信道冲激响应;Vn为系统状态零均值高斯白噪声;Fn为状态转移矩阵。
用卡尔曼滤波来对Hn进行估计,首先根据以前的系统状态进行信道估计:

误差协方差矩阵预测为:

根据新的观测值来修正第一步的估计,产生新的估计,新估计误差为:

根据估计误差给出一种改善的状态估计:

式中,Kn为Kalman增益系数,可表示为:
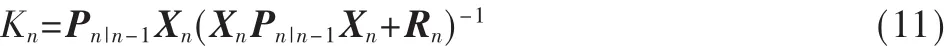
卡尔曼滤波是一种最优估计,由式(8)和式(9)可得到Hn的卡尔曼滤波估计值为:

式中,I为单位矩阵;Qn和 Rn分别为 Vn和 Wn的协方差矩阵。误差协方差矩阵Pn与测量数据无关,其初始值可设为 P0=I。
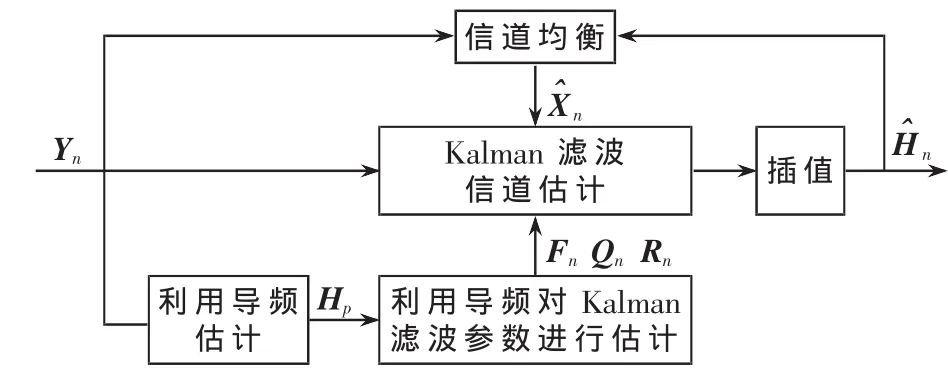
图1 基于Kalman滤波器的信道估计过程
Kalman滤波器的参数估计方法如下:
(1)参数Fn的估计。采用导频进行信道随时间变化的跟踪。假设子载波之间不相关,时变的状态转移矩阵Fn为:
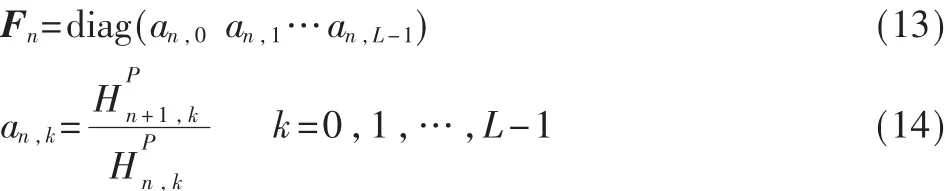
(2)参数Qn的估计。根据定义,Qn可表示为:

当子载波之间不相关时,第n个OFDM符号的第k个载波的频率响应过程噪声vn,k的方差为:

于是有:
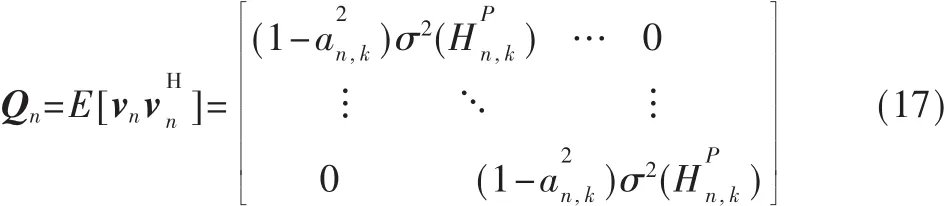
式中Qn为对角阵,)为H的方差,an,k可由式(14)计算而得。
(3)Rn的估计。当子载波之间不相关时,Rn为对角阵:
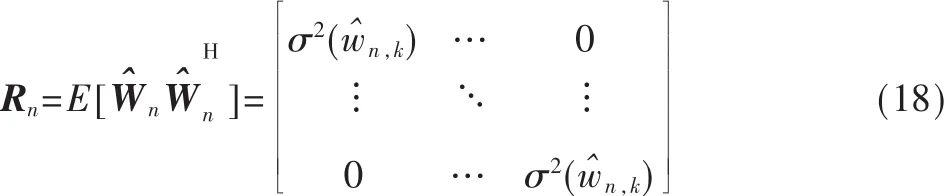
式中Wn的估计值为:

3 实验仿真与讨论
为了研究基于导频的Kalman滤波的时变信道估计方法在多径衰落信道中的性能,根据无线信道特性,仿真实验OFDM系统参数设置如表1所示。为了便于比较,采用基于导频的信道估计LS和MMSE算法。

表1 系统参数
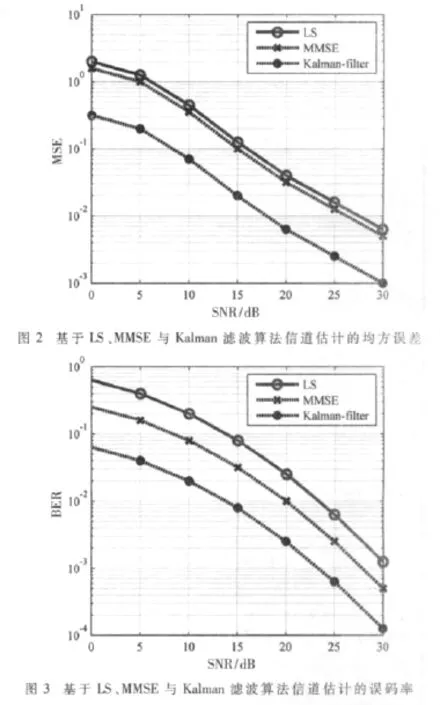
传统信道估计的算法主要包括LS、MMSE等。为了验证基于Kalman滤波的信道估计性能在时变多径信道上的优越性,首先比较传统算法 LS、MMSE和Kalman滤波算法在多径数为5的情况下,不同信噪比(SNR)的性能。3种算法的信道估计均方误差(MSE)和误码率(BER)分别如图2、图3所示。
图2为不同信噪比下,本文的Kalman滤波方法和传统的LS与MMSE算法相比得到的信道频率响应均方误差(MSE)的比较。相对于通常的LS与MMSE算法,MSE有较大的改善。在信噪比为0~30 dB时,均方误差下降一个数量级。这主要是因为Kalman滤波对估计误差进行计算,并对下一次的估计值进行调节,可以有效地跟踪时变信道。图3所示的误码率(BER)比较中,最大Doppler频移为132 Hz,可以看到本文的Kalman滤波方法与传统的LS和MMSE算法相比,在信噪比为0~30 dB时,误码率下降约一个数量级。这主要是因为Kalman滤波可以更好地跟踪信道的变化,同时对滤波结果在频域进行最小均方意义下的改进,进一步提高了性能。所以由图2、图3可以得出,在多径数为 5的情况下,由于基于Kalman滤波算法可以进行信道随时间变化的跟踪,所以表现出的性能也要比传统的算法要好。在此假设情况下,Kalman滤波的性能是一直优于LS与MMSE算法的。
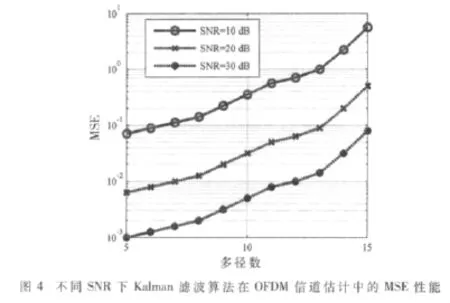
下面对基于导频的Kalman滤波进行不同多径(5~15)仿真分析,仿真的SNR范围是10 dB~30 dB,其他参数如表1所示。 并且假设循环前缀长度大于最大信道时延时间长度,也就是说,不存在符号间干扰。对于以下仿真,通过改变多径数来模拟该算法的性能。不考虑相位补偿、相位失调和载频补偿问题。
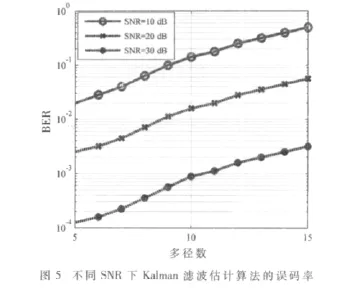
图4描述了Kalman滤波算法在OFDM信道估计中MSE的性能,多径数目变化范围为5~15,SNR范围为10 dB~30 dB。可以看出,随着多径数的增加,均方误差MSE也跟着增大。当OFDM系统包含适当的多径时,MSE的值是很低的。并且SNR的上升和下降,也影响MSE的值随之变化。图5是对不同信噪比下由Kalman滤波估计算法得到误码率的仿真。可以看出随着多径数目的增加,同一信噪比情况下,误码率呈现递增的趋势;不同SNR条件下的误码率呈现出不同程度的增长趋势。
本文基于OFDM系统为时变信道估计提出了卡尔曼滤波方法,该方法显著的特征是能对时变多径信道进行估计。根据信道的相关变化提出了监测状态变化的方法,经过仿真测试,表明所提出的卡尔曼滤波方法对时变多径信道估计方面有较好的结果。
[1]YANG B,LETAIEF K B,CHENG R S,et al.Channel estimation for OFDM transmission in multipath fading channels based on parametric channel modeling[J].IEEE Trans.on Communications,2001,49(3):467-478.
[2]HIJAZI H,ROS L.Rayleigh Time-varying channel complex gains estimation and ICI cancellation in OFDM systems[J].European Trans.on Telecommunications,2009,20(8):782-796.
[3]SHU F,LEE J,WU L N,et al.Time-frequency channel estimation for digital amplitude modulation broadcasting systems based on OFDM[J].IEE Proc.Communications,2003,150(4):259-264.
[4]赵康健,都思丹.基于多项式模型和卡尔曼滤波器的正交频分复用自适应信道估计算法[J].南京大学学报,2009,45(4):442-446.
[5]胡蝶,杨绿溪.OFDM系统中基于导频的时变信道估计[J].电子与信息学报,2004,26(9):1376-1382.
[6]HUANG M,CHEN X,XIAO L,et al.Kalman-filter-based channel estimation for orthogonal frequency-division multiplexing systems in time-varying channels[J].IET Communications,2007,1(4):795-801.

