FBAR传感器信号处理电路的设计*

秦 杰,杨 洋,熊 娟,顾豪爽

（湖北大学 物理学与电子技术学院,湖北 武汉430062）

近年来，随着射频无线通信技术和半导体工艺的迅猛发展，传统的传感器也正向微型化、智能化、信息化转变。以薄膜体声波谐振FBAR(Film Bulk Acoustic Wave)技术为基础的微质量传感器因其具有体积小、频率覆盖范围广、频带宽、Q值高、带外抑制高(大约 50 dB)、功率容量大、温度系数小、可与半导体工艺兼容等优势，显示出广阔的应用前景。

传统的FBAR质量传感器由FBAR器件和信号处理电路组成。在实际应用中，为了使微质量传感器方便使用，需要设计出一块包含了信号处理和信号数字量读取并输出的电路[1]。由于FBAR微质量传感器的信号频率为1GHz～2GHz甚至更高，普通的CMOS电路直接对该频率信号进行采集处理难度比较大，且难以保证精度。目前通常采用对频率信号先用N分频电路进行分频，使FBAR的输出频率降至CMOS电路可以处理的频率，再进行信号读取。本文采用双通道结构，模拟与数字相结合的方法进行信号的处理,先利用模拟电路进行信号的处理，再利用数字电路对处理过的信号进行周期或者频率的读取。

1 系统构成

根据Rayleigh理论,机电系统的谐振本质上是系统中动能和势能的平衡，在FBAR表面加载一定微扰量的物质后，原先的能量平衡被破坏，为了实现新的平衡，谐振频率必然降低，通过FBAR谐振频率的变化可以反推出加载在表面微扰量的大小。根据这个原理设计的信号处理电路结构如图1所示。该电路采用双通道结构，利用两个FBAR振荡器，其中一路作为参考，另外一路作为传感器吸附微小质量，由两个振荡频率的差值可推算得到微小质量的变化。采用差分的方式可以消除FBAR工作环境因素的不利影响，同时可靠性和检测精度也会得到提高[2]。

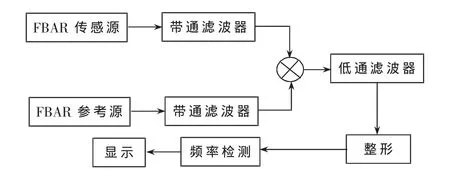
图1 FBAR微质量传感器信号处理电路原理框图

FBAR微质量传感电路由振荡、混频、滤波、波形整形、频率检测、显示六部分组成。在具体的设计中先利用正反馈原理，采用电容式反馈让FBAR起振,将质量变化的物理量转化为正弦频率的电信号，经过Motorola的MC1596混频器的混频，然后滤波，最后通过搭建的整形电路进行整形就可得到一个方波信号。频率检测是为了准确地检测这个方波信号的频率。

2 FPGA功能模块

在频率检测的模块中，以QuartusⅡ为开发工具，分别对频率检测的各个模块进行了VHDL描述。通过仿真验证其功能都得到了实现，最后的顶层设计仿真也说明频率检测是符合要求的。频率检测先把经过模拟电路处理好的信号送入量程选择模块，选择相应的档位，一路信号送入小数点产生模块，另外一路信号送入计数时钟和闸门产生模块；经过对石英晶振和被测信号的二分频产生计数时钟和闸门信号，再送入周期测量模块测出被测信号的周期，按照需要还可以把信号送入除法器得到频率；最后通过选择器来选择周期或者频率并送入相对应小数点的模块，最终送入显示模块。其电路框图如图2所示。

图2 频率检测模块电路框图

2.1 量程选择模块

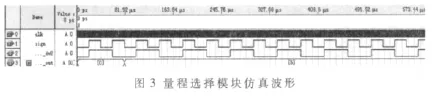
量程选择模块主要实现一个周期测量的计数器，用被测信号周期作为闸门的长度，用晶振时钟作为计数时钟，根据所记的数值来选择量程编号。该模块采用7位BCD计数器计数。把被测信号进行二分频然后送入到计数器的清零端，即可实现被测信号的二分频为低电平进行计数器计数,在被测信号的二分频为高电平时清零。7位BCD计数器主要输出2路信号，一个为进位信号count，另外一个为标志每一位 BCD数 zeros[6,0]是否为0,根据zeros[6,0]通过简单的组合逻辑译码电路即可选择量程编号。输出结果通过寄存器锁存，当计数器清零时，结果仍然保存在寄存器中。寄存器中的数据通过一个组合逻辑的译码电路显示出最终所需要的量程编号。

从图3所示仿真波形可见，当被测信号的频率为25 kHz时得到量程5，符合前面的分析。

2.2 时钟和闸门模块

时钟信号可能是晶振时钟或者晶振时钟的10分频，闸门信号可能是待测信号的 10分频、102分频、103分频、104分频、105分频、106分频。而闸门信号的分频问题可用量程估计模块所用的zeros[6,0]解决。例如zeros(2)代表7位BCD计数器的百位是否为0。假如要实现103分频，则 zeros(2)为高电平占 100个计数周期，zeros(2)为低电平占900个周期。时钟信号是晶振时钟或者晶振时钟的10分频，晶振时钟的10分频可通过1个模为10的计数器轻松实现。

时钟和闸门模块仿真波形如图4所示。图中被测信号的频率为 25 kHz,输出的时钟为10MHz，输出的闸门信号 gate宽度为 40ms。

2.3 周期计数模块

周期计数模块使用一个7位BCD计数来实现计数的稳定输出，采用2个寄存器来实现。通过前1个寄存器实现清零不锁存数据，后1个寄存器实现清零锁存数据[3]。最终实现了不输出中间计数结果、只稳定输出最终结果的目的。周期计数模块仿真波形如图5所示。

当闸门信号分别为100μs和10μs时，因为被测信号经过二分频才产生闸门信号，所以被测信号为 50μs和 5μs，图5中的相应的输出值为 49.9μs和 4.9μs，两者的误差都不大。

2.4 除法器模块

除法器模块的任务是周期到频率的转换。为了保证精度，决定输出结果也采用7位BCD数。这样被除数就需要达到1013。因为前面为了使计数都达到 106～107，闸门的宽度经过不同程度的分频，时间都在 0.1 s～1 s，除法器可以采用时序较慢的时序逻辑电路。这就意味着可以把除法运算转化成减法运算，相当于1013减去多少个闸门时间T[4]。因为高7位只是借位，实际发生变化的是低7位。因此，为了实现除法运算，需要一个7位减法器来运算低7位被除数减去除数T，需要一个减法计数器来保存被除数高7位BCD数，还需要一个7位 BCD加法器来保存做过的减法运算的次数。除法器的结构框图如图6所示。

这里还涉及了一个状态转换，于是采用了状态机这个概念。状态机相当于一个电路控制系统，负责寄存器的被除数和除数的加载、清零以及计数器的清零和计数等功能[5]。状态s0表示就绪状态，负责各个寄存器和计数器的清零和加载。s0持续一个晶振周期后自动转换到s1。在s1状态下，做减法运算，直到 7位 BCD减法计数器为0，代表被除数高7位全部借完，此时状态s1结束，转为状态s2，即把7位 BCD加法器的结果输出到寄存器B。

图7所示为除法器的仿真波形。可以看到，状态机先从001(s0)经过1个周期的等待无条件地转换到 010(s1)；当zeros产生高电平，即借位完毕时再转换到100(s2)并输出结果。

2.5 小数点模块

由于精度的要求，改变了闸门的大小，使读数始终保持 106～107，这就需要小数模块来实现读数的准确化。因为假如读数都是4×106，如果没有小数点的选择，将不知道这个数到底表示多大的周期或者频率。小数点的显示与量程的选择其实是一一对应的。例如0.01μs，小数点控制位显示0000100。在周期模式里，小数对应方式为：量程0对应0000001，量程 1对应 0000010，量程 2对应 0000100，量程3对应0001000，量程4对应0010000，量程5对应0100000，量程 6对应 1000000，量程 7对应 1111111。 在频率模式下，小数对应方式为：量程 0对应1111111，量程 1对应 1000000，量程 2对应 0100000，量程 3对应0010000，量程 4对应 0001000，量程 5对应 0000100，量程6对应0000010，量程7对应0000001。小数点仿真波形如图8所示。

最后把所有的模块连接起来，可实现对顶层设计的仿真，仿真波形如图9所示。

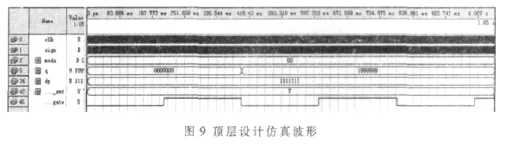
由图可知，5MHz的被测信号的周期为 0.2 s,实验所得为 0.199 999 9s，相对误差为 1×10-6。

本设计通过模拟电路和数字电路的结合，实现了微质量传感器把质量向频率的转换，并能准确地显示出该信号的频率或者周期。通过对所设计的电路的仿真和实验，验证了其可行性。

[1]王振红.VHDL与数字电路设计与应用实践教程[M].北京：机械工业出版社，2006.

[2]王永良,宋政湘.基于FPGA的同步测周期高精度数字频率计的设计[J].电子设计应用，2004(12):74-76.

[3]骆舒萍.基于 QuartusⅡ软件平台的八位数字频率计设计[J].漯河职业技术学院学报，2011,10(2):20-23.

[4]杨守良.基于FPGA的数字频率计的设计和实现[J].现代电子技术，2005(11):118-120.

[5]刘昌华.数字逻辑EDA设计与实践[M].北京：国防工业出版社，2006.