基于SAD算法的立体匹配的实现*

岳陈平,孟丽娅

(重庆大学 光电工程学院，重庆400030)

立体视觉理论的提出和美国MIT的Robert完成的三维景物分析工作把过去的二维图像分析推广到了三维景物[1]。利用立体视觉来恢复物体的三维立体信息可以应用在工业自动化生产线等检测领域，如产品检测、工业探伤、PCB印制板检查以及各种危险场合工作的机器人等。而一个完整的立体视觉系统的核心工作就是立体匹配。立体匹配算法需要处理大量复杂数据，采用PC来实现数据的快速处理不仅会占用CPU的大量时间，而且在功耗方面也难以承受。而利用现场可编程门阵列FPGA(Field Programmable Gate Array)等硬件的方法来进行立体视觉的研究，有益于实现系统的实时性并降低功耗。本文采用FPGA，利用补码实现SAD匹配算法，基于窗口并行和像素串行完成匹配算法的流程，这种算法流程不仅效果好、速度快，而且具有较强的鲁棒性，很适合采用硬件方式来实现。

1 立体匹配算法

立体匹配算法中基于区域匹配的算法其性能在很大程度上要依赖于相似性测度因子的选取，而最常用的测度因子有像素灰度差的绝对值和SAD(Sum of Absolute Differences)、像素灰度差的平方和SSD (Sum of Squared Differences)、归一化相关方法NCC(Normalized Cross Correlation)[2]。SSD算法有平方运算，NCC有除法和开方的运算，而SAD只有加法运算，从算法的复杂度和硬件实现的难易度来看，SSD和NCC将会占用FPGA大量的逻辑单元并且耗时量大。SAD算法表达式为[3]：

其中，disp为左摄像机拍摄的图像上窗口在外极线上移动的距离，即视差；PL(i，j)表示基准图中的待匹配像素的灰度值，PR(i，j)表示配准图中的匹配点的灰度值。计算不同视差情况下的SAD值，选取SAD的最小值，此时，PR为PL点在配准图中的最佳匹配点。

在常规的算法中，绝对值AD为:

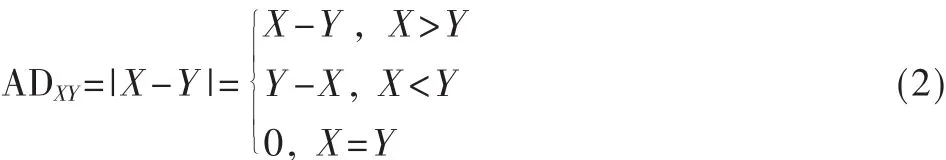
在硬件实现中，用这种方法来求取绝对值会耗费较多的FPGA逻辑单元，如图1所示。其中，MSB为选择器MUX 的判断信号，当 X＞Y 时，MSB=0，此时，AD＝X-Y;相反时,AD＝Y-X。

为了减少FPGA的逻辑单元使用率，采用补码来计算 X、Y的绝对值，即：

在求绝对值过程中，如果X＞Y，则MSB=0；相反，MSB=1，ADXY的取值为X-Y的补码,硬件实现过程如图2所示。

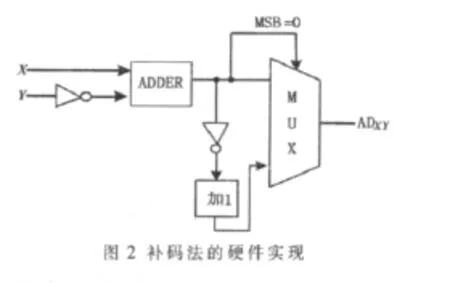
2 算法流程及硬件实现

2.1 算法流程

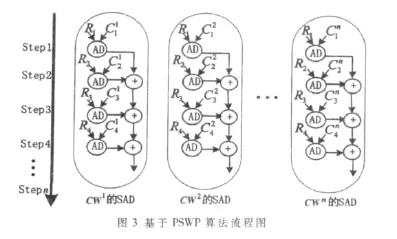
为了能够实现快速实时的图像处理，硬件结构通常选择并行操作来实现具有高效率和实时性的图像处理算法。立体匹配算法有像素并行运算 (pixel-parallel)和窗口并行运算 (window-parallel)[2-3]两种。在硬件资源的约束下，像素并行运算方式只适用于窗口大小固定的立体匹配，窗口大小可变以及要考虑硬件资源的利用率时，像素并行运算方法就不适用。因此，在一般的硬件实现立体匹配运算中，为了获得高效率的匹配值，这两种并行结构可适当地结合使用或是有选择地使用。当把两种并行结构结合起来运算时，可以分为像素并行和窗口串行PPWS(Pixel-Parallel and Window-Serial)以及像素串行和窗口并行PSWP(Pixel-Serial and Window-Parallel)[4-5]。综合考虑，本文中采用了图3所示的PSWP算法流程。图3中共有n个匹配窗口，CWn表示第n个匹配窗口，Ri表示基准图中匹配窗口的像素值，C表示配准图中第n个匹配窗口中的像素值，AD表示求取两个像素值绝对值差，在每个窗口中采用像素值串行的运算方式,并同时计算n个窗口的数据。

2.2 硬件实现

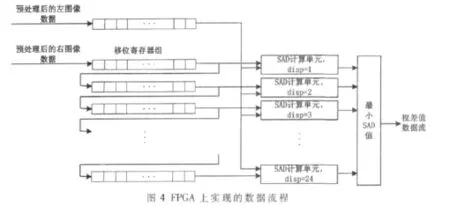
利用FPGA实现立体匹配算法。设计的关键在于，在片内RAM带宽和容量制约的前提下，充分利用FPGA并行性计算和合理的流水线设计来实现并行计算，并且能够把算法直接映射到结构上[6]。在FPGA上实现的具体流程如图4所示。将采集到的图像数据首先经过图像的中值滤波预处理，左图像数据经过缓存单元输送至SAD计算单元，右图数据输送到由FIFO构成的移位寄存器组，通过移位寄存器组后，在控制单元的作用下与左图像缓存后的数据同时输送到SAD计算单元，在SAD计算单元计算不同视差值情况下的SAD值，经比较得出最小的SAD值，输出最小SAD值所对应的视差值。

采用Altera公司的Stratix系列EP2S15F672C3器件，利用Verilog HDL语言编写了程序代码，并且在QUARTUS II和Modelsim 6.0中进行功能和时序仿真。本文以图像大小128×128为例，窗口大小设置为3×3，视差为 24，通过对算法的简化，实现SAD算法。所需的资源如表1所示。图5所示为最后的结果图。表2为本算法与其他算法性能对比。

表1 SAD算法所需要的资源

本文完成了一个基于FPGA实现立体匹配的算法过程，结合硬件结构的存储和资源的限制，在实现SAD算法过程中采用了并行计算和流水线结构，并且在具体的运算中选取了PSWP的运算流程。本方案共消耗该系列FPGA 3 620个逻辑单元，约相当于总数的29%；消耗FPGA内部容量为263 424 bit，约为总容量的63%。将本文方案与其他方案进行比较，由于采用的匹配算法不同，获得的视差图也是不同的，因此直接比较每个方案占用的逻辑单元来判断帧率的大小是不可取的，但是可得到这样的结论：在简化算法和合理地采用并行流水线结构的条件下,选择SAD算法运用硬件方法来实现匹配比用软件方法更胜一筹。因此，在搭建一个低功耗的立体视觉系统时，FPGA器件是最佳的选择。

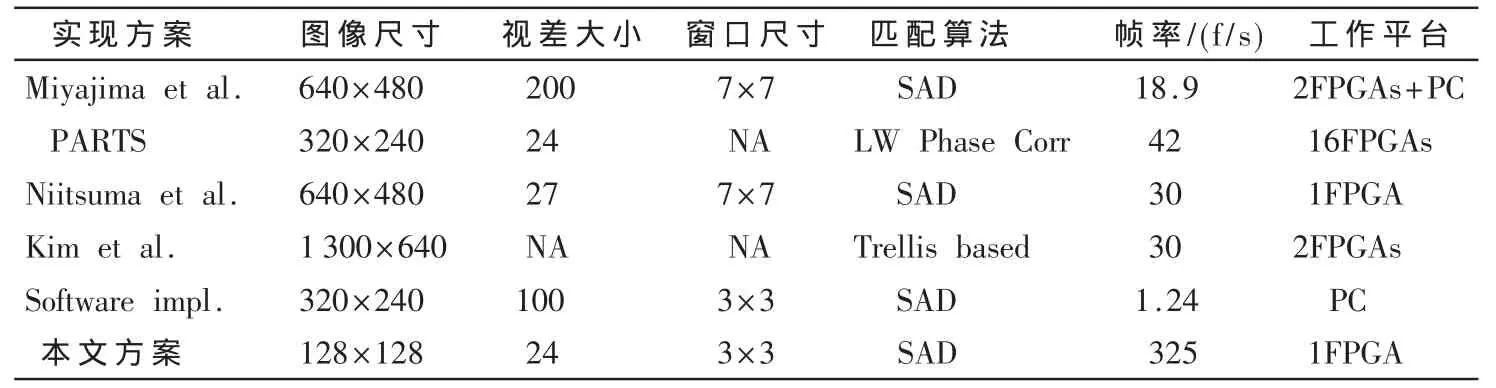
表2 不同匹配方案的比较

[1]STEGER C，ULRICH M，WIEDEMANN C.机器视觉算法与应用[M].杨少荣,等译.北京:清华大学出版社，2008.

[2]MARR D.视觉计算理论[M].姚国正，刘磊，汪云久,译.北京:科技出版社，1998.

[3]AMBROSCH K,HUMENBERGER M,KUBINGER W,et al.Hardware implementation of an SAD based stereo vision algorithm[C].Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops,Minneapolis,2007:1-6.

[4]CHEN L,Jia Yunde.A parallel reconfigurable architecture for real-time stereo vision[C].Proceedings of the International Conference on Embedded Software and Systems,2009:32-39.

[5]HARIYAMA M,KAMEYAMA M.VLSI Processor for Reliable stereo matching based on window-parallel logic-inmemory architecture[C].Proceedings of the Symp on VLSI Circuits Digital of Technology Papers,2004.

[6]HARIYAMA M,YOKOYAMA N,KAMEYAMA M,et al.FPGA implemetation of a stereo matching processor basedon window-parallel-and-pixel-parallel architecture[C].Proceedings of the IEEE Int.Midwest Symp.on Circ.And Syst,2005.(收稿日期：2012-12-20)